Noise-conditioned Energy-based Annealed Rewards (NEAR): A Generative Framework for Imitation Learning from Observation

This paper introduces a new imitation learning framework based on energy-based generative models capable of learning complex, physics-dependent, robot motion policies through state-only expert motion trajectories. Our algorithm, called Noise-conditioned Energy-based Annealed Rewards (NEAR), constructs several perturbed versions of the expert's motion data distribution and learns smooth, and well-defined representations of the data distribution's energy function using denoising score matching. We propose to use these learnt energy functions as reward functions to learn imitation policies via reinforcement learning. We also present a strategy to gradually switch between the learnt energy functions, ensuring that the learnt rewards are always well-defined in the manifold of policy-generated samples. We evaluate our algorithm on complex humanoid tasks such as locomotion and martial arts and compare it with state-only adversarial imitation learning algorithms like Adversarial Motion Priors (AMP). Our framework sidesteps the optimisation challenges of adversarial imitation learning techniques and produces results comparable to AMP in several quantitative metrics across multiple imitation settings.

Grasp Diffusion Network: Learning Grasp Generators from Partial Point Clouds with Diffusion Models in SO(3)xR3

Grasping objects successfully from a single-view camera is crucial in many robot manipulation tasks. An approach to solve this problem is to leverage simulation to create large datasets of pairs of objects and grasp poses, and then learn a conditional generative model that can be prompted quickly during deployment. However, the grasp pose data is highly multimodal since there are several ways to grasp an object. Hence, in this work, we learn a grasp generative model with diffusion models to sample candidate grasp poses given a partial point cloud of an object. A novel aspect of our method is to consider diffusion in the manifold space of rotations and to propose a collision-avoidance cost guidance to improve the grasp success rate during inference. To accelerate grasp sampling we use recent techniques from the diffusion literature to achieve faster inference times. We show in simulation and real-world experiments that our approach can grasp several objects from raw depth images with $90\%$ success rate and benchmark it against several baselines.

Global Tensor Motion Planning

Batch planning is increasingly crucial for the scalability of robotics tasks and dataset generation diversity. This paper presents Global Tensor Motion Planning (GTMP) -- a sampling-based motion planning algorithm comprising only tensor operations. We introduce a novel discretization structure represented as a random multipartite graph, enabling efficient vectorized sampling, collision checking, and search. We provide an early theoretical investigation showing that GTMP exhibits probabilistic completeness while supporting modern GPU/TPU. Additionally, by incorporating smooth structures into the multipartite graph, GTMP directly plans smooth splines without requiring gradient-based optimization. Experiments on lidar-scanned occupancy maps and the MotionBenchMarker dataset demonstrate GTMP's computation efficiency in batch planning compared to baselines, underscoring GTMP's potential as a robust, scalable planner for diverse applications and large-scale robot learning tasks.

ActionFlow: Equivariant, Accurate, and Efficient Policies with Spatially Symmetric Flow Matching

Spatial understanding is a critical aspect of most robotic tasks, particularly when generalization is important. Despite the impressive results of deep generative models in complex manipulation tasks, the absence of a representation that encodes intricate spatial relationships between observations and actions often limits spatial generalization, necessitating large amounts of demonstrations. To tackle this problem, we introduce a novel policy class, ActionFlow. ActionFlow integrates spatial symmetry inductive biases while generating expressive action sequences. On the representation level, ActionFlow introduces an SE(3) Invariant Transformer architecture, which enables informed spatial reasoning based on the relative SE(3) poses between observations and actions. For action generation, ActionFlow leverages Flow Matching, a state-of-the-art deep generative model known for generating high-quality samples with fast inference - an essential property for feedback control. In combination, ActionFlow policies exhibit strong spatial and locality biases and SE(3)-equivariant action generation. Our experiments demonstrate the effectiveness of ActionFlow and its two main components on several simulated and real-world robotic manipulation tasks and confirm that we can obtain equivariant, accurate, and efficient policies with spatially symmetric flow matching. Project website: https://flowbasedpolicies.github.io/

Deep Generative Models in Robotics: A Survey on Learning from Multimodal Demonstrations

Learning from Demonstrations, the field that proposes to learn robot behavior models from data, is gaining popularity with the emergence of deep generative models. Although the problem has been studied for years under names such as Imitation Learning, Behavioral Cloning, or Inverse Reinforcement Learning, classical methods have relied on models that don't capture complex data distributions well or don't scale well to large numbers of demonstrations. In recent years, the robot learning community has shown increasing interest in using deep generative models to capture the complexity of large datasets. In this survey, we aim to provide a unified and comprehensive review of the last year's progress in the use of deep generative models in robotics. We present the different types of models that the community has explored, such as energy-based models, diffusion models, action value maps, or generative adversarial networks. We also present the different types of applications in which deep generative models have been used, from grasp generation to trajectory generation or cost learning. One of the most important elements of generative models is the generalization out of distributions. In our survey, we review the different decisions the community has made to improve the generalization of the learned models. Finally, we highlight the research challenges and propose a number of future directions for learning deep generative models in robotics.

PianoMime: Learning a Generalist, Dexterous Piano Player from Internet Demonstrations

In this work, we introduce PianoMime, a framework for training a piano-playing agent using internet demonstrations. The internet is a promising source of large-scale demonstrations for training our robot agents. In particular, for the case of piano-playing, Youtube is full of videos of professional pianists playing a wide myriad of songs. In our work, we leverage these demonstrations to learn a generalist piano-playing agent capable of playing any arbitrary song. Our framework is divided into three parts: a data preparation phase to extract the informative features from the Youtube videos, a policy learning phase to train song-specific expert policies from the demonstrations and a policy distillation phase to distil the policies into a single generalist agent. We explore different policy designs to represent the agent and evaluate the influence of the amount of training data on the generalization capability of the agent to novel songs not available in the dataset. We show that we are able to learn a policy with up to 56\% F1 score on unseen songs.

Hierarchical Policy Blending as Inference for Reactive Robot Control

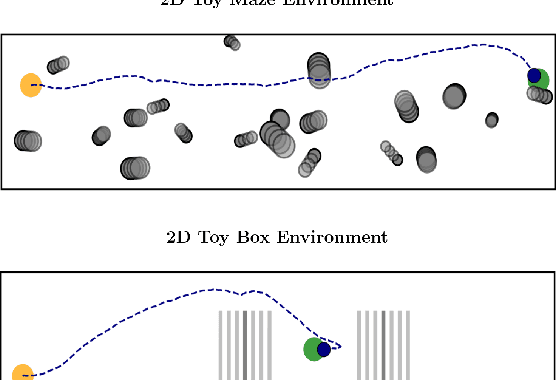
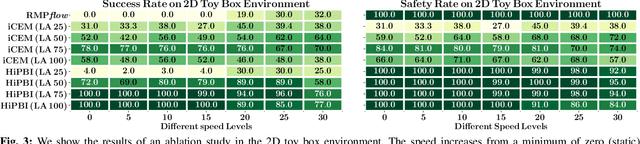
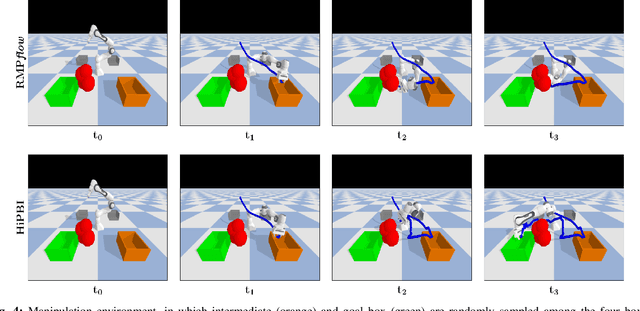
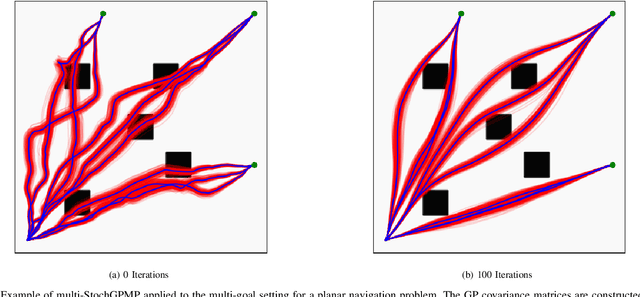
Motion generation in cluttered, dense, and dynamic environments is a central topic in robotics, rendered as a multi-objective decision-making problem. Current approaches trade-off between safety and performance. On the one hand, reactive policies guarantee fast response to environmental changes at the risk of suboptimal behavior. On the other hand, planning-based motion generation provides feasible trajectories, but the high computational cost may limit the control frequency and thus safety. To combine the benefits of reactive policies and planning, we propose a hierarchical motion generation method. Moreover, we adopt probabilistic inference methods to formalize the hierarchical model and stochastic optimization. We realize this approach as a weighted product of stochastic, reactive expert policies, where planning is used to adaptively compute the optimal weights over the task horizon. This stochastic optimization avoids local optima and proposes feasible reactive plans that find paths in cluttered and dense environments. Our extensive experimental study in planar navigation and 6DoF manipulation shows that our proposed hierarchical motion generation method outperforms both myopic reactive controllers and online re-planning methods.

SE(3)-DiffusionFields: Learning smooth cost functions for joint grasp and motion optimization through diffusion

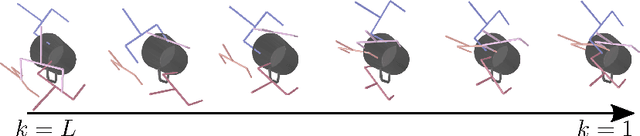
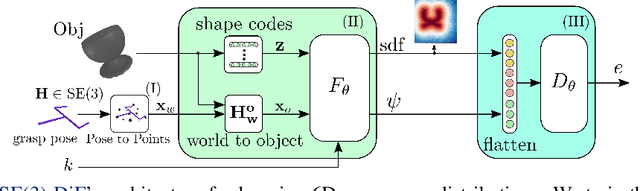
Multi-objective optimization problems are ubiquitous in robotics, e.g., the optimization of a robot manipulation task requires a joint consideration of grasp pose configurations, collisions and joint limits. While some demands can be easily hand-designed, e.g., the smoothness of a trajectory, several task-specific objectives need to be learned from data. This work introduces a method for learning data-driven SE(3) cost functions as diffusion models. Diffusion models can represent highly-expressive multimodal distributions and exhibit proper gradients over the entire space due to their score-matching training objective. Learning costs as diffusion models allows their seamless integration with other costs into a single differentiable objective function, enabling joint gradient-based motion optimization. In this work, we focus on learning SE(3) diffusion models for 6DoF grasping, giving rise to a novel framework for joint grasp and motion optimization without needing to decouple grasp selection from trajectory generation. We evaluate the representation power of our SE(3) diffusion models w.r.t. classical generative models, and we showcase the superior performance of our proposed optimization framework in a series of simulated and real-world robotic manipulation tasks against representative baselines.

Learning Implicit Priors for Motion Optimization

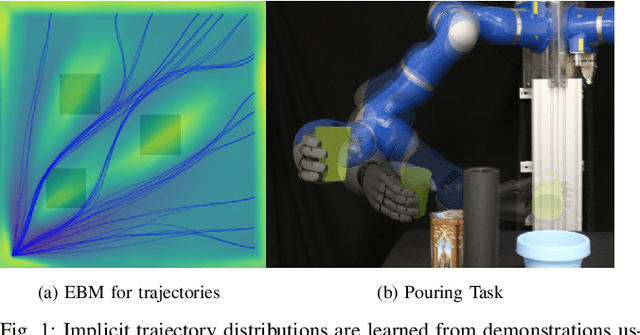
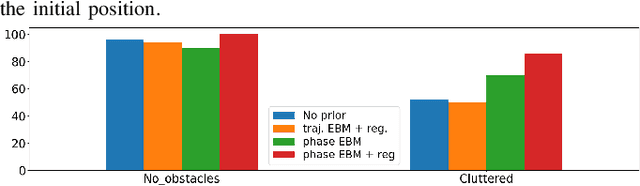
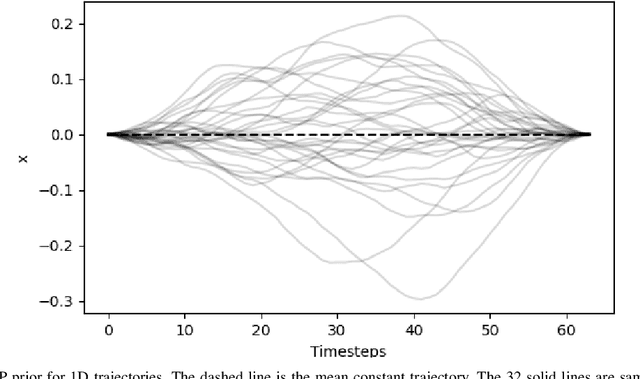
In this paper, we focus on the problem of integrating Energy-based Models (EBM) as guiding priors for motion optimization. EBMs are a set of neural networks that can represent expressive probability density distributions in terms of a Gibbs distribution parameterized by a suitable energy function. Due to their implicit nature, they can easily be integrated as optimization factors or as initial sampling distributions in the motion optimization problem, making them good candidates to integrate data-driven priors in the motion optimization problem. In this work, we present a set of required modeling and algorithmic choices to adapt EBMs into motion optimization. We investigate the benefit of including additional regularizers in the learning of the EBMs to use them with gradient-based optimizers and we present a set of EBM architectures to learn generalizable distributions for manipulation tasks. We present multiple cases in which the EBM could be integrated for motion optimization and evaluate the performance of learned EBMs as guiding priors for both simulated and real robot experiments.

A Hierarchical Approach to Active Pose Estimation

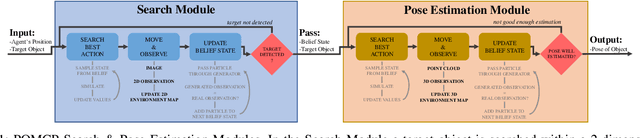
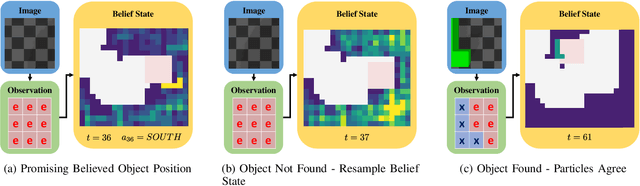
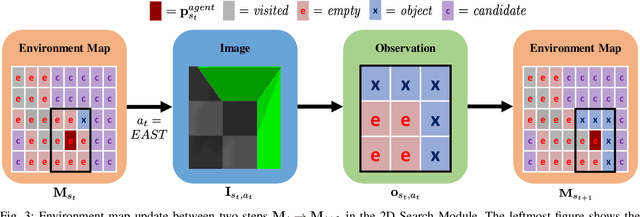
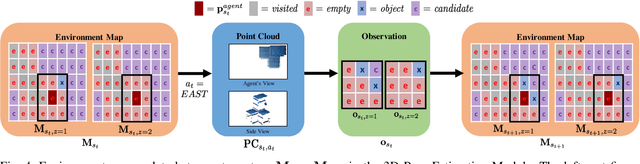
Creating mobile robots which are able to find and manipulate objects in large environments is an active topic of research. These robots not only need to be capable of searching for specific objects but also to estimate their poses often relying on environment observations, which is even more difficult in the presence of occlusions. Therefore, to tackle this problem we propose a simple hierarchical approach to estimate the pose of a desired object. An Active Visual Search module operating with RGB images first obtains a rough estimation of the object 2D pose, followed by a more computationally expensive Active Pose Estimation module using point cloud data. We empirically show that processing image features to obtain a richer observation speeds up the search and pose estimation computations, in comparison to a binary decision that indicates whether the object is or not in the current image.