Language Models and Cycle Consistency for Self-Reflective Machine Translation

This paper introduces a novel framework that leverages large language models (LLMs) for machine translation (MT). We start with one conjecture: an ideal translation should contain complete and accurate information for a strong enough LLM to recover the original sentence. We generate multiple translation candidates from a source language A to a target language B, and subsequently translate these candidates back to the original language A. By evaluating the cycle consistency between the original and back-translated sentences using metrics such as token-level precision and accuracy, we implicitly estimate the translation quality in language B, without knowing its ground-truth. This also helps to evaluate the LLM translation capability, only with monolingual corpora. For each source sentence, we identify the translation candidate with optimal cycle consistency with the original sentence as the final answer. Our experiments demonstrate that larger LLMs, or the same LLM with more forward passes during inference, exhibit increased cycle consistency, aligning with the LLM model size scaling law and test-time computation scaling law. This work provide methods for, 1) to implicitly evaluate translation quality of a sentence in the target language, 2), to evaluate capability of LLM for any-to-any-language translation, and 3), how to generate a better translation for a specific LLM.

Deep Nonparametric Convexified Filtering for Computational Photography, Image Synthesis and Adversarial Defense

We aim to provide a general framework of for computational photography that recovers the real scene from imperfect images, via the Deep Nonparametric Convexified Filtering (DNCF). It is consists of a nonparametric deep network to resemble the physical equations behind the image formation, such as denoising, super-resolution, inpainting, and flash. DNCF has no parameterization dependent on training data, therefore has a strong generalization and robustness to adversarial image manipulation. During inference, we also encourage the network parameters to be nonnegative and create a bi-convex function on the input and parameters, and this adapts to second-order optimization algorithms with insufficient running time, having 10X acceleration over Deep Image Prior. With these tools, we empirically verify its capability to defend image classification deep networks against adversary attack algorithms in real-time.

Relay Diffusion: Unifying diffusion process across resolutions for image synthesis

Diffusion models achieved great success in image synthesis, but still face challenges in high-resolution generation. Through the lens of discrete cosine transformation, we find the main reason is that \emph{the same noise level on a higher resolution results in a higher Signal-to-Noise Ratio in the frequency domain}. In this work, we present Relay Diffusion Model (RDM), which transfers a low-resolution image or noise into an equivalent high-resolution one for diffusion model via blurring diffusion and block noise. Therefore, the diffusion process can continue seamlessly in any new resolution or model without restarting from pure noise or low-resolution conditioning. RDM achieves state-of-the-art FID on CelebA-HQ and sFID on ImageNet 256$\times$256, surpassing previous works such as ADM, LDM and DiT by a large margin. All the codes and checkpoints are open-sourced at \url{https://github.com/THUDM/RelayDiffusion}.

Robust Boosting Forests with Richer Deep Feature Hierarchy

We propose a robust variant of boosting forest to the various adversarial defense methods, and apply it to enhance the robustness of the deep neural network. We retain the deep network architecture, weights, and middle layer features, then install gradient boosting forest to select the features from each layer of the deep network, and predict the target. For training each decision tree, we propose a novel conservative and greedy trade-off, with consideration for less misprediction instead of pure gain functions, therefore being suboptimal and conservative. We actively increase tree depth to remedy the accuracy with splits in more features, being more greedy in growing tree depth. We propose a new task on 3D face model, whose robustness has not been carefully studied, despite the great security and privacy concerns related to face analytics. We tried a simple attack method on a pure convolutional neural network (CNN) face shape estimator, making it degenerate to only output average face shape with invisible perturbation. Our conservative-greedy boosting forest (CGBF) on face landmark datasets showed a great improvement over original pure deep learning methods under the adversarial attacks.

Quantized Adaptive Subgradient Algorithms and Their Applications

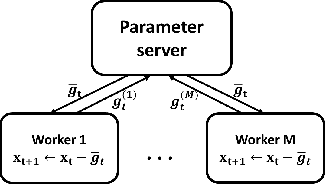
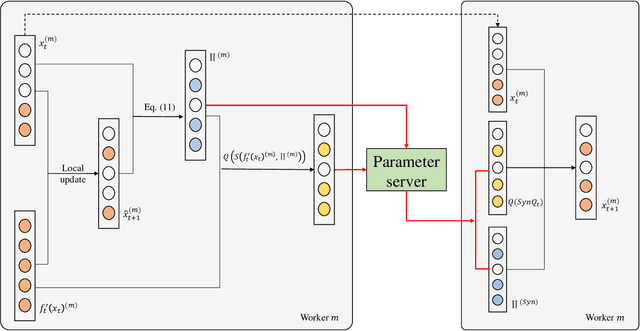
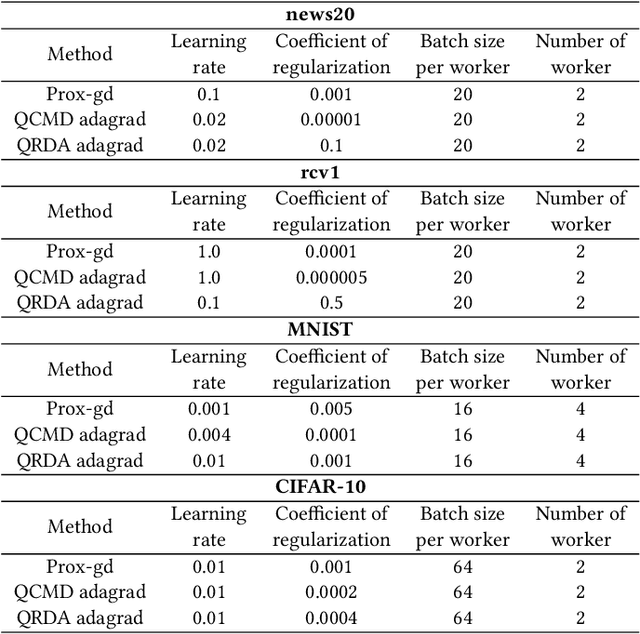
Data explosion and an increase in model size drive the remarkable advances in large-scale machine learning, but also make model training time-consuming and model storage difficult. To address the above issues in the distributed model training setting which has high computation efficiency and less device limitation, there are still two main difficulties. On one hand, the communication costs for exchanging information, e.g., stochastic gradients among different workers, is a key bottleneck for distributed training efficiency. On the other hand, less parameter model is easy for storage and communication, but the risk of damaging the model performance. To balance the communication costs, model capacity and model performance simultaneously, we propose quantized composite mirror descent adaptive subgradient (QCMD adagrad) and quantized regularized dual average adaptive subgradient (QRDA adagrad) for distributed training. To be specific, we explore the combination of gradient quantization and sparse model to reduce the communication cost per iteration in distributed training. A quantized gradient-based adaptive learning rate matrix is constructed to achieve a balance between communication costs, accuracy, and model sparsity. Moreover, we theoretically find that a large quantization error brings in extra noise, which influences the convergence and sparsity of the model. Therefore, a threshold quantization strategy with a relatively small error is adopted in QCMD adagrad and QRDA adagrad to improve the signal-to-noise ratio and preserve the sparsity of the model. Both theoretical analyses and empirical results demonstrate the efficacy and efficiency of the proposed algorithms.

Normalized Diversification

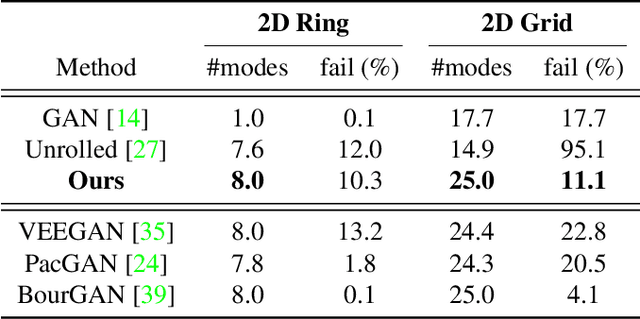
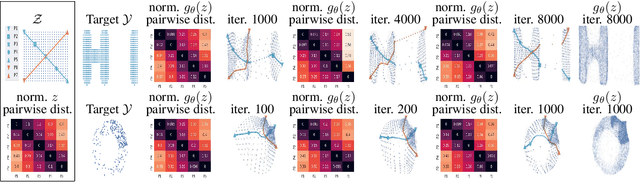
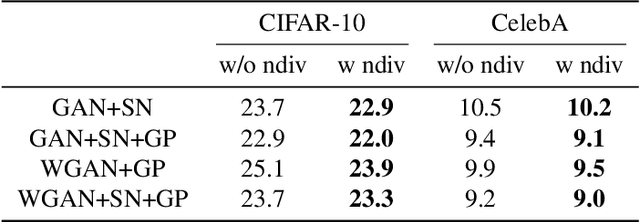
Generating diverse yet specific data is the goal of the generative adversarial network (GAN), but it suffers from the problem of mode collapse. We introduce the concept of normalized diversity which force the model to preserve the normalized pairwise distance between the sparse samples from a latent parametric distribution and their corresponding high-dimensional outputs. The normalized diversification aims to unfold the manifold of unknown topology and non-uniform distribution, which leads to safe interpolation between valid latent variables. By alternating the maximization over the pairwise distance and updating the total distance (normalizer), we encourage the model to actively explore in the high-dimensional output space. We demonstrate that by combining the normalized diversity loss and the adversarial loss, we generate diverse data without suffering from mode collapsing. Experimental results show that our method achieves consistent improvement on unsupervised image generation, conditional image generation and hand pose estimation over strong baselines.

Trajectory Normalized Gradients for Distributed Optimization

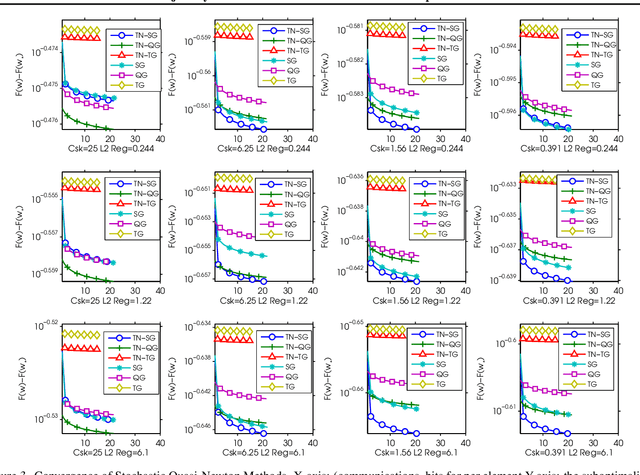
Recently, researchers proposed various low-precision gradient compression, for efficient communication in large-scale distributed optimization. Based on these work, we try to reduce the communication complexity from a new direction. We pursue an ideal bijective mapping between two spaces of gradient distribution, so that the mapped gradient carries greater information entropy after the compression. In our setting, all servers should share a reference gradient in advance, and they communicate via the normalized gradients, which are the subtraction or quotient, between current gradients and the reference. To obtain a reference vector that yields a stronger signal-to-noise ratio, dynamically in each iteration, we extract and fuse information from the past trajectory in hindsight, and search for an optimal reference for compression. We name this to be the trajectory-based normalized gradients (TNG). It bridges the research from different societies, like coding, optimization, systems, and learning. It is easy to implement and can universally combine with existing algorithms. Our experiments on benchmarking hard non-convex functions, convex problems like logistic regression demonstrate that TNG is more compression-efficient for communication of distributed optimization of general functions.

Monocular 3D Pose Recovery via Nonconvex Sparsity with Theoretical Analysis

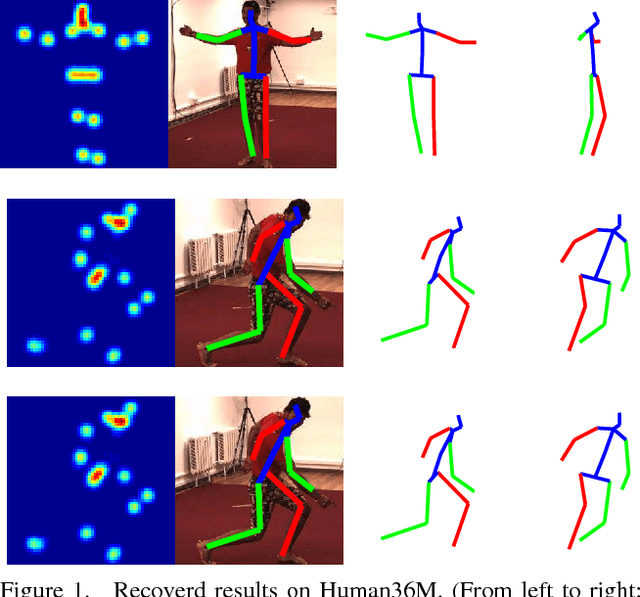
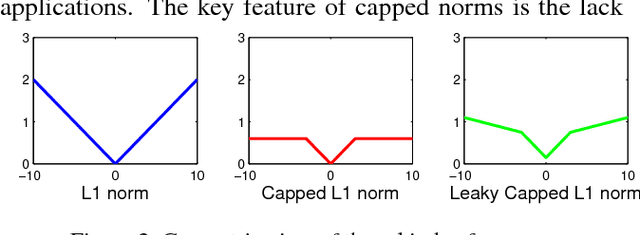
For recovering 3D object poses from 2D images, a prevalent method is to pre-train an over-complete dictionary $\mathcal D=\{B_i\}_i^D$ of 3D basis poses. During testing, the detected 2D pose $Y$ is matched to dictionary by $Y \approx \sum_i M_i B_i$ where $\{M_i\}_i^D=\{c_i \Pi R_i\}$, by estimating the rotation $R_i$, projection $\Pi$ and sparse combination coefficients $c \in \mathbb R_{+}^D$. In this paper, we propose non-convex regularization $H(c)$ to learn coefficients $c$, including novel leaky capped $\ell_1$-norm regularization (LCNR), \begin{align*} H(c)=\alpha \sum_{i } \min(|c_i|,\tau)+ \beta \sum_{i } \max(| c_i|,\tau), \end{align*} where $0\leq \beta \leq \alpha$ and $0<\tau$ is a certain threshold, so the invalid components smaller than $\tau$ are composed with larger regularization and other valid components with smaller regularization. We propose a multi-stage optimizer with convex relaxation and ADMM. We prove that the estimation error $\mathcal L(l)$ decays w.r.t. the stages $l$, \begin{align*} Pr\left(\mathcal L(l) < \rho^{l-1} \mathcal L(0) + \delta \right) \geq 1- \epsilon, \end{align*} where $0< \rho <1, 0<\delta, 0<\epsilon \ll 1$. Experiments on large 3D human datasets like H36M are conducted to support our improvement upon previous approaches. To the best of our knowledge, this is the first theoretical analysis in this line of research, to understand how the recovery error is affected by fundamental factors, e.g. dictionary size, observation noises, optimization times. We characterize the trade-off between speed and accuracy towards real-time inference in applications.

Training L1-Regularized Models with Orthant-Wise Passive Descent Algorithms

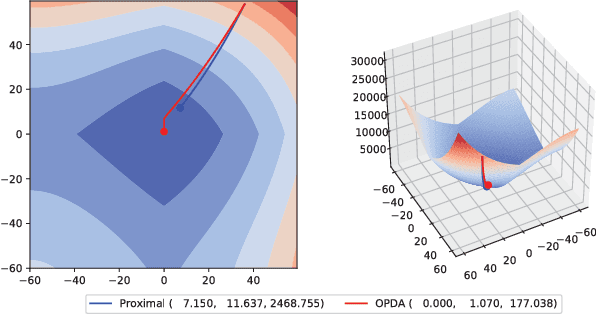
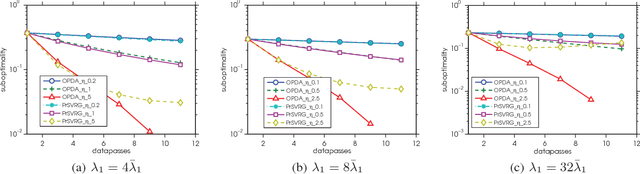
The $L_1$-regularized models are widely used for sparse regression or classification tasks. In this paper, we propose the orthant-wise passive descent algorithm (OPDA) for optimizing $L_1$-regularized models, as an improved substitute of proximal algorithms, which are the standard tools for optimizing the models nowadays. OPDA uses a stochastic variance-reduced gradient (SVRG) to initialize the descent direction, then apply a novel alignment operator to encourage each element keeping the same sign after one iteration of update, so the parameter remains in the same orthant as before. It also explicitly suppresses the magnitude of each element to impose sparsity. The quasi-Newton update can be utilized to incorporate curvature information and accelerate the speed. We prove a linear convergence rate for OPDA on general smooth and strongly-convex loss functions. By conducting experiments on $L_1$-regularized logistic regression and convolutional neural networks, we show that OPDA outperforms state-of-the-art stochastic proximal algorithms, implying a wide range of applications in training sparse models.

Learning Random Fourier Features by Hybrid Constrained Optimization

The kernel embedding algorithm is an important component for adapting kernel methods to large datasets. Since the algorithm consumes a major computation cost in the testing phase, we propose a novel teacher-learner framework of learning computation-efficient kernel embeddings from specific data. In the framework, the high-precision embeddings (teacher) transfer the data information to the computation-efficient kernel embeddings (learner). We jointly select informative embedding functions and pursue an orthogonal transformation between two embeddings. We propose a novel approach of constrained variational expectation maximization (CVEM), where the alternate direction method of multiplier (ADMM) is applied over a nonconvex domain in the maximization step. We also propose two specific formulations based on the prevalent Random Fourier Feature (RFF), the masked and blocked version of Computation-Efficient RFF (CERF), by imposing a random binary mask or a block structure on the transformation matrix. By empirical studies of several applications on different real-world datasets, we demonstrate that the CERF significantly improves the performance of kernel methods upon the RFF, under certain arithmetic operation requirements, and suitable for structured matrix multiplication in Fastfood type algorithms.