Frontier Language Models are not Robust to Adversarial Arithmetic, or "What do I need to say so you agree 2+2=5?

We introduce and study the problem of adversarial arithmetic, which provides a simple yet challenging testbed for language model alignment. This problem is comprised of arithmetic questions posed in natural language, with an arbitrary adversarial string inserted before the question is complete. Even in the simple setting of 1-digit addition problems, it is easy to find adversarial prompts that make all tested models (including PaLM2, GPT4, Claude2) misbehave, and even to steer models to a particular wrong answer. We additionally provide a simple algorithm for finding successful attacks by querying those same models, which we name "prompt inversion rejection sampling" (PIRS). We finally show that models can be partially hardened against these attacks via reinforcement learning and via agentic constitutional loops. However, we were not able to make a language model fully robust against adversarial arithmetic attacks.

Small-scale proxies for large-scale Transformer training instabilities

Teams that have trained large Transformer-based models have reported training instabilities at large scale that did not appear when training with the same hyperparameters at smaller scales. Although the causes of such instabilities are of scientific interest, the amount of resources required to reproduce them has made investigation difficult. In this work, we seek ways to reproduce and study training stability and instability at smaller scales. First, we focus on two sources of training instability described in previous work: the growth of logits in attention layers (Dehghani et al., 2023) and divergence of the output logits from the log probabilities (Chowdhery et al., 2022). By measuring the relationship between learning rate and loss across scales, we show that these instabilities also appear in small models when training at high learning rates, and that mitigations previously employed at large scales are equally effective in this regime. This prompts us to investigate the extent to which other known optimizer and model interventions influence the sensitivity of the final loss to changes in the learning rate. To this end, we study methods such as warm-up, weight decay, and the $\mu$Param (Yang et al., 2022), and combine techniques to train small models that achieve similar losses across orders of magnitude of learning rate variation. Finally, to conclude our exploration we study two cases where instabilities can be predicted before they emerge by examining the scaling behavior of model activation and gradient norms.

Dueling Decoders: Regularizing Variational Autoencoder Latent Spaces

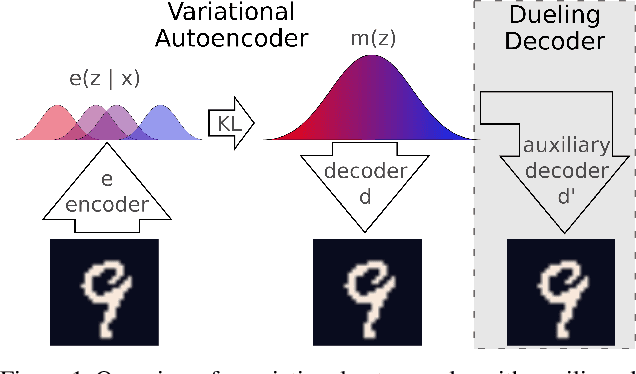
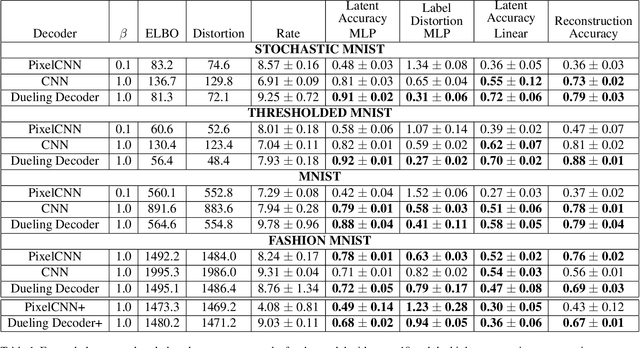
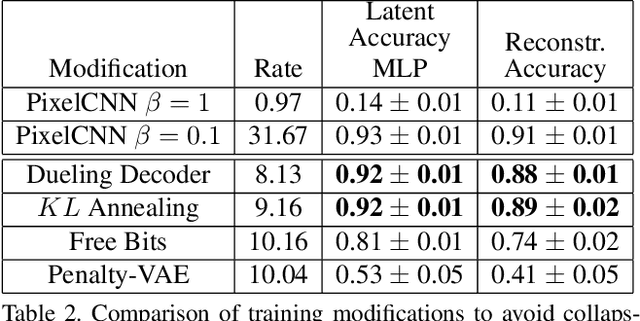
Variational autoencoders learn unsupervised data representations, but these models frequently converge to minima that fail to preserve meaningful semantic information. For example, variational autoencoders with autoregressive decoders often collapse into autodecoders, where they learn to ignore the encoder input. In this work, we demonstrate that adding an auxiliary decoder to regularize the latent space can prevent this collapse, but successful auxiliary decoding tasks are domain dependent. Auxiliary decoders can increase the amount of semantic information encoded in the latent space and visible in the reconstructions. The semantic information in the variational autoencoder's representation is only weakly correlated with its rate, distortion, or evidence lower bound. Compared to other popular strategies that modify the training objective, our regularization of the latent space generally increased the semantic information content.

Watch Your Step: Learning Node Embeddings via Graph Attention

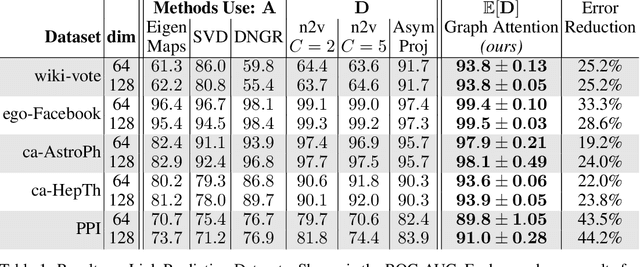
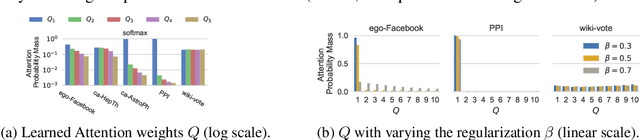
Graph embedding methods represent nodes in a continuous vector space, preserving information from the graph (e.g. by sampling random walks). There are many hyper-parameters to these methods (such as random walk length) which have to be manually tuned for every graph. In this paper, we replace random walk hyper-parameters with trainable parameters that we automatically learn via backpropagation. In particular, we learn a novel attention model on the power series of the transition matrix, which guides the random walk to optimize an upstream objective. Unlike previous approaches to attention models, the method that we propose utilizes attention parameters exclusively on the data (e.g. on the random walk), and not used by the model for inference. We experiment on link prediction tasks, as we aim to produce embeddings that best-preserve the graph structure, generalizing to unseen information. We improve state-of-the-art on a comprehensive suite of real world datasets including social, collaboration, and biological networks. Adding attention to random walks can reduce the error by 20% to 45% on datasets we attempted. Further, our learned attention parameters are different for every graph, and our automatically-found values agree with the optimal choice of hyper-parameter if we manually tune existing methods.

TensorFlow Distributions

The TensorFlow Distributions library implements a vision of probability theory adapted to the modern deep-learning paradigm of end-to-end differentiable computation. Building on two basic abstractions, it offers flexible building blocks for probabilistic computation. Distributions provide fast, numerically stable methods for generating samples and computing statistics, e.g., log density. Bijectors provide composable volume-tracking transformations with automatic caching. Together these enable modular construction of high dimensional distributions and transformations not possible with previous libraries (e.g., pixelCNNs, autoregressive flows, and reversible residual networks). They are the workhorse behind deep probabilistic programming systems like Edward and empower fast black-box inference in probabilistic models built on deep-network components. TensorFlow Distributions has proven an important part of the TensorFlow toolkit within Google and in the broader deep learning community.

Motion Prediction Under Multimodality with Conditional Stochastic Networks

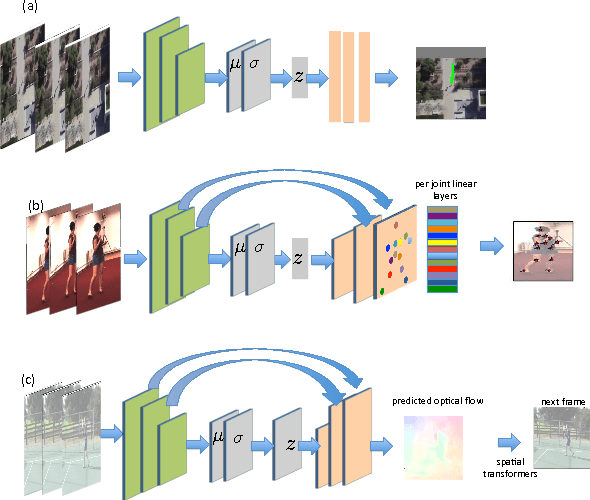
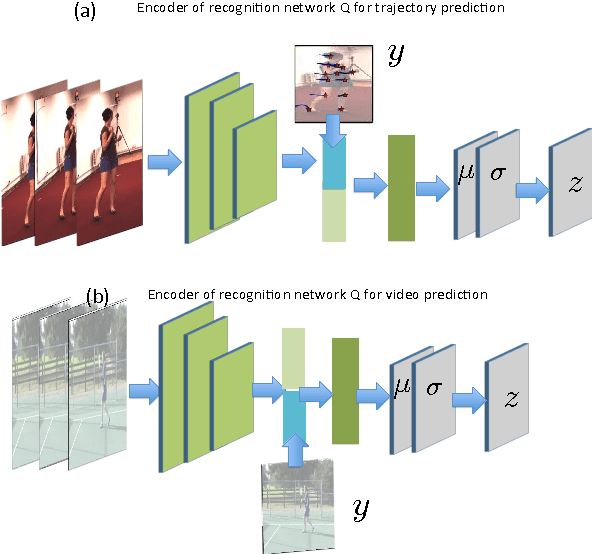
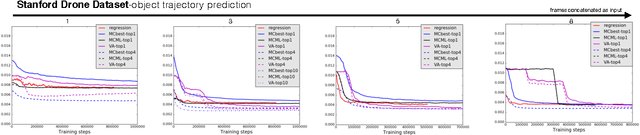
Given a visual history, multiple future outcomes for a video scene are equally probable, in other words, the distribution of future outcomes has multiple modes. Multimodality is notoriously hard to handle by standard regressors or classifiers: the former regress to the mean and the latter discretize a continuous high dimensional output space. In this work, we present stochastic neural network architectures that handle such multimodality through stochasticity: future trajectories of objects, body joints or frames are represented as deep, non-linear transformations of random (as opposed to deterministic) variables. Such random variables are sampled from simple Gaussian distributions whose means and variances are parametrized by the output of convolutional encoders over the visual history. We introduce novel convolutional architectures for predicting future body joint trajectories that outperform fully connected alternatives \cite{DBLP:journals/corr/WalkerDGH16}. We introduce stochastic spatial transformers through optical flow warping for predicting future frames, which outperform their deterministic equivalents \cite{DBLP:journals/corr/PatrauceanHC15}. Training stochastic networks involves an intractable marginalization over stochastic variables. We compare various training schemes that handle such marginalization through a) straightforward sampling from the prior, b) conditional variational autoencoders \cite{NIPS2015_5775,DBLP:journals/corr/WalkerDGH16}, and, c) a proposed K-best-sample loss that penalizes the best prediction under a fixed "prediction budget". We show experimental results on object trajectory prediction, human body joint trajectory prediction and video prediction under varying future uncertainty, validating quantitatively and qualitatively our architectural choices and training schemes.

Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning

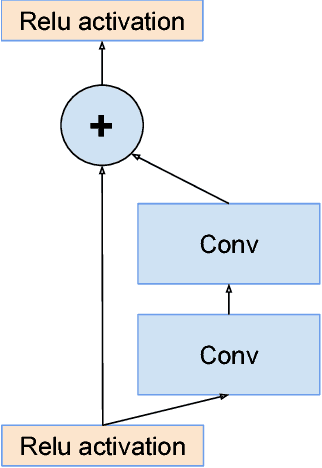
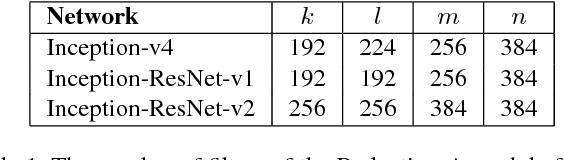
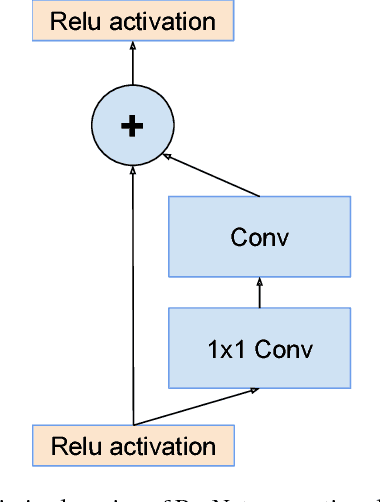
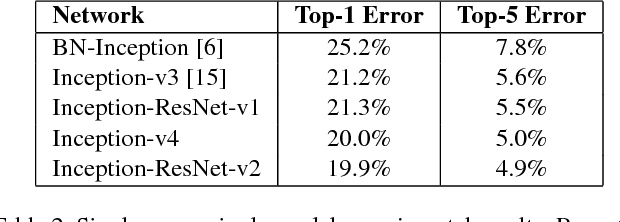
Very deep convolutional networks have been central to the largest advances in image recognition performance in recent years. One example is the Inception architecture that has been shown to achieve very good performance at relatively low computational cost. Recently, the introduction of residual connections in conjunction with a more traditional architecture has yielded state-of-the-art performance in the 2015 ILSVRC challenge; its performance was similar to the latest generation Inception-v3 network. This raises the question of whether there are any benefit in combining the Inception architecture with residual connections. Here we give clear empirical evidence that training with residual connections accelerates the training of Inception networks significantly. There is also some evidence of residual Inception networks outperforming similarly expensive Inception networks without residual connections by a thin margin. We also present several new streamlined architectures for both residual and non-residual Inception networks. These variations improve the single-frame recognition performance on the ILSVRC 2012 classification task significantly. We further demonstrate how proper activation scaling stabilizes the training of very wide residual Inception networks. With an ensemble of three residual and one Inception-v4, we achieve 3.08 percent top-5 error on the test set of the ImageNet classification (CLS) challenge