sbi reloaded: a toolkit for simulation-based inference workflows

Scientists and engineers use simulators to model empirically observed phenomena. However, tuning the parameters of a simulator to ensure its outputs match observed data presents a significant challenge. Simulation-based inference (SBI) addresses this by enabling Bayesian inference for simulators, identifying parameters that match observed data and align with prior knowledge. Unlike traditional Bayesian inference, SBI only needs access to simulations from the model and does not require evaluations of the likelihood-function. In addition, SBI algorithms do not require gradients through the simulator, allow for massive parallelization of simulations, and can perform inference for different observations without further simulations or training, thereby amortizing inference. Over the past years, we have developed, maintained, and extended $\texttt{sbi}$, a PyTorch-based package that implements Bayesian SBI algorithms based on neural networks. The $\texttt{sbi}$ toolkit implements a wide range of inference methods, neural network architectures, sampling methods, and diagnostic tools. In addition, it provides well-tested default settings but also offers flexibility to fully customize every step of the simulation-based inference workflow. Taken together, the $\texttt{sbi}$ toolkit enables scientists and engineers to apply state-of-the-art SBI methods to black-box simulators, opening up new possibilities for aligning simulations with empirically observed data.

Reduce, Reuse, Recycle: Compositional Generation with Energy-Based Diffusion Models and MCMC

Since their introduction, diffusion models have quickly become the prevailing approach to generative modeling in many domains. They can be interpreted as learning the gradients of a time-varying sequence of log-probability density functions. This interpretation has motivated classifier-based and classifier-free guidance as methods for post-hoc control of diffusion models. In this work, we build upon these ideas using the score-based interpretation of diffusion models, and explore alternative ways to condition, modify, and reuse diffusion models for tasks involving compositional generation and guidance. In particular, we investigate why certain types of composition fail using current techniques and present a number of solutions. We conclude that the sampler (not the model) is responsible for this failure and propose new samplers, inspired by MCMC, which enable successful compositional generation. Further, we propose an energy-based parameterization of diffusion models which enables the use of new compositional operators and more sophisticated, Metropolis-corrected samplers. Intriguingly we find these samplers lead to notable improvements in compositional generation across a wide set of problems such as classifier-guided ImageNet modeling and compositional text-to-image generation.

Continuous diffusion for categorical data

Diffusion models have quickly become the go-to paradigm for generative modelling of perceptual signals (such as images and sound) through iterative refinement. Their success hinges on the fact that the underlying physical phenomena are continuous. For inherently discrete and categorical data such as language, various diffusion-inspired alternatives have been proposed. However, the continuous nature of diffusion models conveys many benefits, and in this work we endeavour to preserve it. We propose CDCD, a framework for modelling categorical data with diffusion models that are continuous both in time and input space. We demonstrate its efficacy on several language modelling tasks.

On Maximum Likelihood Training of Score-Based Generative Models

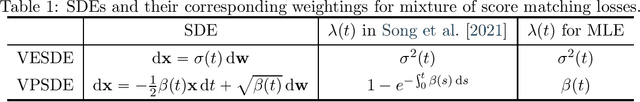
Score-based generative modeling has recently emerged as a promising alternative to traditional likelihood-based or implicit approaches. Learning in score-based models involves first perturbing data with a continuous-time stochastic process, and then matching the time-dependent gradient of the logarithm of the noisy data density - or score function - using a continuous mixture of score matching losses. In this note, we show that such an objective is equivalent to maximum likelihood for certain choices of mixture weighting. This connection provides a principled way to weight the objective function, and justifies its use for comparing different score-based generative models. Taken together with previous work, our result reveals that both maximum likelihood training and test-time log-likelihood evaluation can be achieved through parameterization of the score function alone, without the need to explicitly parameterize a density function.

SBI -- A toolkit for simulation-based inference

Scientists and engineers employ stochastic numerical simulators to model empirically observed phenomena. In contrast to purely statistical models, simulators express scientific principles that provide powerful inductive biases, improve generalization to new data or scenarios and allow for fewer, more interpretable and domain-relevant parameters. Despite these advantages, tuning a simulator's parameters so that its outputs match data is challenging. Simulation-based inference (SBI) seeks to identify parameter sets that a) are compatible with prior knowledge and b) match empirical observations. Importantly, SBI does not seek to recover a single 'best' data-compatible parameter set, but rather to identify all high probability regions of parameter space that explain observed data, and thereby to quantify parameter uncertainty. In Bayesian terminology, SBI aims to retrieve the posterior distribution over the parameters of interest. In contrast to conventional Bayesian inference, SBI is also applicable when one can run model simulations, but no formula or algorithm exists for evaluating the probability of data given parameters, i.e. the likelihood. We present $\texttt{sbi}$, a PyTorch-based package that implements SBI algorithms based on neural networks. $\texttt{sbi}$ facilitates inference on black-box simulators for practising scientists and engineers by providing a unified interface to state-of-the-art algorithms together with documentation and tutorials.

On Contrastive Learning for Likelihood-free Inference

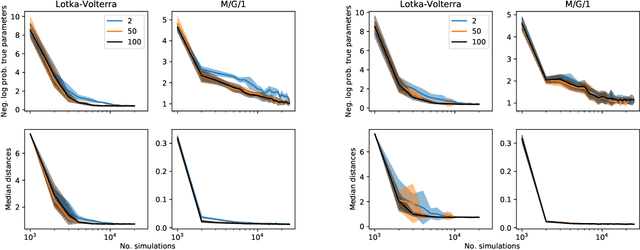
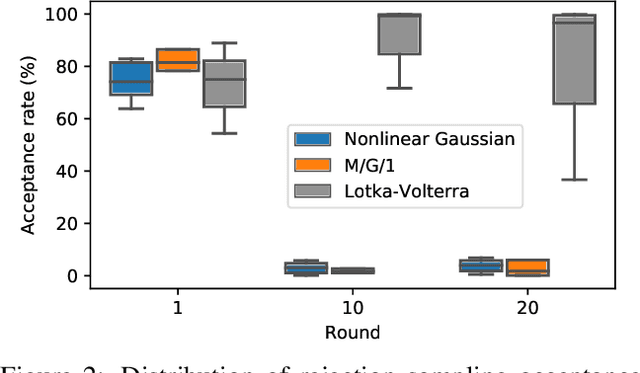
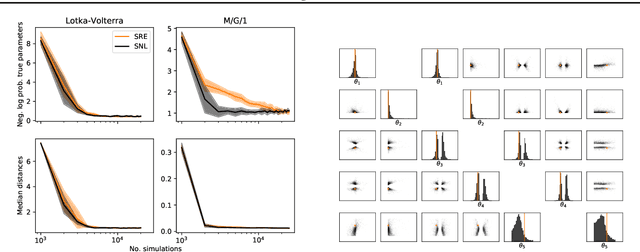
Likelihood-free methods perform parameter inference in stochastic simulator models where evaluating the likelihood is intractable but sampling synthetic data is possible. One class of methods for this likelihood-free problem uses a classifier to distinguish between pairs of parameter-observation samples generated using the simulator and pairs sampled from some reference distribution, which implicitly learns a density ratio proportional to the likelihood. Another popular class of methods fits a conditional distribution to the parameter posterior directly, and a particular recent variant allows for the use of flexible neural density estimators for this task. In this work, we show that both of these approaches can be unified under a general contrastive learning scheme, and clarify how they should be run and compared.

Neural Spline Flows

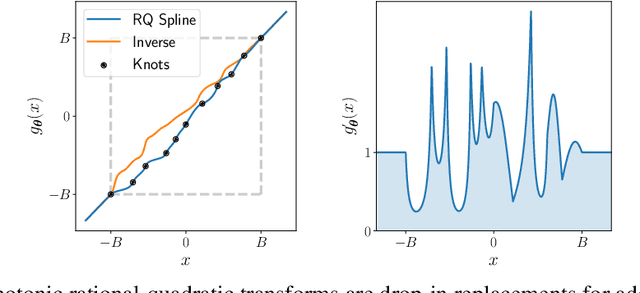
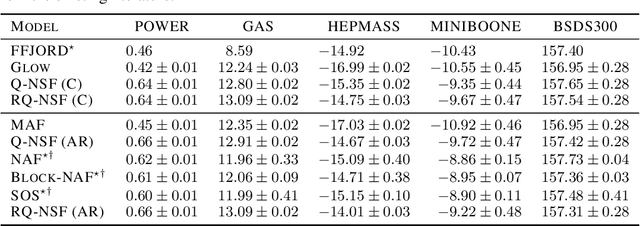
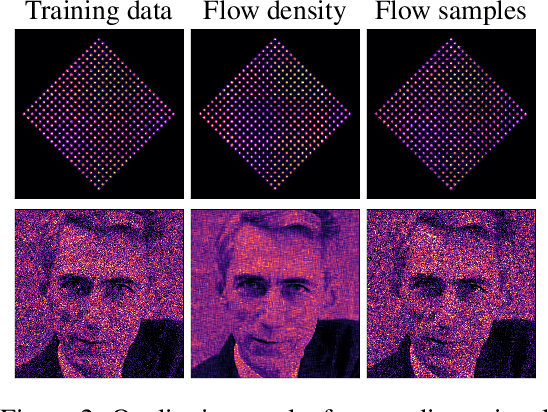
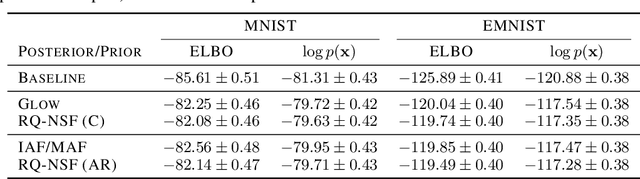
A normalizing flow models a complex probability density as an invertible transformation of a simple base density. Flows based on either coupling or autoregressive transforms both offer exact density evaluation and sampling, but rely on the parameterization of an easily invertible elementwise transformation, whose choice determines the flexibility of these models. Building upon recent work, we propose a fully-differentiable module based on monotonic rational-quadratic splines, which enhances the flexibility of both coupling and autoregressive transforms while retaining analytic invertibility. We demonstrate that neural spline flows improve density estimation, variational inference, and generative modeling of images.

Cubic-Spline Flows

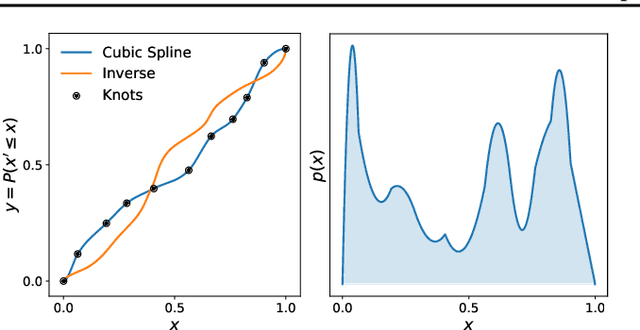
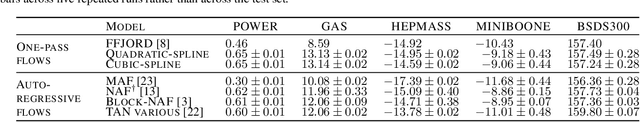
A normalizing flow models a complex probability density as an invertible transformation of a simple density. The invertibility means that we can evaluate densities and generate samples from a flow. In practice, autoregressive flow-based models are slow to invert, making either density estimation or sample generation slow. Flows based on coupling transforms are fast for both tasks, but have previously performed less well at density estimation than autoregressive flows. We stack a new coupling transform, based on monotonic cubic splines, with LU-decomposed linear layers. The resulting cubic-spline flow retains an exact one-pass inverse, can be used to generate high-quality images, and closes the gap with autoregressive flows on a suite of density-estimation tasks.

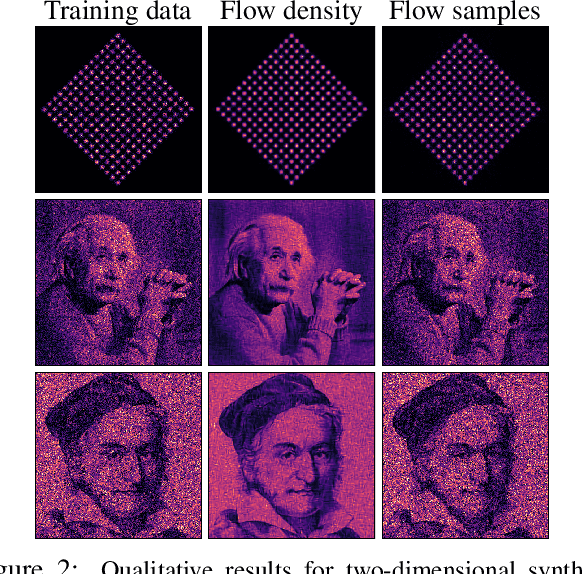
Autoregressive Energy Machines

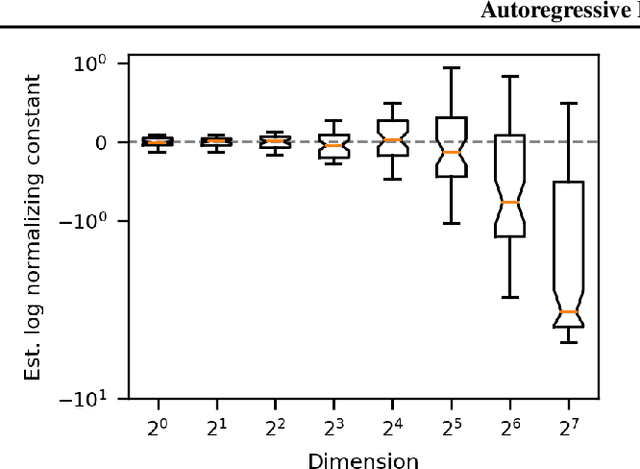
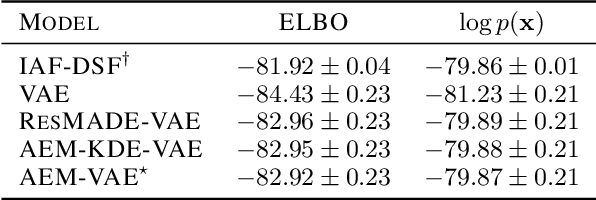
Neural density estimators are flexible families of parametric models which have seen widespread use in unsupervised machine learning in recent years. Maximum-likelihood training typically dictates that these models be constrained to specify an explicit density. However, this limitation can be overcome by instead using a neural network to specify an energy function, or unnormalized density, which can subsequently be normalized to obtain a valid distribution. The challenge with this approach lies in accurately estimating the normalizing constant of the high-dimensional energy function. We propose the Autoregressive Energy Machine, an energy-based model which simultaneously learns an unnormalized density and computes an importance-sampling estimate of the normalizing constant for each conditional in an autoregressive decomposition. The Autoregressive Energy Machine achieves state-of-the-art performance on a suite of density-estimation tasks.

Sequential Neural Methods for Likelihood-free Inference

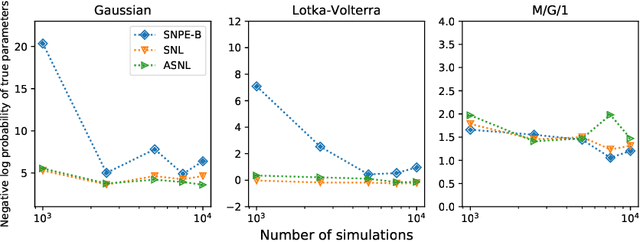
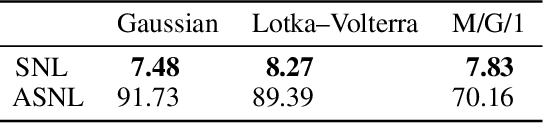
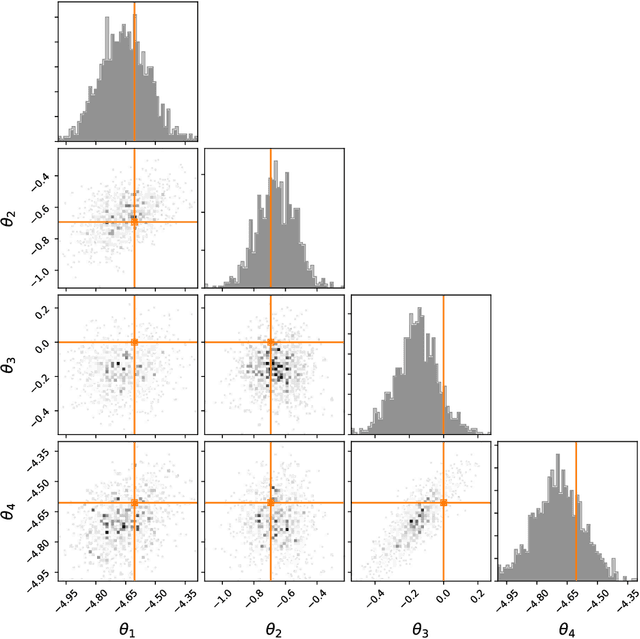
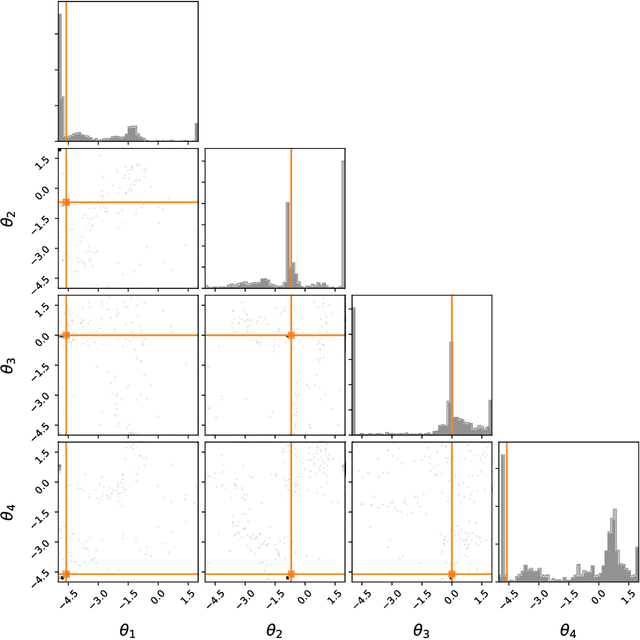
Likelihood-free inference refers to inference when a likelihood function cannot be explicitly evaluated, which is often the case for models based on simulators. Most of the literature is based on sample-based `Approximate Bayesian Computation' methods, but recent work suggests that approaches based on deep neural conditional density estimators can obtain state-of-the-art results with fewer simulations. The neural approaches vary in how they choose which simulations to run and what they learn: an approximate posterior or a surrogate likelihood. This work provides some direct controlled comparisons between these choices.