How Deep Are Deep GPs, Really? A Sharp Threshold and a Non-Gaussian Limit for Compositional GPs

Compositional priors describe the generic properties of layered functions in deep Bayesian models, where deep neural networks with random weights are a canonical example.In the wide-network limit, the prior is a Gaussian process with a depth-dependent kernel, and its behaviour as depth grows has been extensively studied through this kernel. Here, we study another case, where each layer itself is a vector valued Gaussian process, and our aim is similarly to understand the limiting behaviour of the prior as depth grows. Previous GP work has established that for the RBF kernel and a certain range of bandwidths $r$, the prior degenerates in the limit, converging to the set of constant functions -- which is not useful as a probabilistic model. In this paper we establish several new results. First, we identify a sharp bandwidth threshold $r_c(d) = Θ(\sqrt{d})$ above which the limit is degenerate, strengthening the earlier bounds. Second, and more importantly, we show that for $r$ below the threshold $r_c(d)$ the prior converges to a limit distribution $π_{\bar{Z}}$. We also prove that these distributions are non-degenerate and non-Gaussian, with non-vanishing dependence between coordinates. In contrast to the previously known degenerate regime, deep Gaussian process priors can therefore admit non-trivial limits. Empirically, we verify the threshold across a range of dimensions $d$, and demonstrate a complex multimodal behaviour of the limit distributions $π_{\bar{Z}}$ -- a regime that becomes increasingly narrow with $d$ and would be hard to identify without knowing the threshold.

The Value of Mechanistic Priors in Sequential Decision Making

Hybrid mechanistic models, physical priors with learned residuals, promise to reduce the data required for good decisions, but have no computable criterion to test this. We characterize the value of mechanistic priors in sequential decision-making within both asymptotic and burn-in regimes. To formalize this, we introduce the mechanistic information of a model -- the mutual information between the model's recommended policy $\hatπ$ and the true optimal policy $π^*$ -- quantified via an occupancy-weighted bias $B_μ$. In the asymptotic regime (large $N$), matched bounds reveal that Bayesian regret scales with the residual entropy $H_{\mathrm{mech}}$, delivering a theoretical sample complexity reduction of $H(μ)/H_{\mathrm{mech}}$ compared to an uninformed baseline. Furthermore, we provide a model certificate to determine empirical sample efficiency. Complementarily, in the clinically relevant burn-in regime (small $N$), we establish a lower bound on the penalty incurred by confidently wrong priors. We demonstrate both the asymptotic and burn-in bounds across 5-fluorouracil (5-FU) dosing simulations motivated by published FOLFOX pharmacokinetic data, where a hybrid prior yields large sample-efficiency gains in the burn-in regime. Finally, we contrast these grounded models with LLM priors, demonstrating that LLMs can suffer severe losses in mechanistic information, thereby motivating the exclusive use of physically-grounded priors for safety-critical applications.

Horizon Imagination: Efficient On-Policy Training in Diffusion World Models

We study diffusion-based world models for reinforcement learning, which offer high generative fidelity but face critical efficiency challenges in control. Current methods either require heavyweight models at inference or rely on highly sequential imagination, both of which impose prohibitive computational costs. We propose Horizon Imagination (HI), an on-policy imagination process for discrete stochastic policies that denoises multiple future observations in parallel. HI incorporates a stabilization mechanism and a novel sampling schedule that decouples the denoising budget from the effective horizon over which denoising is applied while also supporting sub-frame budgets. Experiments on Atari 100K and Craftium show that our approach maintains control performance with a sub-frame budget of half the denoising steps and achieves superior generation quality under varied schedules. Code is available at https://github.com/leor-c/horizon-imagination.

Optimal Sample Complexity for Single Time-Scale Actor-Critic with Momentum

We establish an optimal sample complexity of $O(ε^{-2})$ for obtaining an $ε$-optimal global policy using a single-timescale actor-critic (AC) algorithm in infinite-horizon discounted Markov decision processes (MDPs) with finite state-action spaces, improving upon the prior state of the art of $O(ε^{-3})$. Our approach applies STORM (STOchastic Recursive Momentum) to reduce variance in the critic updates. However, because samples are drawn from a nonstationary occupancy measure induced by the evolving policy, variance reduction via STORM alone is insufficient. To address this challenge, we maintain a buffer of small fraction of recent samples and uniformly sample from it for each critic update. Importantly, these mechanisms are compatible with existing deep learning architectures and require only minor modifications, without compromising practical applicability.

VLM-Guided Experience Replay

Recent advances in Large Language Models (LLMs) and Vision-Language Models (VLMs) have enabled powerful semantic and multimodal reasoning capabilities, creating new opportunities to enhance sample efficiency, high-level planning, and interpretability in reinforcement learning (RL). While prior work has integrated LLMs and VLMs into various components of RL, the replay buffer, a core component for storing and reusing experiences, remains unexplored. We propose addressing this gap by leveraging VLMs to guide the prioritization of experiences in the replay buffer. Our key idea is to use a frozen, pre-trained VLM (requiring no fine-tuning) as an automated evaluator to identify and prioritize promising sub-trajectories from the agent's experiences. Across scenarios, including game-playing and robotics, spanning both discrete and continuous domains, agents trained with our proposed prioritization method achieve 11-52% higher average success rates and improve sample efficiency by 19-45% compared to previous approaches. https://esharony.me/projects/vlm-rb/

Spectral Bellman Method: Unifying Representation and Exploration in RL

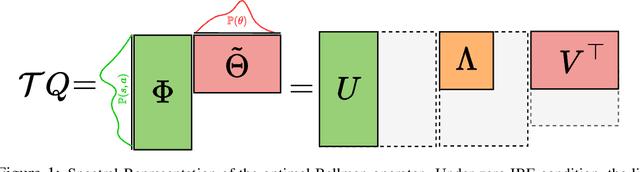
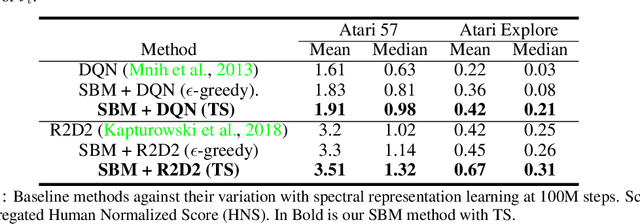
The effect of representation has been demonstrated in reinforcement learning, from both theoretical and empirical successes. However, the existing representation learning mainly induced from model learning aspects, misaligning with our RL tasks. This work introduces Spectral Bellman Representation, a novel framework derived from the Inherent Bellman Error (IBE) condition, which aligns with the fundamental structure of Bellman updates across a space of possible value functions, therefore, directly towards value-based RL. Our key insight is the discovery of a fundamental spectral relationship: under the zero-IBE condition, the transformation of a distribution of value functions by the Bellman operator is intrinsically linked to the feature covariance structure. This spectral connection yields a new, theoretically-grounded objective for learning state-action features that inherently capture this Bellman-aligned covariance. Our method requires a simple modification to existing algorithms. We demonstrate that our learned representations enable structured exploration, by aligning feature covariance with Bellman dynamics, and improve overall performance, particularly in challenging hard-exploration and long-horizon credit assignment tasks. Our framework naturally extends to powerful multi-step Bellman operators, further broadening its impact. Spectral Bellman Representation offers a principled and effective path toward learning more powerful and structurally sound representations for value-based reinforcement learning.

State Entropy Regularization for Robust Reinforcement Learning

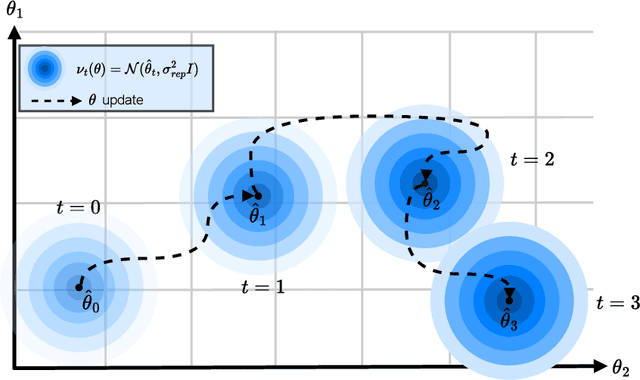
State entropy regularization has empirically shown better exploration and sample complexity in reinforcement learning (RL). However, its theoretical guarantees have not been studied. In this paper, we show that state entropy regularization improves robustness to structured and spatially correlated perturbations. These types of variation are common in transfer learning but often overlooked by standard robust RL methods, which typically focus on small, uncorrelated changes. We provide a comprehensive characterization of these robustness properties, including formal guarantees under reward and transition uncertainty, as well as settings where the method performs poorly. Much of our analysis contrasts state entropy with the widely used policy entropy regularization, highlighting their different benefits. Finally, from a practical standpoint, we illustrate that compared with policy entropy, the robustness advantages of state entropy are more sensitive to the number of rollouts used for policy evaluation.

Policy Gradient with Tree Search: Avoiding Local Optimas through Lookahead

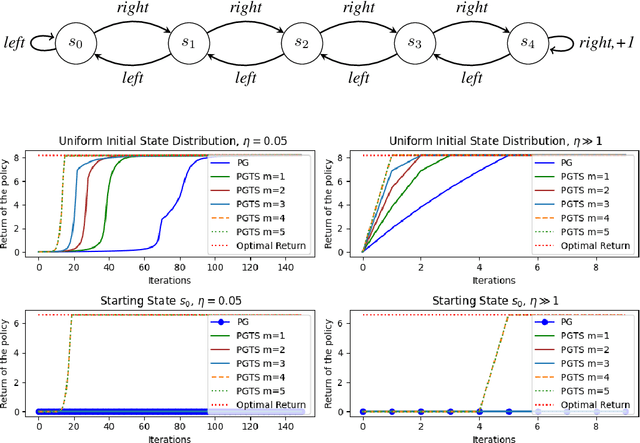
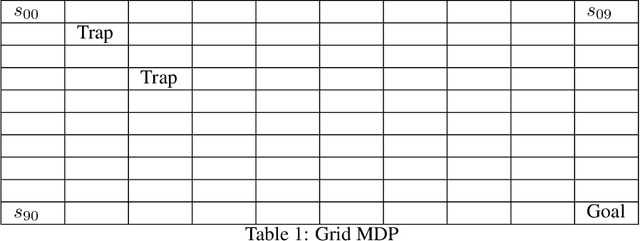
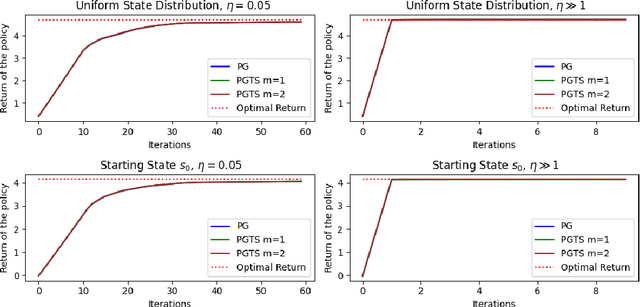
Classical policy gradient (PG) methods in reinforcement learning frequently converge to suboptimal local optima, a challenge exacerbated in large or complex environments. This work investigates Policy Gradient with Tree Search (PGTS), an approach that integrates an $m$-step lookahead mechanism to enhance policy optimization. We provide theoretical analysis demonstrating that increasing the tree search depth $m$-monotonically reduces the set of undesirable stationary points and, consequently, improves the worst-case performance of any resulting stationary policy. Critically, our analysis accommodates practical scenarios where policy updates are restricted to states visited by the current policy, rather than requiring updates across the entire state space. Empirical evaluations on diverse MDP structures, including Ladder, Tightrope, and Gridworld environments, illustrate PGTS's ability to exhibit "farsightedness," navigate challenging reward landscapes, escape local traps where standard PG fails, and achieve superior solutions.

Policy Optimized Text-to-Image Pipeline Design

Text-to-image generation has evolved beyond single monolithic models to complex multi-component pipelines. These combine fine-tuned generators, adapters, upscaling blocks and even editing steps, leading to significant improvements in image quality. However, their effective design requires substantial expertise. Recent approaches have shown promise in automating this process through large language models (LLMs), but they suffer from two critical limitations: extensive computational requirements from generating images with hundreds of predefined pipelines, and poor generalization beyond memorized training examples. We introduce a novel reinforcement learning-based framework that addresses these inefficiencies. Our approach first trains an ensemble of reward models capable of predicting image quality scores directly from prompt-workflow combinations, eliminating the need for costly image generation during training. We then implement a two-phase training strategy: initial workflow vocabulary training followed by GRPO-based optimization that guides the model toward higher-performing regions of the workflow space. Additionally, we incorporate a classifier-free guidance based enhancement technique that extrapolates along the path between the initial and GRPO-tuned models, further improving output quality. We validate our approach through a set of comparisons, showing that it can successfully create new flows with greater diversity and lead to superior image quality compared to existing baselines.

Adversarial Bandit over Bandits: Hierarchical Bandits for Online Configuration Management

Motivated by dynamic parameter optimization in finite, but large action (configurations) spaces, this work studies the nonstochastic multi-armed bandit (MAB) problem in metric action spaces with oblivious Lipschitz adversaries. We propose ABoB, a hierarchical Adversarial Bandit over Bandits algorithm that can use state-of-the-art existing "flat" algorithms, but additionally clusters similar configurations to exploit local structures and adapt to changing environments. We prove that in the worst-case scenario, such clustering approach cannot hurt too much and ABoB guarantees a standard worst-case regret bound of $O\left(k^{\frac{1}{2}}T^{\frac{1}{2}}\right)$, where $T$ is the number of rounds and $k$ is the number of arms, matching the traditional flat approach. However, under favorable conditions related to the algorithm properties, clusters properties, and certain Lipschitz conditions, the regret bound can be improved to $O\left(k^{\frac{1}{4}}T^{\frac{1}{2}}\right)$. Simulations and experiments on a real storage system demonstrate that ABoB, using standard algorithms like EXP3 and Tsallis-INF, achieves lower regret and faster convergence than the flat method, up to 50% improvement in known previous setups, nonstochastic and stochastic, as well as in our settings.