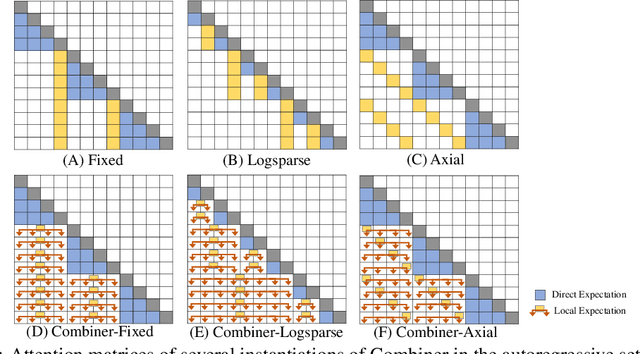
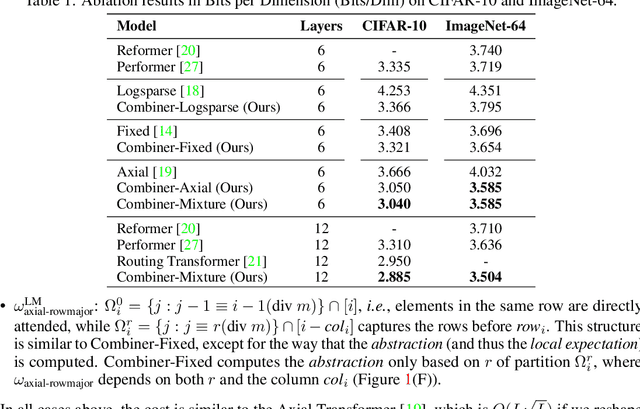
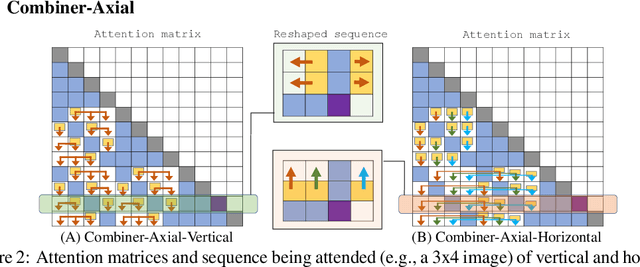
Combiner: Full Attention Transformer with Sparse Computation Cost

Transformers provide a class of expressive architectures that are extremely effective for sequence modeling. However, the key limitation of transformers is their quadratic memory and time complexity $\mathcal{O}(L^2)$ with respect to the sequence length in attention layers, which restricts application in extremely long sequences. Most existing approaches leverage sparsity or low-rank assumptions in the attention matrix to reduce cost, but sacrifice expressiveness. Instead, we propose Combiner, which provides full attention capability in each attention head while maintaining low computation and memory complexity. The key idea is to treat the self-attention mechanism as a conditional expectation over embeddings at each location, and approximate the conditional distribution with a structured factorization. Each location can attend to all other locations, either via direct attention, or through indirect attention to abstractions, which are again conditional expectations of embeddings from corresponding local regions. We show that most sparse attention patterns used in existing sparse transformers are able to inspire the design of such factorization for full attention, resulting in the same sub-quadratic cost ($\mathcal{O}(L\log(L))$ or $\mathcal{O}(L\sqrt{L})$). Combiner is a drop-in replacement for attention layers in existing transformers and can be easily implemented in common frameworks. An experimental evaluation on both autoregressive and bidirectional sequence tasks demonstrates the effectiveness of this approach, yielding state-of-the-art results on several image and text modeling tasks.

SpreadsheetCoder: Formula Prediction from Semi-structured Context

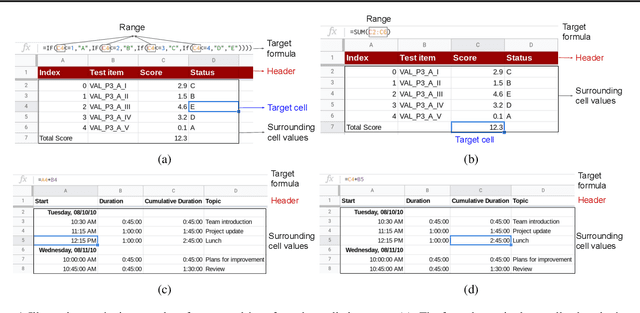
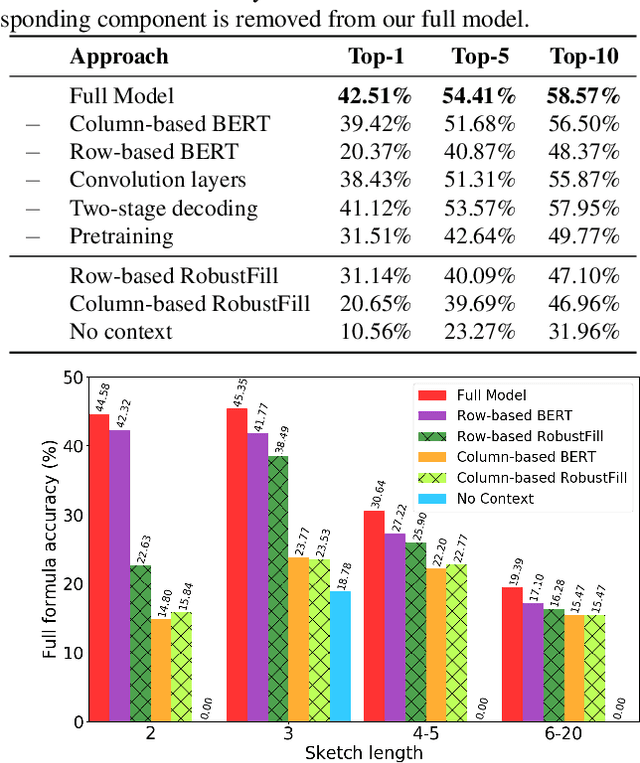
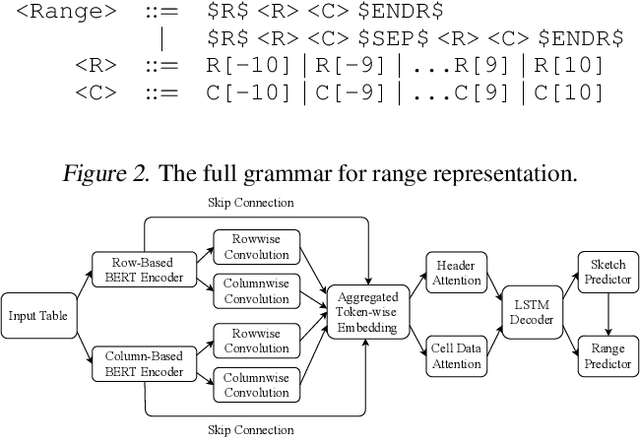
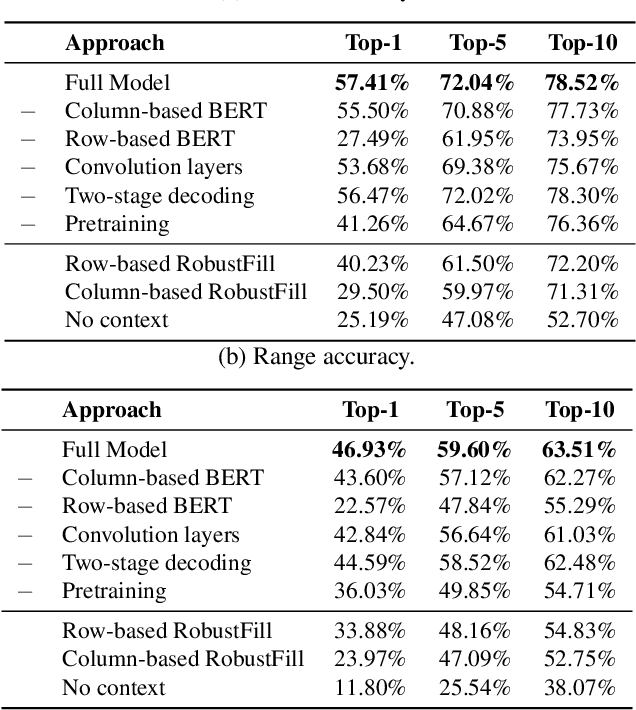
Spreadsheet formula prediction has been an important program synthesis problem with many real-world applications. Previous works typically utilize input-output examples as the specification for spreadsheet formula synthesis, where each input-output pair simulates a separate row in the spreadsheet. However, this formulation does not fully capture the rich context in real-world spreadsheets. First, spreadsheet data entries are organized as tables, thus rows and columns are not necessarily independent from each other. In addition, many spreadsheet tables include headers, which provide high-level descriptions of the cell data. However, previous synthesis approaches do not consider headers as part of the specification. In this work, we present the first approach for synthesizing spreadsheet formulas from tabular context, which includes both headers and semi-structured tabular data. In particular, we propose SpreadsheetCoder, a BERT-based model architecture to represent the tabular context in both row-based and column-based formats. We train our model on a large dataset of spreadsheets, and demonstrate that SpreadsheetCoder achieves top-1 prediction accuracy of 42.51%, which is a considerable improvement over baselines that do not employ rich tabular context. Compared to the rule-based system, SpreadsheetCoder assists 82% more users in composing formulas on Google Sheets.

Learning Discrete Energy-based Models via Auxiliary-variable Local Exploration

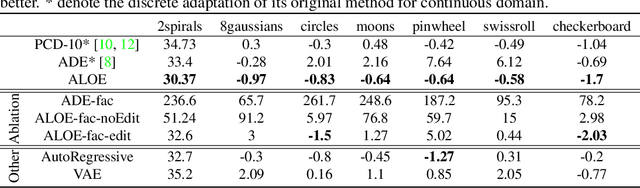
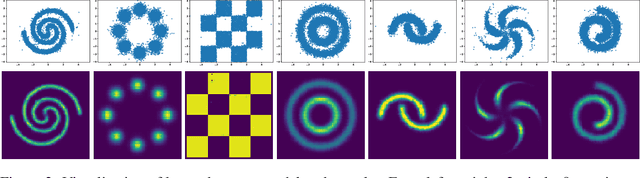
Discrete structures play an important role in applications like program language modeling and software engineering. Current approaches to predicting complex structures typically consider autoregressive models for their tractability, with some sacrifice in flexibility. Energy-based models (EBMs) on the other hand offer a more flexible and thus more powerful approach to modeling such distributions, but require partition function estimation. In this paper we propose ALOE, a new algorithm for learning conditional and unconditional EBMs for discrete structured data, where parameter gradients are estimated using a learned sampler that mimics local search. We show that the energy function and sampler can be trained efficiently via a new variational form of power iteration, achieving a better trade-off between flexibility and tractability. Experimentally, we show that learning local search leads to significant improvements in challenging application domains. Most notably, we present an energy model guided fuzzer for software testing that achieves comparable performance to well engineered fuzzing engines like libfuzzer.

Polymers for Extreme Conditions Designed Using Syntax-Directed Variational Autoencoders

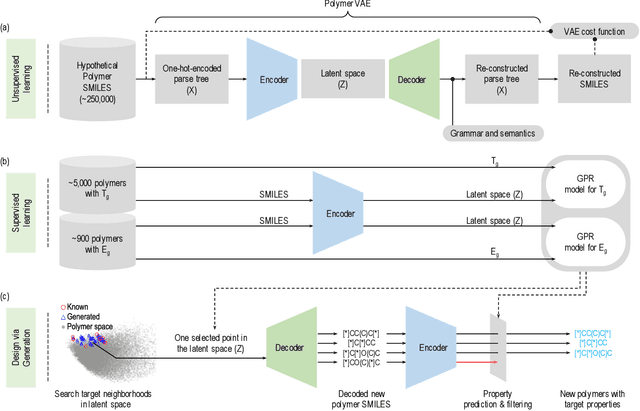
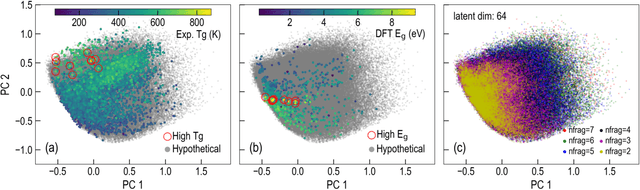
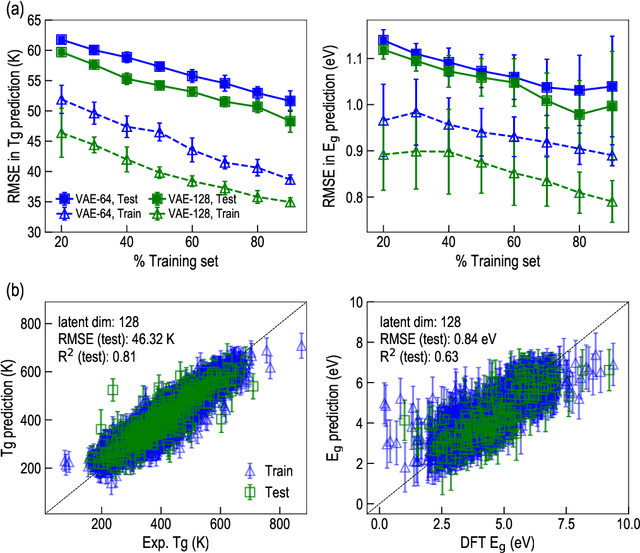
The design/discovery of new materials is highly non-trivial owing to the near-infinite possibilities of material candidates, and multiple required property/performance objectives. Thus, machine learning tools are now commonly employed to virtually screen material candidates with desired properties by learning a theoretical mapping from material-to-property space, referred to as the \emph{forward} problem. However, this approach is inefficient, and severely constrained by the candidates that human imagination can conceive. Thus, in this work on polymers, we tackle the materials discovery challenge by solving the \emph{inverse} problem: directly generating candidates that satisfy desired property/performance objectives. We utilize syntax-directed variational autoencoders (VAE) in tandem with Gaussian process regression (GPR) models to discover polymers expected to be robust under three extreme conditions: (1) high temperatures, (2) high electric field, and (3) high temperature \emph{and} high electric field, useful for critical structural, electrical and energy storage applications. This approach to learn from (and augment) human ingenuity is general, and can be extended to discover polymers with other targeted properties and performance measures.

Energy-based View of Retrosynthesis

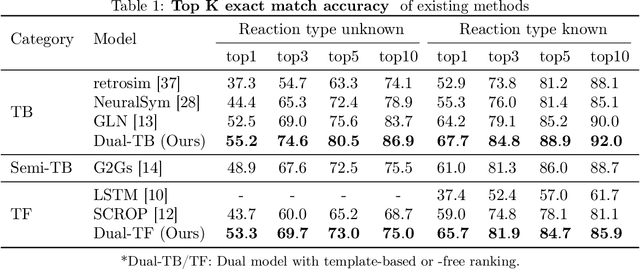
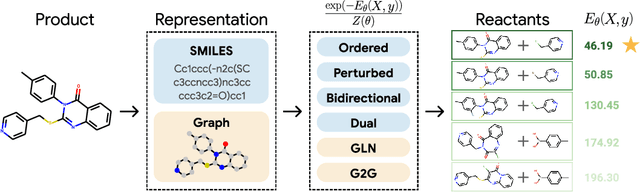
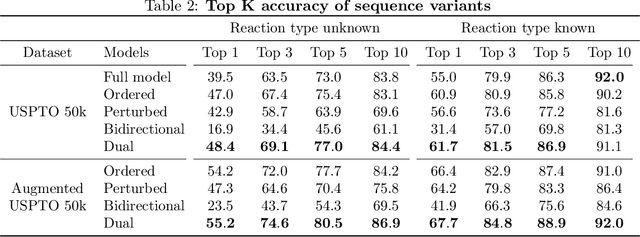
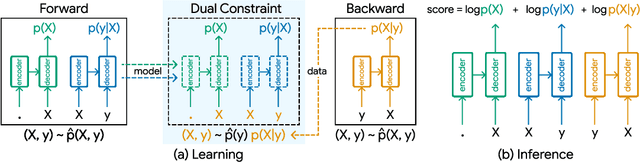
Retrosynthesis -- the process of identifying a set of reactants to synthesize a target molecule -- is of vital importance to material design and drug discovery. Existing machine learning approaches based on language models and graph neural networks have achieved encouraging results. In this paper, we propose a framework that unifies sequence- and graph-based methods as energy-based models (EBMs) with different energy functions. This unified perspective provides critical insights about EBM variants through a comprehensive assessment of performance. Additionally, we present a novel dual variant within the framework that performs consistent training over Bayesian forward- and backward-prediction by constraining the agreement between the two directions. This model improves state-of-the-art performance by 9.6% for template-free approaches where the reaction type is unknown.

Retro*: Learning Retrosynthetic Planning with Neural Guided A* Search

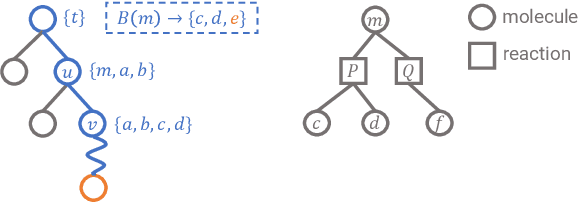
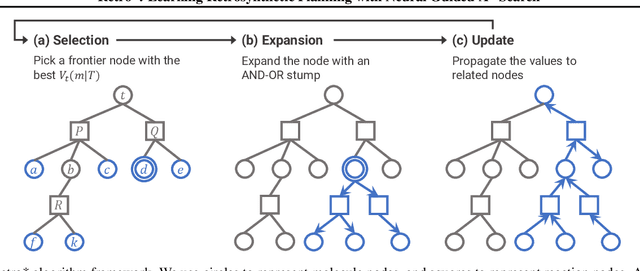
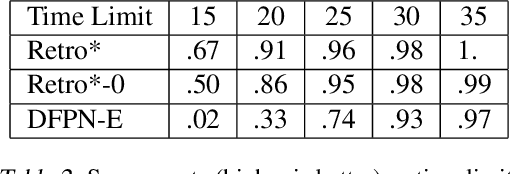
Retrosynthetic planning is a critical task in organic chemistry which identifies a series of reactions that can lead to the synthesis of a target product. The vast number of possible chemical transformations makes the size of the search space very big, and retrosynthetic planning is challenging even for experienced chemists. However, existing methods either require expensive return estimation by rollout with high variance, or optimize for search speed rather than the quality. In this paper, we propose Retro*, a neural-based A*-like algorithm that finds high-quality synthetic routes efficiently. It maintains the search as an AND-OR tree, and learns a neural search bias with off-policy data. Then guided by this neural network, it performs best-first search efficiently during new planning episodes. Experiments on benchmark USPTO datasets show that, our proposed method outperforms existing state-of-the-art with respect to both the success rate and solution quality, while being more efficient at the same time.

Scalable Deep Generative Modeling for Sparse Graphs

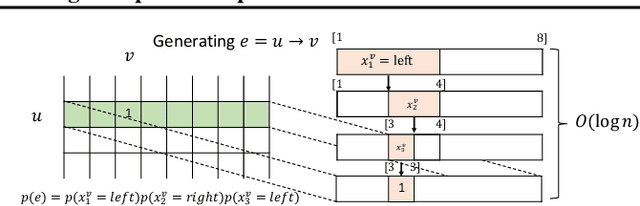
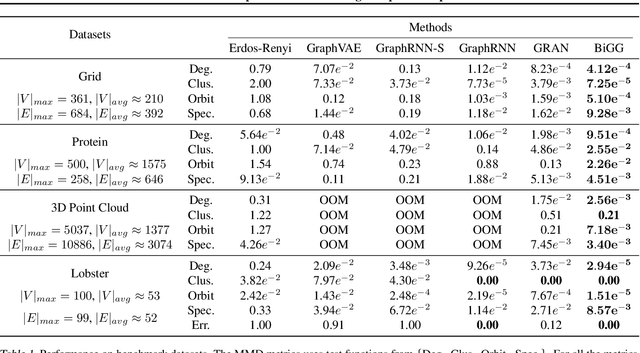
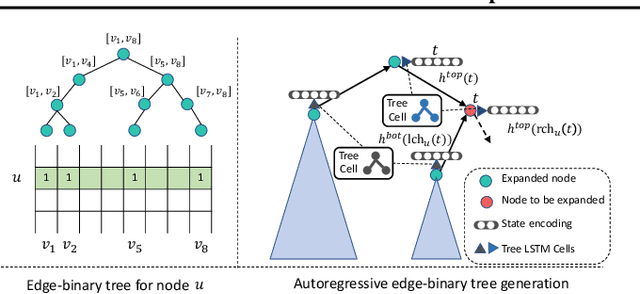
Learning graph generative models is a challenging task for deep learning and has wide applicability to a range of domains like chemistry, biology and social science. However current deep neural methods suffer from limited scalability: for a graph with $n$ nodes and $m$ edges, existing deep neural methods require $\Omega(n^2)$ complexity by building up the adjacency matrix. On the other hand, many real world graphs are actually sparse in the sense that $m\ll n^2$. Based on this, we develop a novel autoregressive model, named BiGG, that utilizes this sparsity to avoid generating the full adjacency matrix, and importantly reduces the graph generation time complexity to $O((n + m)\log n)$. Furthermore, during training this autoregressive model can be parallelized with $O(\log n)$ synchronization stages, which makes it much more efficient than other autoregressive models that require $\Omega(n)$. Experiments on several benchmarks show that the proposed approach not only scales to orders of magnitude larger graphs than previously possible with deep autoregressive graph generative models, but also yields better graph generation quality.

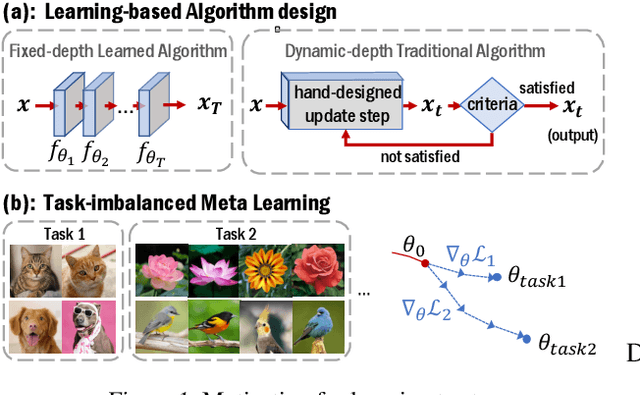
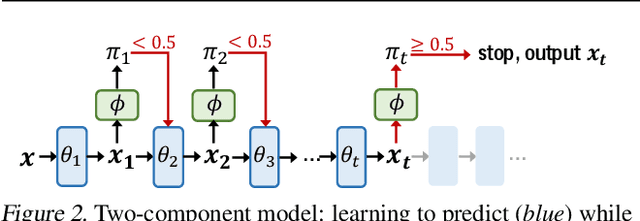
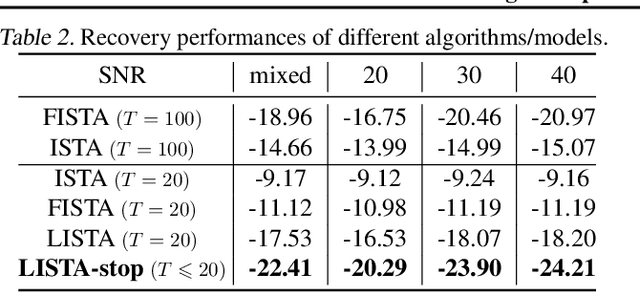
Learning to Stop While Learning to Predict

There is a recent surge of interest in designing deep architectures based on the update steps in traditional algorithms, or learning neural networks to improve and replace traditional algorithms. While traditional algorithms have certain stopping criteria for outputting results at different iterations, many algorithm-inspired deep models are restricted to a ``fixed-depth'' for all inputs. Similar to algorithms, the optimal depth of a deep architecture may be different for different input instances, either to avoid ``over-thinking'', or because we want to compute less for operations converged already. In this paper, we tackle this varying depth problem using a steerable architecture, where a feed-forward deep model and a variational stopping policy are learned together to sequentially determine the optimal number of layers for each input instance. Training such architecture is very challenging. We provide a variational Bayes perspective and design a novel and effective training procedure which decomposes the task into an oracle model learning stage and an imitation stage. Experimentally, we show that the learned deep model along with the stopping policy improves the performances on a diverse set of tasks, including learning sparse recovery, few-shot meta learning, and computer vision tasks.

Energy-Based Processes for Exchangeable Data

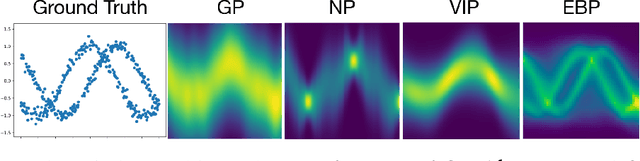
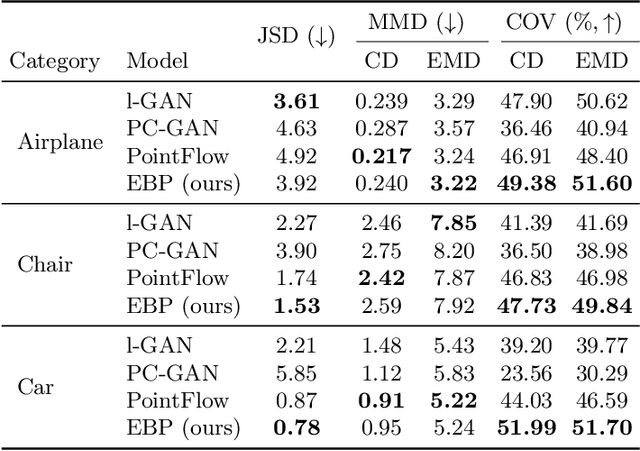
Recently there has been growing interest in modeling sets with exchangeability such as point clouds. A shortcoming of current approaches is that they restrict the cardinality of the sets considered or can only express limited forms of distribution over unobserved data. To overcome these limitations, we introduce Energy-Based Processes (EBPs), which extend energy based models to exchangeable data while allowing neural network parameterizations of the energy function. A key advantage of these models is the ability to express more flexible distributions over sets without restricting their cardinality. We develop an efficient training procedure for EBPs that demonstrates state-of-the-art performance on a variety of tasks such as point cloud generation, classification, denoising, and image completion.

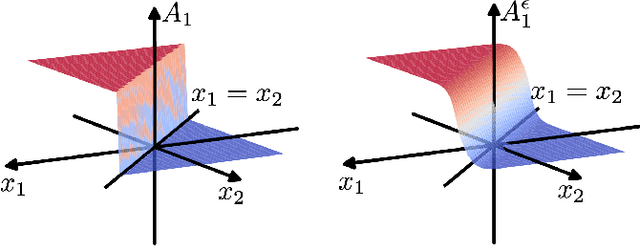
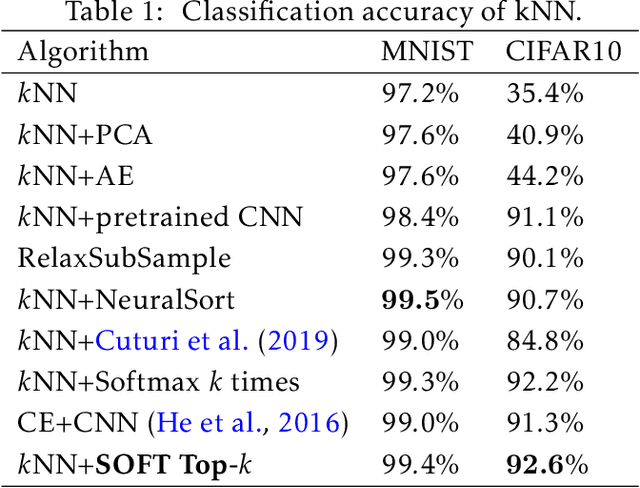
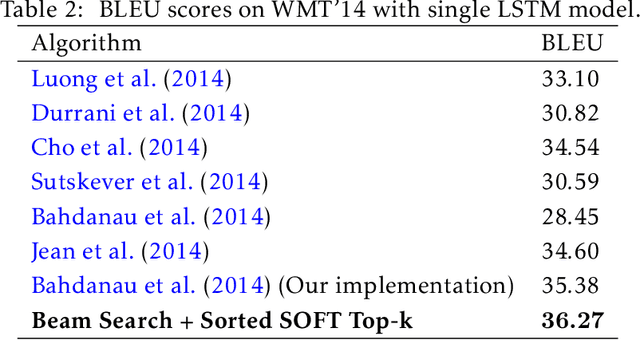
Differentiable Top-k Operator with Optimal Transport

The top-k operation, i.e., finding the k largest or smallest elements from a collection of scores, is an important model component, which is widely used in information retrieval, machine learning, and data mining. However, if the top-k operation is implemented in an algorithmic way, e.g., using bubble algorithm, the resulting model cannot be trained in an end-to-end way using prevalent gradient descent algorithms. This is because these implementations typically involve swapping indices, whose gradient cannot be computed. Moreover, the corresponding mapping from the input scores to the indicator vector of whether this element belongs to the top-k set is essentially discontinuous. To address the issue, we propose a smoothed approximation, namely the SOFT (Scalable Optimal transport-based diFferenTiable) top-k operator. Specifically, our SOFT top-k operator approximates the output of the top-k operation as the solution of an Entropic Optimal Transport (EOT) problem. The gradient of the SOFT operator can then be efficiently approximated based on the optimality conditions of EOT problem. We apply the proposed operator to the k-nearest neighbors and beam search algorithms, and demonstrate improved performance.