Exploiting Contextual Structure to Generate Useful Auxiliary Tasks

Reinforcement learning requires interaction with an environment, which is expensive for robots. This constraint necessitates approaches that work with limited environmental interaction by maximizing the reuse of previous experiences. We propose an approach that maximizes experience reuse while learning to solve a given task by generating and simultaneously learning useful auxiliary tasks. To generate these tasks, we construct an abstract temporal logic representation of the given task and leverage large language models to generate context-aware object embeddings that facilitate object replacements. Counterfactual reasoning and off-policy methods allow us to simultaneously learn these auxiliary tasks while solving the given target task. We combine these insights into a novel framework for multitask reinforcement learning and experimentally show that our generated auxiliary tasks share similar underlying exploration requirements as the given task, thereby maximizing the utility of directed exploration. Our approach allows agents to automatically learn additional useful policies without extra environment interaction.

A Domain-Agnostic Approach for Characterization of Lifelong Learning Systems

Despite the advancement of machine learning techniques in recent years, state-of-the-art systems lack robustness to "real world" events, where the input distributions and tasks encountered by the deployed systems will not be limited to the original training context, and systems will instead need to adapt to novel distributions and tasks while deployed. This critical gap may be addressed through the development of "Lifelong Learning" systems that are capable of 1) Continuous Learning, 2) Transfer and Adaptation, and 3) Scalability. Unfortunately, efforts to improve these capabilities are typically treated as distinct areas of research that are assessed independently, without regard to the impact of each separate capability on other aspects of the system. We instead propose a holistic approach, using a suite of metrics and an evaluation framework to assess Lifelong Learning in a principled way that is agnostic to specific domains or system techniques. Through five case studies, we show that this suite of metrics can inform the development of varied and complex Lifelong Learning systems. We highlight how the proposed suite of metrics quantifies performance trade-offs present during Lifelong Learning system development - both the widely discussed Stability-Plasticity dilemma and the newly proposed relationship between Sample Efficient and Robust Learning. Further, we make recommendations for the formulation and use of metrics to guide the continuing development of Lifelong Learning systems and assess their progress in the future.

On the Geometry of Reinforcement Learning in Continuous State and Action Spaces

Advances in reinforcement learning have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens. Central to our work is the idea that the transition dynamics induce a low dimensional manifold of reachable states embedded in the high-dimensional nominal state space. We prove that, under certain conditions, the dimensionality of this manifold is at most the dimensionality of the action space plus one. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments. We further demonstrate the applicability of our result by learning a policy in this low dimensional representation. To do so we introduce an algorithm that learns a mapping to a low dimensional representation, as a narrow hidden layer of a deep neural network, in tandem with the policy using DDPG. Our experiments show that a policy learnt this way perform on par or better for four MuJoCo control suite tasks.

Effects of Data Geometry in Early Deep Learning

Deep neural networks can approximate functions on different types of data, from images to graphs, with varied underlying structure. This underlying structure can be viewed as the geometry of the data manifold. By extending recent advances in the theoretical understanding of neural networks, we study how a randomly initialized neural network with piece-wise linear activation splits the data manifold into regions where the neural network behaves as a linear function. We derive bounds on the density of boundary of linear regions and the distance to these boundaries on the data manifold. This leads to insights into the expressivity of randomly initialized deep neural networks on non-Euclidean data sets. We empirically corroborate our theoretical results using a toy supervised learning problem. Our experiments demonstrate that number of linear regions varies across manifolds and the results hold with changing neural network architectures. We further demonstrate how the complexity of linear regions is different on the low dimensional manifold of images as compared to the Euclidean space, using the MetFaces dataset.

Evaluation Beyond Task Performance: Analyzing Concepts in AlphaZero in Hex

AlphaZero, an approach to reinforcement learning that couples neural networks and Monte Carlo tree search (MCTS), has produced state-of-the-art strategies for traditional board games like chess, Go, shogi, and Hex. While researchers and game commentators have suggested that AlphaZero uses concepts that humans consider important, it is unclear how these concepts are captured in the network. We investigate AlphaZero's internal representations in the game of Hex using two evaluation techniques from natural language processing (NLP): model probing and behavioral tests. In doing so, we introduce new evaluation tools to the RL community and illustrate how evaluations other than task performance can be used to provide a more complete picture of a model's strengths and weaknesses. Our analyses in the game of Hex reveal interesting patterns and generate some testable hypotheses about how such models learn in general. For example, we find that MCTS discovers concepts before the neural network learns to encode them. We also find that concepts related to short-term end-game planning are best encoded in the final layers of the model, whereas concepts related to long-term planning are encoded in the middle layers of the model.

Constrained Dynamic Movement Primitives for Safe Learning of Motor Skills

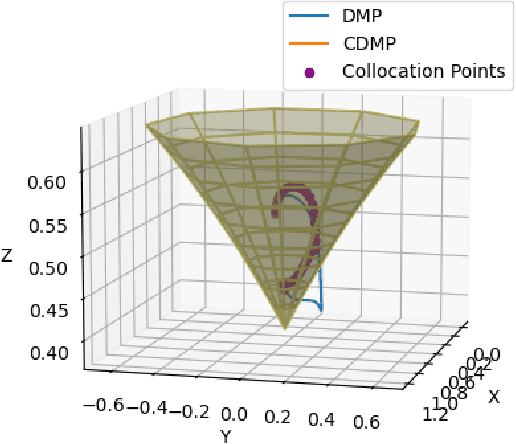
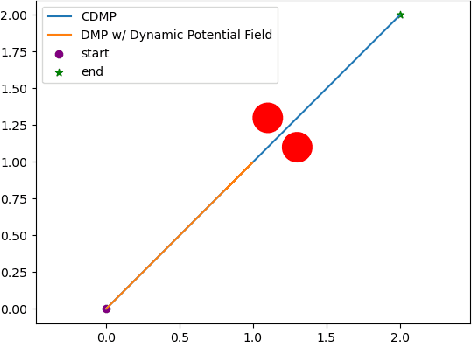
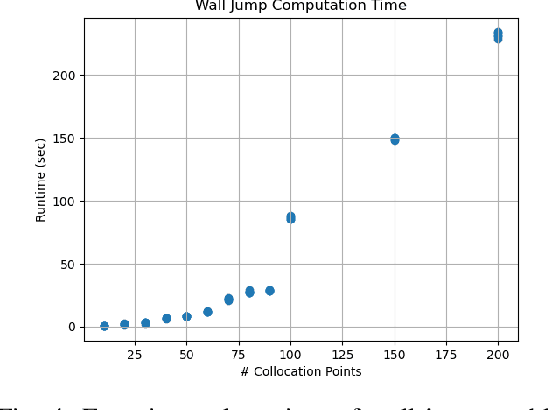
Dynamic movement primitives are widely used for learning skills which can be demonstrated to a robot by a skilled human or controller. While their generalization capabilities and simple formulation make them very appealing to use, they possess no strong guarantees to satisfy operational safety constraints for a task. In this paper, we present constrained dynamic movement primitives (CDMP) which can allow for constraint satisfaction in the robot workspace. We present a formulation of a non-linear optimization to perturb the DMP forcing weights regressed by locally-weighted regression to admit a Zeroing Barrier Function (ZBF), which certifies workspace constraint satisfaction. We demonstrate the proposed CDMP under different constraints on the end-effector movement such as obstacle avoidance and workspace constraints on a physical robot. A video showing the implementation of the proposed algorithm using different manipulators in different environments could be found here https://youtu.be/hJegJJkJfys.

RLang: A Declarative Language for Expression Prior Knowledge for Reinforcement Learning

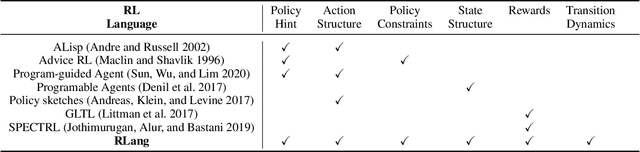
Communicating useful background knowledge to reinforcement learning (RL) agents is an important and effective method for accelerating learning. We introduce RLang, a domain-specific language (DSL) for communicating domain knowledge to an RL agent. Unlike other existing DSLs proposed by the RL community that ground to single elements of a decision-making formalism (e.g., the reward function or policy function), RLang can specify information about every element of a Markov decision process. We define precise syntax and grounding semantics for RLang, and provide a parser implementation that grounds RLang programs to an algorithm-agnostic partial world model and policy that can be exploited by an RL agent. We provide a series of example RLang programs, and demonstrate how different RL methods can exploit the resulting knowledge, including model-free and model-based tabular algorithms, hierarchical approaches, and deep RL algorithms (including both policy gradient and value-based methods).

Skill Transfer for Temporally-Extended Task Specifications

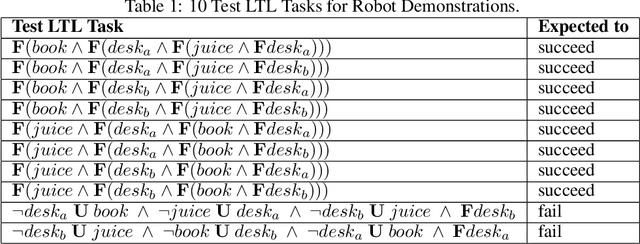
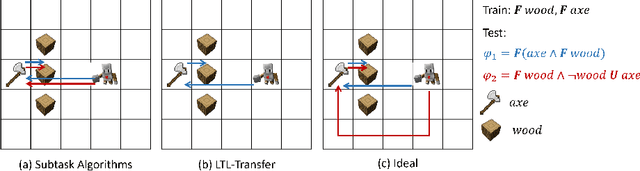
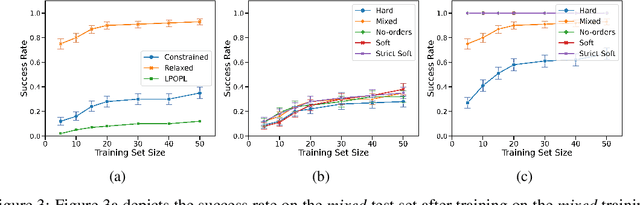
Deploying robots in real-world domains, such as households and flexible manufacturing lines, requires the robots to be taskable on demand. Linear temporal logic (LTL) is a widely-used specification language with a compositional grammar that naturally induces commonalities across tasks. However, the majority of prior research on reinforcement learning with LTL specifications treats every new formula independently. We propose LTL-Transfer, a novel algorithm that enables subpolicy reuse across tasks by segmenting policies for training tasks into portable transition-centric skills capable of satisfying a wide array of unseen LTL specifications while respecting safety-critical constraints. Our experiments in a Minecraft-inspired domain demonstrate the capability of LTL-Transfer to satisfy over 90% of 500 unseen tasks while training on only 50 task specifications and never violating a safety constraint. We also deployed LTL-Transfer on a quadruped mobile manipulator in a household environment to show its ability to transfer to many fetch and delivery tasks in a zero-shot fashion.

Meta-Learning Transferable Parameterized Skills

We propose a novel parameterized skill-learning algorithm that aims to learn transferable parameterized skills and synthesize them into a new action space that supports efficient learning in long-horizon tasks. We first propose novel learning objectives -- trajectory-centric diversity and smoothness -- that allow an agent to meta-learn reusable parameterized skills. Our agent can use these learned skills to construct a temporally-extended parameterized-action Markov decision process, for which we propose a hierarchical actor-critic algorithm that aims to efficiently learn a high-level control policy with the learned skills. We empirically demonstrate that the proposed algorithms enable an agent to solve a complicated long-horizon obstacle-course environment.

Characterizing the Action-Generalization Gap in Deep Q-Learning

We study the action generalization ability of deep Q-learning in discrete action spaces. Generalization is crucial for efficient reinforcement learning (RL) because it allows agents to use knowledge learned from past experiences on new tasks. But while function approximation provides deep RL agents with a natural way to generalize over state inputs, the same generalization mechanism does not apply to discrete action outputs. And yet, surprisingly, our experiments indicate that Deep Q-Networks (DQN), which use exactly this type of function approximator, are still able to achieve modest action generalization. Our main contribution is twofold: first, we propose a method of evaluating action generalization using expert knowledge of action similarity, and empirically confirm that action generalization leads to faster learning; second, we characterize the action-generalization gap (the difference in learning performance between DQN and the expert) in different domains. We find that DQN can indeed generalize over actions in several simple domains, but that its ability to do so decreases as the action space grows larger.