Kavosh Asadi
C-3DPO: Constrained Controlled Classification for Direct Preference Optimization
Feb 22, 2025Abstract:Direct preference optimization (DPO)-style algorithms have emerged as a promising approach for solving the alignment problem in AI. We present a novel perspective that formulates these algorithms as implicit classification algorithms. This classification framework enables us to recover many variants of DPO-style algorithms by choosing appropriate classification labels and loss functions. We then leverage this classification framework to demonstrate that the underlying problem solved in these algorithms is under-specified, making them susceptible to probability collapse of the winner-loser responses. We address this by proposing a set of constraints designed to control the movement of probability mass between the winner and loser in the reference and target policies. Our resulting algorithm, which we call Constrained Controlled Classification DPO (\texttt{C-3DPO}), has a meaningful RLHF interpretation. By hedging against probability collapse, \texttt{C-3DPO} provides practical improvements over vanilla \texttt{DPO} when aligning several large language models using standard preference datasets.
Adjoint sharding for very long context training of state space models
Jan 01, 2025



Abstract:Despite very fast progress, efficiently training large language models (LLMs) in very long contexts remains challenging. Existing methods fall back to training LLMs with short contexts (a maximum of a few thousands tokens in training) and use inference time techniques when evaluating on long contexts (above 1M tokens context window at inference). As opposed to long-context-inference, training on very long context input prompts is quickly limited by GPU memory availability and by the prohibitively long training times it requires on state-of-the-art hardware. Meanwhile, many real-life applications require not only inference but also training/fine-tuning with long context on specific tasks. Such applications include, for example, augmenting the context with various sources of raw reference information for fact extraction, fact summarization, or fact reconciliation tasks. We propose adjoint sharding, a novel technique that comprises sharding gradient calculation during training to reduce memory requirements by orders of magnitude, making training on very long context computationally tractable. Adjoint sharding is based on the adjoint method and computes equivalent gradients to backpropagation. We also propose truncated adjoint sharding to speed up the algorithm while maintaining performance. We provide a distributed version, and a paralleled version of adjoint sharding to further speed up training. Empirical results show the proposed adjoint sharding algorithm reduces memory usage by up to 3X with a 1.27B parameter large language model on 1M context length training. This allows to increase the maximum context length during training or fine-tuning of a 1.27B parameter model from 35K tokens to above 100K tokens on a training infrastructure composed of five AWS P4 instances.
Learning the Target Network in Function Space
Jun 03, 2024



Abstract:We focus on the task of learning the value function in the reinforcement learning (RL) setting. This task is often solved by updating a pair of online and target networks while ensuring that the parameters of these two networks are equivalent. We propose Lookahead-Replicate (LR), a new value-function approximation algorithm that is agnostic to this parameter-space equivalence. Instead, the LR algorithm is designed to maintain an equivalence between the two networks in the function space. This value-based equivalence is obtained by employing a new target-network update. We show that LR leads to a convergent behavior in learning the value function. We also present empirical results demonstrating that LR-based target-network updates significantly improve deep RL on the Atari benchmark.
TAIL: Task-specific Adapters for Imitation Learning with Large Pretrained Models
Oct 09, 2023



Abstract:The full potential of large pretrained models remains largely untapped in control domains like robotics. This is mainly because of the scarcity of data and the computational challenges associated with training or fine-tuning these large models for such applications. Prior work mainly emphasizes effective pretraining of large models for decision-making, with little exploration into how to perform data-efficient continual adaptation of these models for new tasks. Recognizing these constraints, we introduce TAIL (Task-specific Adapters for Imitation Learning), a framework for efficient adaptation to new control tasks. Inspired by recent advancements in parameter-efficient fine-tuning in language domains, we explore efficient fine-tuning techniques -- e.g., Bottleneck Adapters, P-Tuning, and Low-Rank Adaptation (LoRA) -- in TAIL to adapt large pretrained models for new tasks with limited demonstration data. Our extensive experiments in large-scale language-conditioned manipulation tasks comparing prevalent parameter-efficient fine-tuning techniques and adaptation baselines suggest that TAIL with LoRA can achieve the best post-adaptation performance with only 1\% of the trainable parameters of full fine-tuning, while avoiding catastrophic forgetting and preserving adaptation plasticity in continual learning settings.
Resetting the Optimizer in Deep RL: An Empirical Study
Jun 30, 2023



Abstract:We focus on the task of approximating the optimal value function in deep reinforcement learning. This iterative process is comprised of approximately solving a sequence of optimization problems where the objective function can change per iteration. The common approach to solving the problem is to employ modern variants of the stochastic gradient descent algorithm such as Adam. These optimizers maintain their own internal parameters such as estimates of the first and the second moment of the gradient, and update these parameters over time. Therefore, information obtained in previous iterations is being used to solve the optimization problem in the current iteration. We hypothesize that this can contaminate the internal parameters of the employed optimizer in situations where the optimization landscape of the previous iterations is quite different from the current iteration. To hedge against this effect, a simple idea is to reset the internal parameters of the optimizer when starting a new iteration. We empirically investigate this resetting strategy by employing various optimizers in conjunction with the Rainbow algorithm. We demonstrate that this simple modification unleashes the true potential of modern optimizers, and significantly improves the performance of deep RL on the Atari benchmark.
TD Convergence: An Optimization Perspective
Jun 30, 2023
Abstract:We study the convergence behavior of the celebrated temporal-difference (TD) learning algorithm. By looking at the algorithm through the lens of optimization, we first argue that TD can be viewed as an iterative optimization algorithm where the function to be minimized changes per iteration. By carefully investigating the divergence displayed by TD on a classical counter example, we identify two forces that determine the convergent or divergent behavior of the algorithm. We next formalize our discovery in the linear TD setting with quadratic loss and prove that convergence of TD hinges on the interplay between these two forces. We extend this optimization perspective to prove convergence of TD in a much broader setting than just linear approximation and squared loss. Our results provide a theoretical explanation for the successful application of TD in reinforcement learning.
Characterizing the Action-Generalization Gap in Deep Q-Learning
May 11, 2022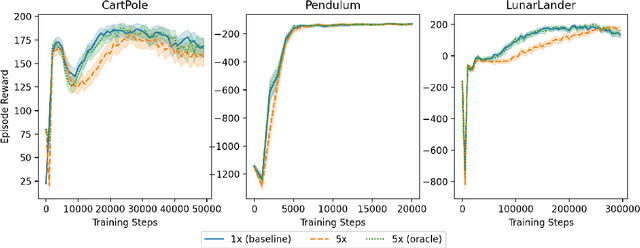
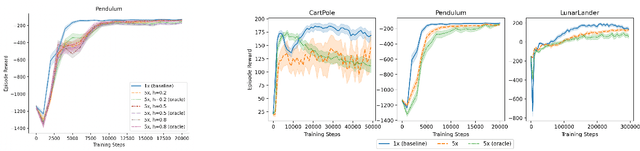
Abstract:We study the action generalization ability of deep Q-learning in discrete action spaces. Generalization is crucial for efficient reinforcement learning (RL) because it allows agents to use knowledge learned from past experiences on new tasks. But while function approximation provides deep RL agents with a natural way to generalize over state inputs, the same generalization mechanism does not apply to discrete action outputs. And yet, surprisingly, our experiments indicate that Deep Q-Networks (DQN), which use exactly this type of function approximator, are still able to achieve modest action generalization. Our main contribution is twofold: first, we propose a method of evaluating action generalization using expert knowledge of action similarity, and empirically confirm that action generalization leads to faster learning; second, we characterize the action-generalization gap (the difference in learning performance between DQN and the expert) in different domains. We find that DQN can indeed generalize over actions in several simple domains, but that its ability to do so decreases as the action space grows larger.
Deep Q-Network with Proximal Iteration
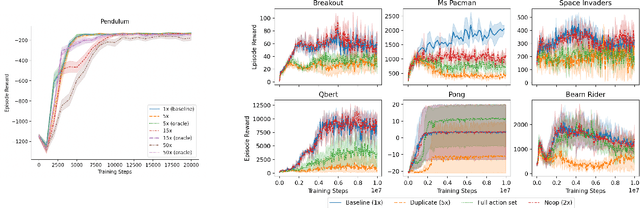
Dec 10, 2021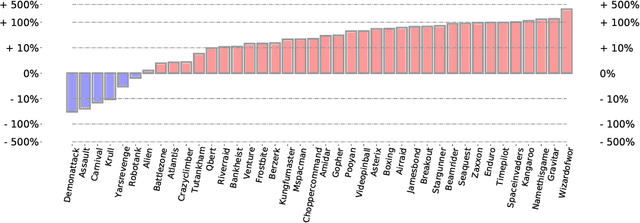

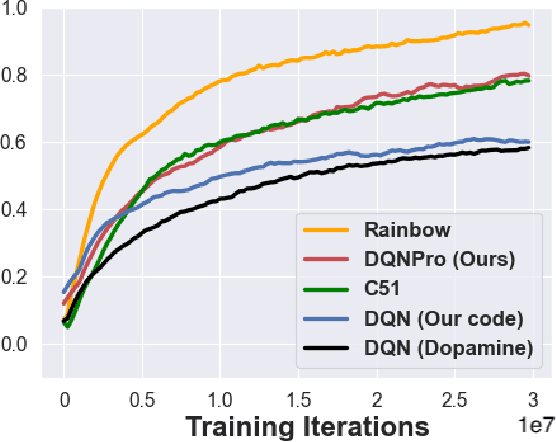

Abstract:We employ Proximal Iteration for value-function optimization in reinforcement learning. Proximal Iteration is a computationally efficient technique that enables us to bias the optimization procedure towards more desirable solutions. As a concrete application of Proximal Iteration in deep reinforcement learning, we endow the objective function of the Deep Q-Network (DQN) agent with a proximal term to ensure that the online-network component of DQN remains in the vicinity of the target network. The resultant agent, which we call DQN with Proximal Iteration, or DQNPro, exhibits significant improvements over the original DQN on the Atari benchmark. Our results accentuate the power of employing sound optimization techniques for deep reinforcement learning.
Coarse-Grained Smoothness for RL in Metric Spaces
Oct 23, 2021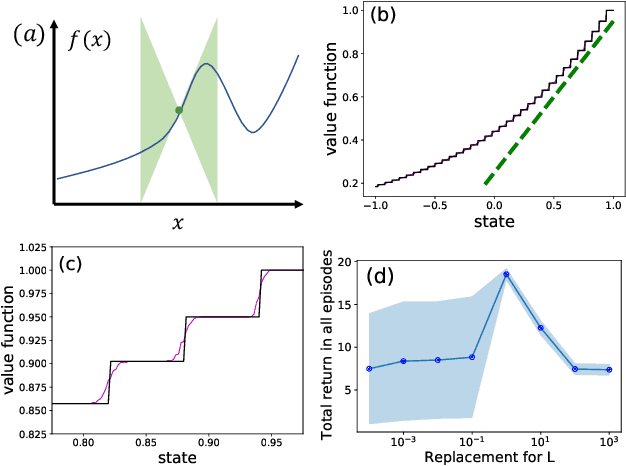
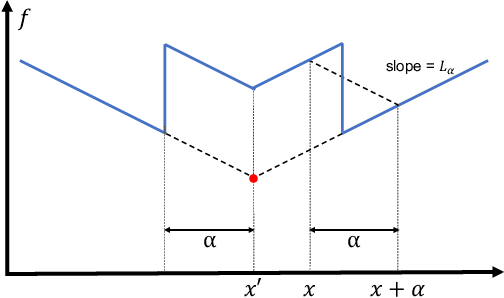
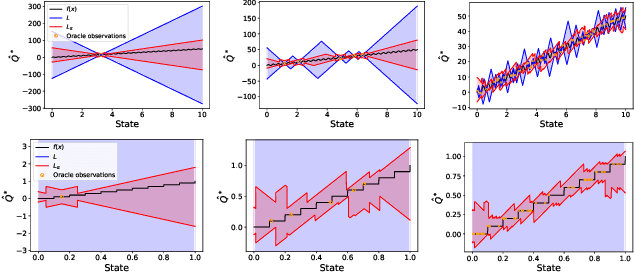
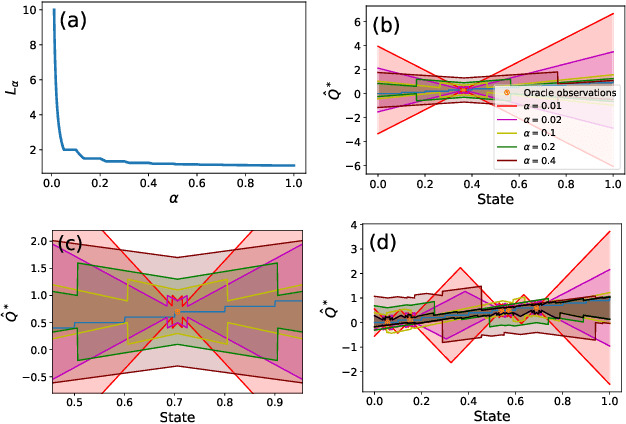
Abstract:Principled decision-making in continuous state--action spaces is impossible without some assumptions. A common approach is to assume Lipschitz continuity of the Q-function. We show that, unfortunately, this property fails to hold in many typical domains. We propose a new coarse-grained smoothness definition that generalizes the notion of Lipschitz continuity, is more widely applicable, and allows us to compute significantly tighter bounds on Q-functions, leading to improved learning. We provide a theoretical analysis of our new smoothness definition, and discuss its implications and impact on control and exploration in continuous domains.
Convergence of a Human-in-the-Loop Policy-Gradient Algorithm With Eligibility Trace Under Reward, Policy, and Advantage Feedback
Sep 15, 2021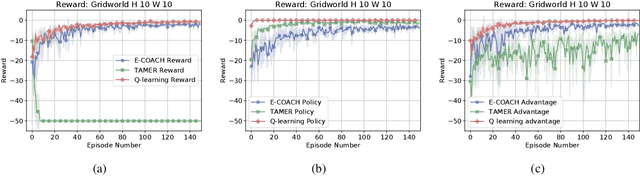

Abstract:Fluid human-agent communication is essential for the future of human-in-the-loop reinforcement learning. An agent must respond appropriately to feedback from its human trainer even before they have significant experience working together. Therefore, it is important that learning agents respond well to various feedback schemes human trainers are likely to provide. This work analyzes the COnvergent Actor-Critic by Humans (COACH) algorithm under three different types of feedback-policy feedback, reward feedback, and advantage feedback. For these three feedback types, we find that COACH can behave sub-optimally. We propose a variant of COACH, episodic COACH (E-COACH), which we prove converges for all three types. We compare our COACH variant with two other reinforcement-learning algorithms: Q-learning and TAMER.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge