Benchmarking Partial Observability in Reinforcement Learning with a Suite of Memory-Improvable Domains

Mitigating partial observability is a necessary but challenging task for general reinforcement learning algorithms. To improve an algorithm's ability to mitigate partial observability, researchers need comprehensive benchmarks to gauge progress. Most algorithms tackling partial observability are only evaluated on benchmarks with simple forms of state aliasing, such as feature masking and Gaussian noise. Such benchmarks do not represent the many forms of partial observability seen in real domains, like visual occlusion or unknown opponent intent. We argue that a partially observable benchmark should have two key properties. The first is coverage in its forms of partial observability, to ensure an algorithm's generalizability. The second is a large gap between the performance of a agents with more or less state information, all other factors roughly equal. This gap implies that an environment is memory improvable: where performance gains in a domain are from an algorithm's ability to cope with partial observability as opposed to other factors. We introduce best-practice guidelines for empirically benchmarking reinforcement learning under partial observability, as well as the open-source library POBAX: Partially Observable Benchmarks in JAX. We characterize the types of partial observability present in various environments and select representative environments for our benchmark. These environments include localization and mapping, visual control, games, and more. Additionally, we show that these tasks are all memory improvable and require hard-to-learn memory functions, providing a concrete signal for partial observability research. This framework includes recommended hyperparameters as well as algorithm implementations for fast, out-of-the-box evaluation, as well as highly performant environments implemented in JAX for GPU-scalable experimentation.

Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy

Reinforcement learning algorithms typically rely on the assumption that the environment dynamics and value function can be expressed in terms of a Markovian state representation. However, when state information is only partially observable, how can an agent learn such a state representation, and how can it detect when it has found one? We introduce a metric that can accomplish both objectives, without requiring access to--or knowledge of--an underlying, unobservable state space. Our metric, the $\lambda$-discrepancy, is the difference between two distinct temporal difference (TD) value estimates, each computed using TD($\lambda$) with a different value of $\lambda$. Since TD($\lambda$=0) makes an implicit Markov assumption and TD($\lambda$=1) does not, a discrepancy between these estimates is a potential indicator of a non-Markovian state representation. Indeed, we prove that the $\lambda$-discrepancy is exactly zero for all Markov decision processes and almost always non-zero for a broad class of partially observable environments. We also demonstrate empirically that, once detected, minimizing the $\lambda$-discrepancy can help with learning a memory function to mitigate the corresponding partial observability. We then train a reinforcement learning agent that simultaneously constructs two recurrent value networks with different $\lambda$ parameters and minimizes the difference between them as an auxiliary loss. The approach scales to challenging partially observable domains, where the resulting agent frequently performs significantly better (and never performs worse) than a baseline recurrent agent with only a single value network.

Evidence of Learned Look-Ahead in a Chess-Playing Neural Network

Do neural networks learn to implement algorithms such as look-ahead or search "in the wild"? Or do they rely purely on collections of simple heuristics? We present evidence of learned look-ahead in the policy network of Leela Chess Zero, the currently strongest neural chess engine. We find that Leela internally represents future optimal moves and that these representations are crucial for its final output in certain board states. Concretely, we exploit the fact that Leela is a transformer that treats every chessboard square like a token in language models, and give three lines of evidence (1) activations on certain squares of future moves are unusually important causally; (2) we find attention heads that move important information "forward and backward in time," e.g., from squares of future moves to squares of earlier ones; and (3) we train a simple probe that can predict the optimal move 2 turns ahead with 92% accuracy (in board states where Leela finds a single best line). These findings are an existence proof of learned look-ahead in neural networks and might be a step towards a better understanding of their capabilities.

Characterizing the Action-Generalization Gap in Deep Q-Learning

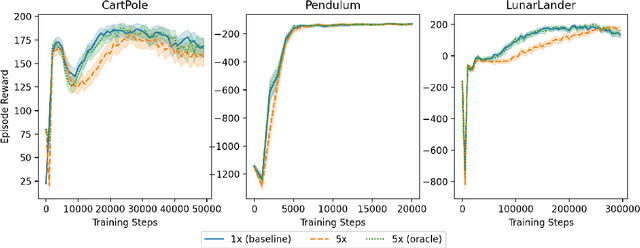
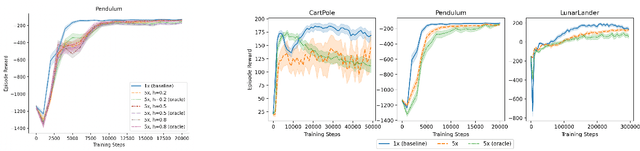
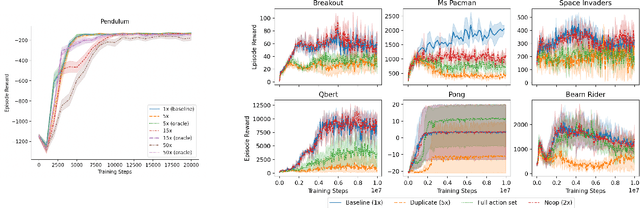
We study the action generalization ability of deep Q-learning in discrete action spaces. Generalization is crucial for efficient reinforcement learning (RL) because it allows agents to use knowledge learned from past experiences on new tasks. But while function approximation provides deep RL agents with a natural way to generalize over state inputs, the same generalization mechanism does not apply to discrete action outputs. And yet, surprisingly, our experiments indicate that Deep Q-Networks (DQN), which use exactly this type of function approximator, are still able to achieve modest action generalization. Our main contribution is twofold: first, we propose a method of evaluating action generalization using expert knowledge of action similarity, and empirically confirm that action generalization leads to faster learning; second, we characterize the action-generalization gap (the difference in learning performance between DQN and the expert) in different domains. We find that DQN can indeed generalize over actions in several simple domains, but that its ability to do so decreases as the action space grows larger.

Coarse-Grained Smoothness for RL in Metric Spaces

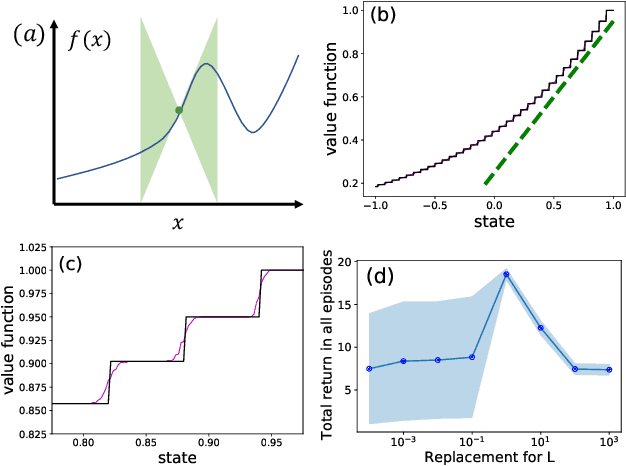
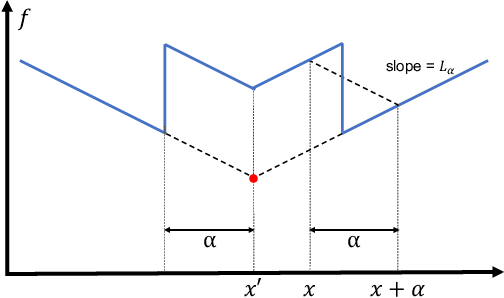
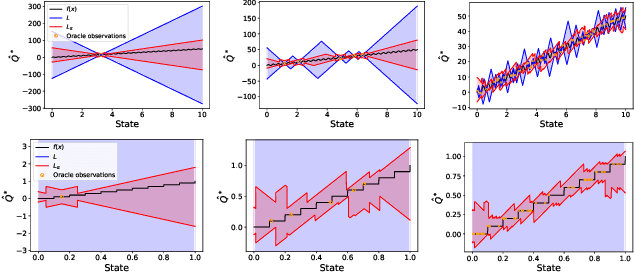
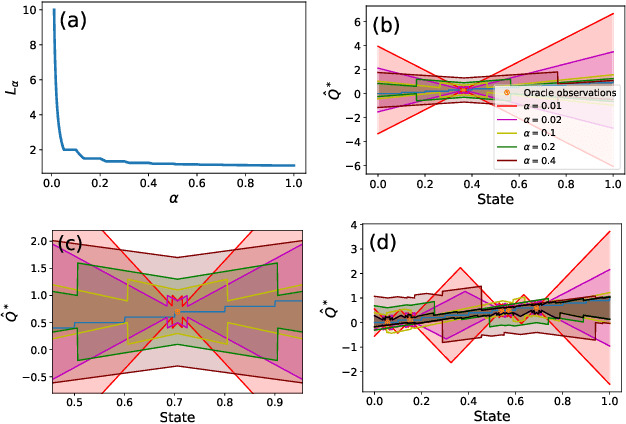
Principled decision-making in continuous state--action spaces is impossible without some assumptions. A common approach is to assume Lipschitz continuity of the Q-function. We show that, unfortunately, this property fails to hold in many typical domains. We propose a new coarse-grained smoothness definition that generalizes the notion of Lipschitz continuity, is more widely applicable, and allows us to compute significantly tighter bounds on Q-functions, leading to improved learning. We provide a theoretical analysis of our new smoothness definition, and discuss its implications and impact on control and exploration in continuous domains.

Bad-Policy Density: A Measure of Reinforcement Learning Hardness

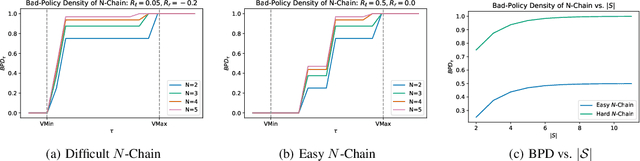
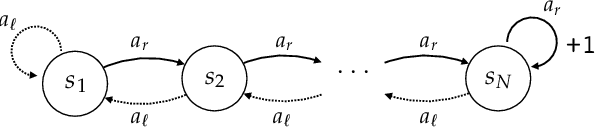
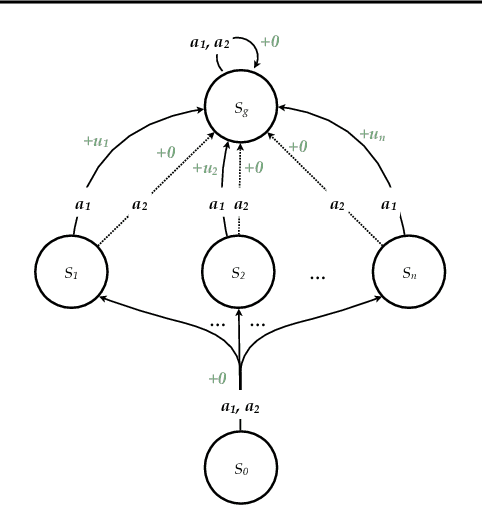
Reinforcement learning is hard in general. Yet, in many specific environments, learning is easy. What makes learning easy in one environment, but difficult in another? We address this question by proposing a simple measure of reinforcement-learning hardness called the bad-policy density. This quantity measures the fraction of the deterministic stationary policy space that is below a desired threshold in value. We prove that this simple quantity has many properties one would expect of a measure of learning hardness. Further, we prove it is NP-hard to compute the measure in general, but there are paths to polynomial-time approximation. We conclude by summarizing potential directions and uses for this measure.

Learning Markov State Abstractions for Deep Reinforcement Learning

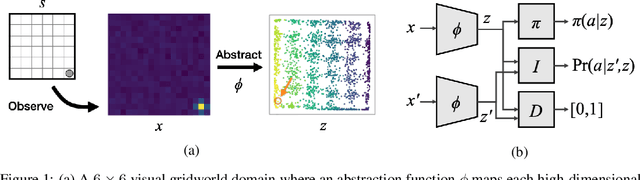
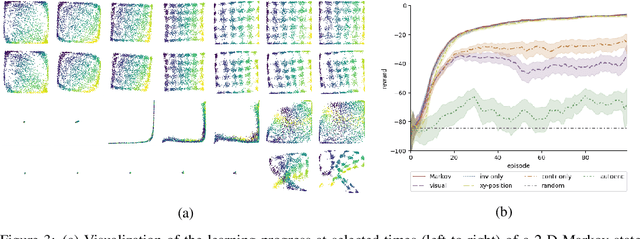
The fundamental assumption of reinforcement learning in Markov decision processes (MDPs) is that the relevant decision process is, in fact, Markov. However, when MDPs have rich observations, agents typically learn by way of an abstract state representation, and such representations are not guaranteed to preserve the Markov property. We introduce a novel set of conditions and prove that they are sufficient for learning a Markov abstract state representation. We then describe a practical training procedure that combines inverse model estimation and temporal contrastive learning to learn an abstraction that approximately satisfies these conditions. Our novel training objective is compatible with both online and offline training: it does not require a reward signal, but agents can capitalize on reward information when available. We empirically evaluate our approach on a visual gridworld domain and a set of continuous control benchmarks. Our approach learns representations that capture the underlying structure of the domain and lead to improved sample efficiency over state-of-the-art deep reinforcement learning with visual features -- often matching or exceeding the performance achieved with hand-designed compact state information.

Finding Macro-Actions with Disentangled Effects for Efficient Planning with the Goal-Count Heuristic

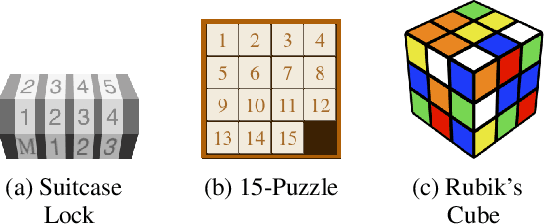
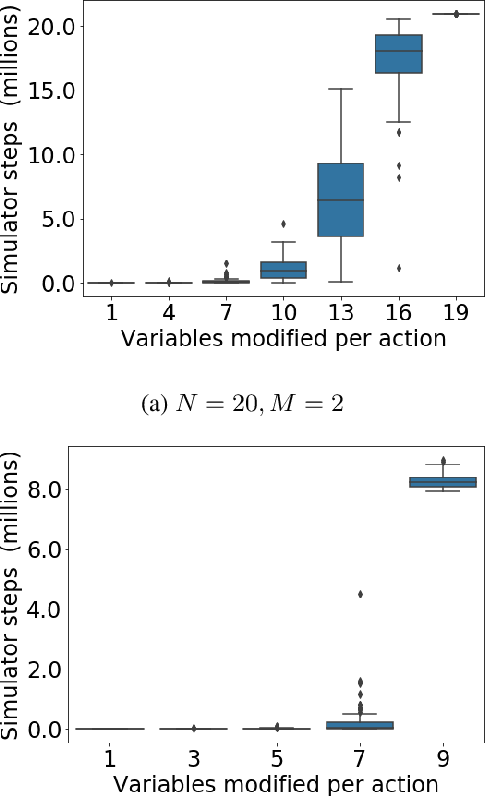
The difficulty of classical planning increases exponentially with search-tree depth. Heuristic search can make planning more efficient, but good heuristics often require domain-specific assumptions and may not generalize to new problems. Rather than treating the planning problem as fixed and carefully designing a heuristic to match it, we instead construct macro-actions that support efficient planning with the simple and general-purpose "goal-count" heuristic. Our approach searches for macro-actions that modify only a small number of state variables (we call this measure "entanglement"). We show experimentally that reducing entanglement exponentially decreases planning time with the goal-count heuristic. Our method discovers macro-actions with disentangled effects that dramatically improve planning efficiency for 15-puzzle and Rubik's cube, reliably solving each domain without prior knowledge, and solving Rubik's cube with orders of magnitude less data than competing approaches.