Structure-Informed Deep Reinforcement Learning for Inventory Management

This paper investigates the application of Deep Reinforcement Learning (DRL) to classical inventory management problems, with a focus on practical implementation considerations. We apply a DRL algorithm based on DirectBackprop to several fundamental inventory management scenarios including multi-period systems with lost sales (with and without lead times), perishable inventory management, dual sourcing, and joint inventory procurement and removal. The DRL approach learns policies across products using only historical information that would be available in practice, avoiding unrealistic assumptions about demand distributions or access to distribution parameters. We demonstrate that our generic DRL implementation performs competitively against or outperforms established benchmarks and heuristics across these diverse settings, while requiring minimal parameter tuning. Through examination of the learned policies, we show that the DRL approach naturally captures many known structural properties of optimal policies derived from traditional operations research methods. To further improve policy performance and interpretability, we propose a Structure-Informed Policy Network technique that explicitly incorporates analytically-derived characteristics of optimal policies into the learning process. This approach can help interpretability and add robustness to the policy in out-of-sample performance, as we demonstrate in an example with realistic demand data. Finally, we provide an illustrative application of DRL in a non-stationary setting. Our work bridges the gap between data-driven learning and analytical insights in inventory management while maintaining practical applicability.

Geometry of Neural Reinforcement Learning in Continuous State and Action Spaces

Advances in reinforcement learning (RL) have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens to understand the locally attained set of states. The set of all parametrised policies learnt through a semi-gradient based approach induces a set of attainable states in RL. We show that the training dynamics of a two-layer neural policy induce a low dimensional manifold of attainable states embedded in the high-dimensional nominal state space trained using an actor-critic algorithm. We prove that, under certain conditions, the dimensionality of this manifold is of the order of the dimensionality of the action space. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments and also demonstrate the results in a toy environment with varying dimensionality. We also show the applicability of this theoretical result by introducing a local manifold learning layer to the policy and value function networks to improve the performance in control environments with very high degrees of freedom by changing one layer of the neural network to learn sparse representations.

Mitigating Partial Observability in Sequential Decision Processes via the Lambda Discrepancy

Reinforcement learning algorithms typically rely on the assumption that the environment dynamics and value function can be expressed in terms of a Markovian state representation. However, when state information is only partially observable, how can an agent learn such a state representation, and how can it detect when it has found one? We introduce a metric that can accomplish both objectives, without requiring access to--or knowledge of--an underlying, unobservable state space. Our metric, the $\lambda$-discrepancy, is the difference between two distinct temporal difference (TD) value estimates, each computed using TD($\lambda$) with a different value of $\lambda$. Since TD($\lambda$=0) makes an implicit Markov assumption and TD($\lambda$=1) does not, a discrepancy between these estimates is a potential indicator of a non-Markovian state representation. Indeed, we prove that the $\lambda$-discrepancy is exactly zero for all Markov decision processes and almost always non-zero for a broad class of partially observable environments. We also demonstrate empirically that, once detected, minimizing the $\lambda$-discrepancy can help with learning a memory function to mitigate the corresponding partial observability. We then train a reinforcement learning agent that simultaneously constructs two recurrent value networks with different $\lambda$ parameters and minimizes the difference between them as an auxiliary loss. The approach scales to challenging partially observable domains, where the resulting agent frequently performs significantly better (and never performs worse) than a baseline recurrent agent with only a single value network.

TD Convergence: An Optimization Perspective

We study the convergence behavior of the celebrated temporal-difference (TD) learning algorithm. By looking at the algorithm through the lens of optimization, we first argue that TD can be viewed as an iterative optimization algorithm where the function to be minimized changes per iteration. By carefully investigating the divergence displayed by TD on a classical counter example, we identify two forces that determine the convergent or divergent behavior of the algorithm. We next formalize our discovery in the linear TD setting with quadratic loss and prove that convergence of TD hinges on the interplay between these two forces. We extend this optimization perspective to prove convergence of TD in a much broader setting than just linear approximation and squared loss. Our results provide a theoretical explanation for the successful application of TD in reinforcement learning.

Robust Decision-Focused Learning for Reward Transfer

Decision-focused (DF) model-based reinforcement learning has recently been introduced as a powerful algorithm which can focus on learning the MDP dynamics which are most relevant for obtaining high rewards. While this approach increases the performance of agents by focusing the learning towards optimizing for the reward directly, it does so by learning less accurate dynamics (from a MLE standpoint), and may thus be brittle to changes in the reward function. In this work, we develop the robust decision-focused (RDF) algorithm which leverages the non-identifiability of DF solutions to learn models which maximize expected returns while simultaneously learning models which are robust to changes in the reward function. We demonstrate on a variety of toy example and healthcare simulators that RDF significantly increases the robustness of DF to changes in the reward function, without decreasing the overall return the agent obtains.

On the Geometry of Reinforcement Learning in Continuous State and Action Spaces

Advances in reinforcement learning have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens. Central to our work is the idea that the transition dynamics induce a low dimensional manifold of reachable states embedded in the high-dimensional nominal state space. We prove that, under certain conditions, the dimensionality of this manifold is at most the dimensionality of the action space plus one. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments. We further demonstrate the applicability of our result by learning a policy in this low dimensional representation. To do so we introduce an algorithm that learns a mapping to a low dimensional representation, as a narrow hidden layer of a deep neural network, in tandem with the policy using DDPG. Our experiments show that a policy learnt this way perform on par or better for four MuJoCo control suite tasks.

A Bayesian Approach to Learning Bandit Structure in Markov Decision Processes

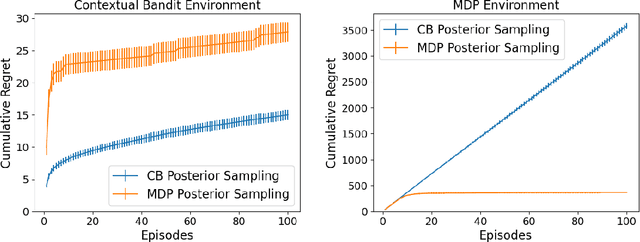
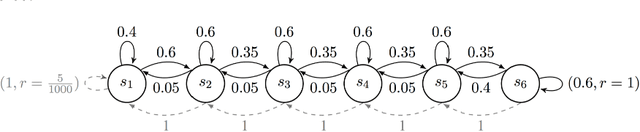
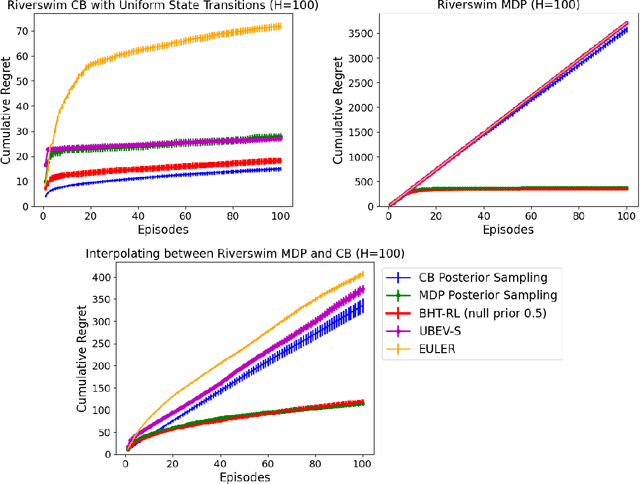
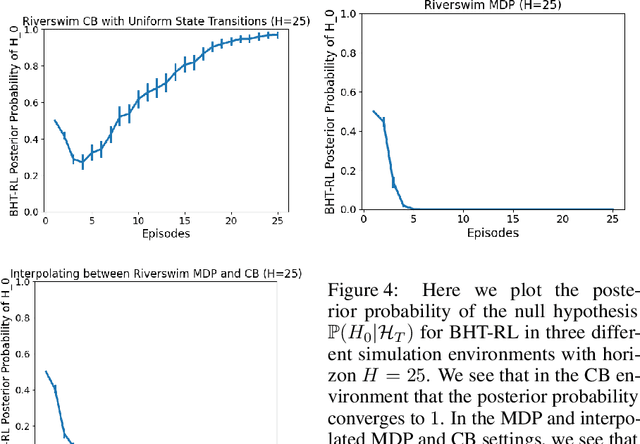
In the reinforcement learning literature, there are many algorithms developed for either Contextual Bandit (CB) or Markov Decision Processes (MDP) environments. However, when deploying reinforcement learning algorithms in the real world, even with domain expertise, it is often difficult to know whether it is appropriate to treat a sequential decision making problem as a CB or an MDP. In other words, do actions affect future states, or only the immediate rewards? Making the wrong assumption regarding the nature of the environment can lead to inefficient learning, or even prevent the algorithm from ever learning an optimal policy, even with infinite data. In this work we develop an online algorithm that uses a Bayesian hypothesis testing approach to learn the nature of the environment. Our algorithm allows practitioners to incorporate prior knowledge about whether the environment is that of a CB or an MDP, and effectively interpolate between classical CB and MDP-based algorithms to mitigate against the effects of misspecifying the environment. We perform simulations and demonstrate that in CB settings our algorithm achieves lower regret than MDP-based algorithms, while in non-bandit MDP settings our algorithm is able to learn the optimal policy, often achieving comparable regret to MDP-based algorithms.

Deep Q-Network with Proximal Iteration

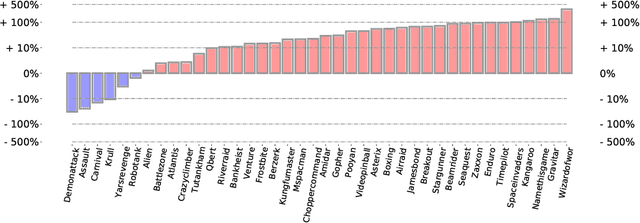
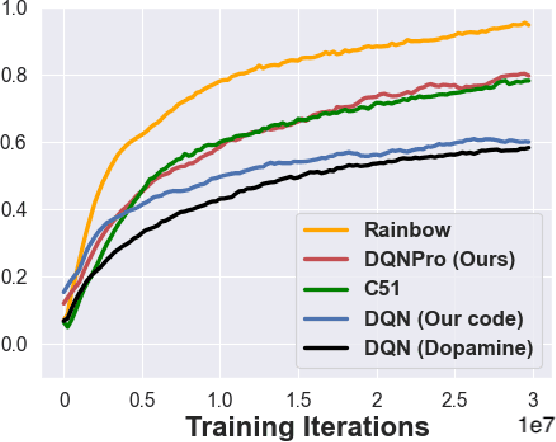
We employ Proximal Iteration for value-function optimization in reinforcement learning. Proximal Iteration is a computationally efficient technique that enables us to bias the optimization procedure towards more desirable solutions. As a concrete application of Proximal Iteration in deep reinforcement learning, we endow the objective function of the Deep Q-Network (DQN) agent with a proximal term to ensure that the online-network component of DQN remains in the vicinity of the target network. The resultant agent, which we call DQN with Proximal Iteration, or DQNPro, exhibits significant improvements over the original DQN on the Atari benchmark. Our results accentuate the power of employing sound optimization techniques for deep reinforcement learning.

Identification of Subgroups With Similar Benefits in Off-Policy Policy Evaluation

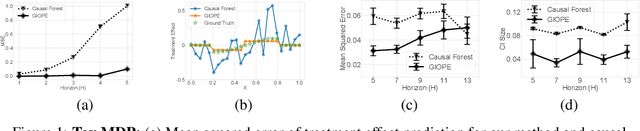
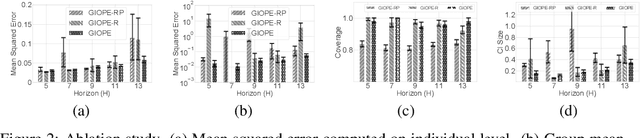
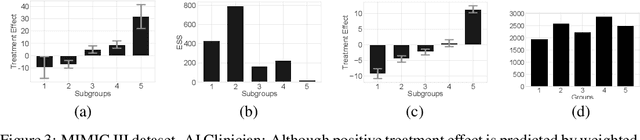
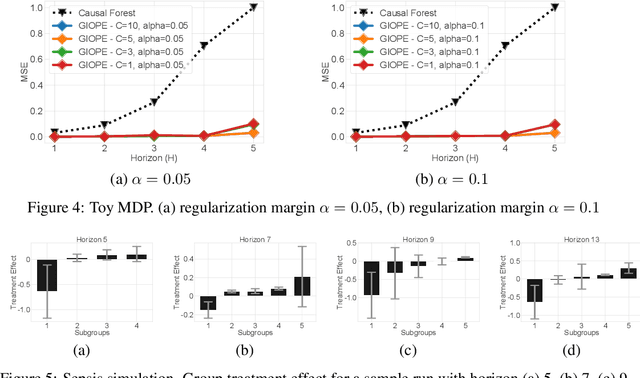
Off-policy policy evaluation methods for sequential decision making can be used to help identify if a proposed decision policy is better than a current baseline policy. However, a new decision policy may be better than a baseline policy for some individuals but not others. This has motivated a push towards personalization and accurate per-state estimates of heterogeneous treatment effects (HTEs). Given the limited data present in many important applications, individual predictions can come at a cost to accuracy and confidence in such predictions. We develop a method to balance the need for personalization with confident predictions by identifying subgroups where it is possible to confidently estimate the expected difference in a new decision policy relative to a baseline. We propose a novel loss function that accounts for uncertainty during the subgroup partitioning phase. In experiments, we show that our method can be used to form accurate predictions of HTEs where other methods struggle.

Coarse-Grained Smoothness for RL in Metric Spaces

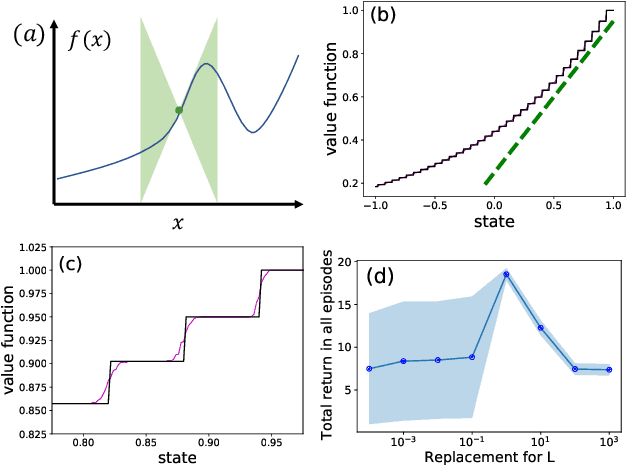
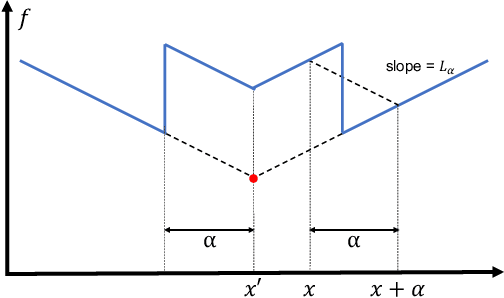
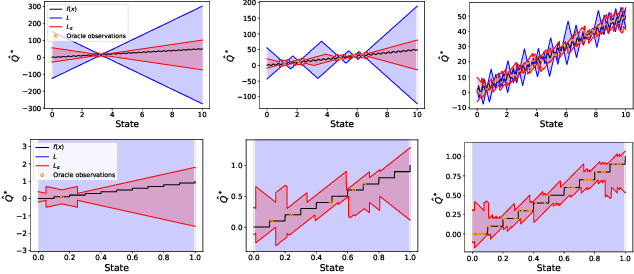
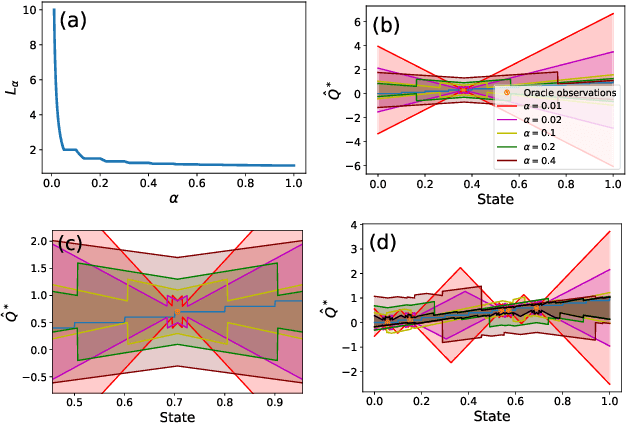
Principled decision-making in continuous state--action spaces is impossible without some assumptions. A common approach is to assume Lipschitz continuity of the Q-function. We show that, unfortunately, this property fails to hold in many typical domains. We propose a new coarse-grained smoothness definition that generalizes the notion of Lipschitz continuity, is more widely applicable, and allows us to compute significantly tighter bounds on Q-functions, leading to improved learning. We provide a theoretical analysis of our new smoothness definition, and discuss its implications and impact on control and exploration in continuous domains.