Energy-Aware, Collision-Free Information Gathering for Heterogeneous Robot Teams

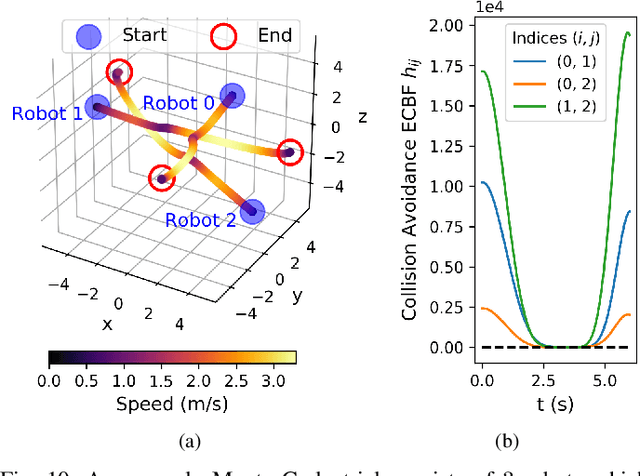
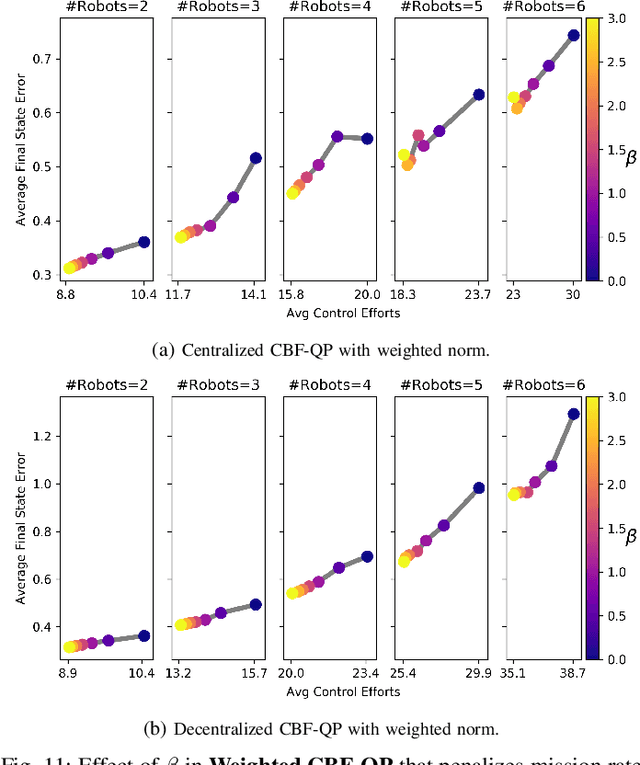
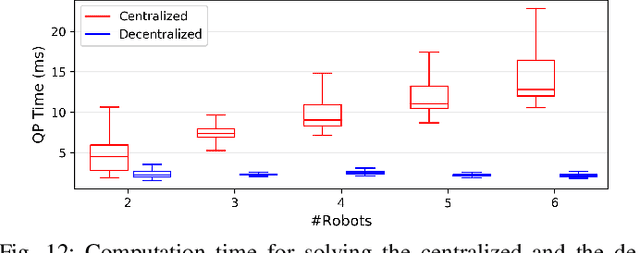
This paper considers the problem of safely coordinating a team of sensor-equipped robots to reduce uncertainty about a dynamical process, where the objective trades off information gain and energy cost. Optimizing this trade-off is desirable, but leads to a non-monotone objective function in the set of robot trajectories. Therefore, common multi-robot planners based on coordinate descent lose their performance guarantees. Furthermore, methods that handle non-monotonicity lose their performance guarantees when subject to inter-robot collision avoidance constraints. As it is desirable to retain both the performance guarantee and safety guarantee, this work proposes a hierarchical approach with a distributed planner that uses local search with a worst-case performance guarantees and a decentralized controller based on control barrier functions that ensures safety and encourages timely arrival at sensing locations. Via extensive simulations, hardware-in-the-loop tests and hardware experiments, we demonstrate that the proposed approach achieves a better trade-off between sensing and energy cost than coordinate descent based algorithms.

Probable Domain Generalization via Quantile Risk Minimization

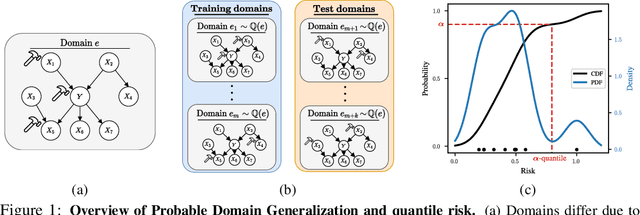
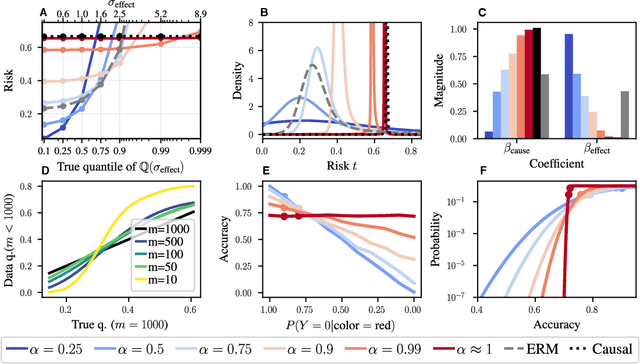
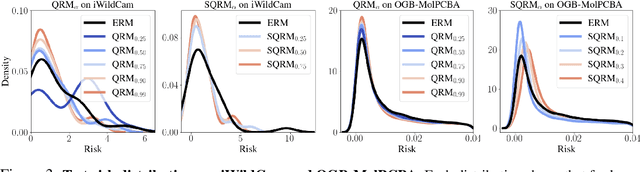
Domain generalization (DG) seeks predictors which perform well on unseen test distributions by leveraging labeled training data from multiple related distributions or domains. To achieve this, the standard formulation optimizes for worst-case performance over the set of all possible domains. However, with worst-case shifts very unlikely in practice, this generally leads to overly-conservative solutions. In fact, a recent study found that no DG algorithm outperformed empirical risk minimization in terms of average performance. In this work, we argue that DG is neither a worst-case problem nor an average-case problem, but rather a probabilistic one. To this end, we propose a probabilistic framework for DG, which we call Probable Domain Generalization, wherein our key idea is that distribution shifts seen during training should inform us of probable shifts at test time. To realize this, we explicitly relate training and test domains as draws from the same underlying meta-distribution, and propose a new optimization problem -- Quantile Risk Minimization (QRM) -- which requires that predictors generalize with high probability. We then prove that QRM: (i) produces predictors that generalize to new domains with a desired probability, given sufficiently many domains and samples; and (ii) recovers the causal predictor as the desired probability of generalization approaches one. In our experiments, we introduce a more holistic quantile-focused evaluation protocol for DG, and show that our algorithms outperform state-of-the-art baselines on real and synthetic data.

NOMAD: Nonlinear Manifold Decoders for Operator Learning

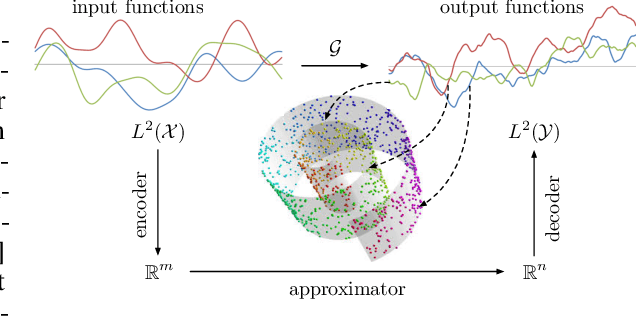
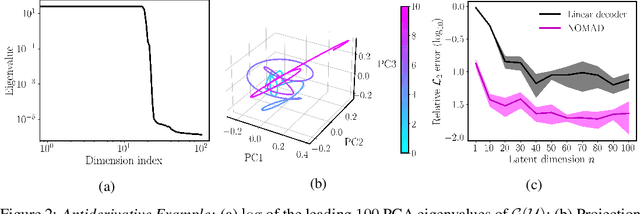
Supervised learning in function spaces is an emerging area of machine learning research with applications to the prediction of complex physical systems such as fluid flows, solid mechanics, and climate modeling. By directly learning maps (operators) between infinite dimensional function spaces, these models are able to learn discretization invariant representations of target functions. A common approach is to represent such target functions as linear combinations of basis elements learned from data. However, there are simple scenarios where, even though the target functions form a low dimensional submanifold, a very large number of basis elements is needed for an accurate linear representation. Here we present NOMAD, a novel operator learning framework with a nonlinear decoder map capable of learning finite dimensional representations of nonlinear submanifolds in function spaces. We show this method is able to accurately learn low dimensional representations of solution manifolds to partial differential equations while outperforming linear models of larger size. Additionally, we compare to state-of-the-art operator learning methods on a complex fluid dynamics benchmark and achieve competitive performance with a significantly smaller model size and training cost.

Collaborative Linear Bandits with Adversarial Agents: Near-Optimal Regret Bounds

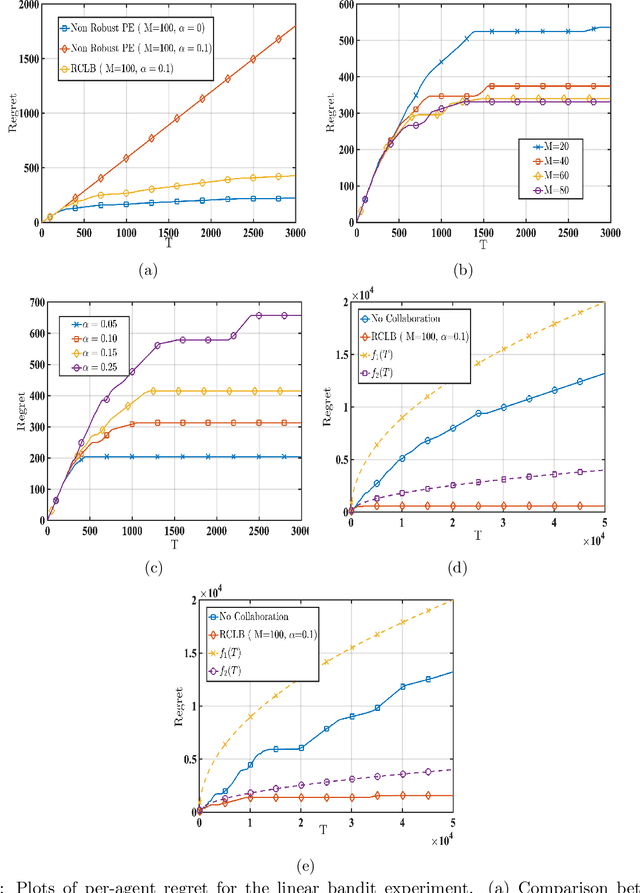
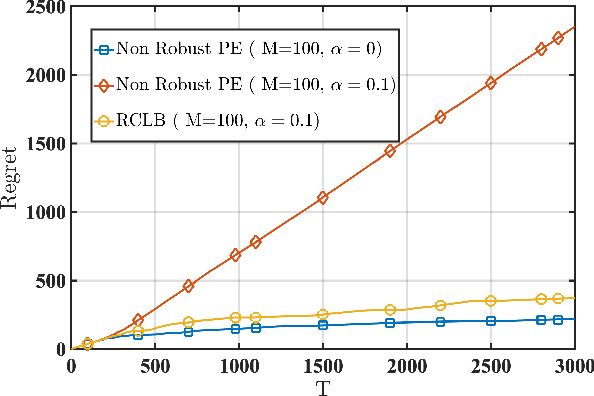
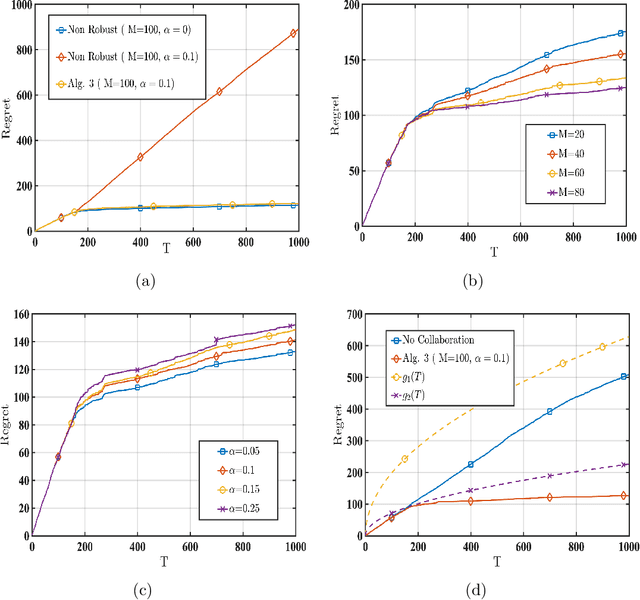
We consider a linear stochastic bandit problem involving $M$ agents that can collaborate via a central server to minimize regret. A fraction $\alpha$ of these agents are adversarial and can act arbitrarily, leading to the following tension: while collaboration can potentially reduce regret, it can also disrupt the process of learning due to adversaries. In this work, we provide a fundamental understanding of this tension by designing new algorithms that balance the exploration-exploitation trade-off via carefully constructed robust confidence intervals. We also complement our algorithms with tight analyses. First, we develop a robust collaborative phased elimination algorithm that achieves $\tilde{O}\left(\alpha+ 1/\sqrt{M}\right) \sqrt{dT}$ regret for each good agent; here, $d$ is the model-dimension and $T$ is the horizon. For small $\alpha$, our result thus reveals a clear benefit of collaboration despite adversaries. Using an information-theoretic argument, we then prove a matching lower bound, thereby providing the first set of tight, near-optimal regret bounds for collaborative linear bandits with adversaries. Furthermore, by leveraging recent advances in high-dimensional robust statistics, we significantly extend our algorithmic ideas and results to (i) the generalized linear bandit model that allows for non-linear observation maps; and (ii) the contextual bandit setting that allows for time-varying feature vectors.

Learning to Control Linear Systems can be Hard

In this paper, we study the statistical difficulty of learning to control linear systems. We focus on two standard benchmarks, the sample complexity of stabilization, and the regret of the online learning of the Linear Quadratic Regulator (LQR). Prior results state that the statistical difficulty for both benchmarks scales polynomially with the system state dimension up to system-theoretic quantities. However, this does not reveal the whole picture. By utilizing minimax lower bounds for both benchmarks, we prove that there exist non-trivial classes of systems for which learning complexity scales dramatically, i.e. exponentially, with the system dimension. This situation arises in the case of underactuated systems, i.e. systems with fewer inputs than states. Such systems are structurally difficult to control and their system theoretic quantities can scale exponentially with the system dimension dominating learning complexity. Under some additional structural assumptions (bounding systems away from uncontrollability), we provide qualitatively matching upper bounds. We prove that learning complexity can be at most exponential with the controllability index of the system, that is the degree of underactuation.

Reactive Informative Planning for Mobile Manipulation Tasks under Sensing and Environmental Uncertainty

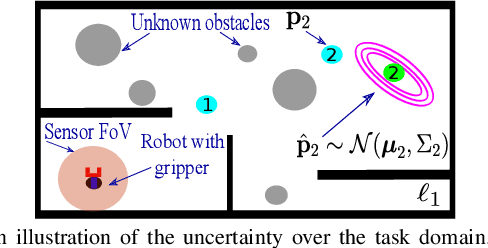
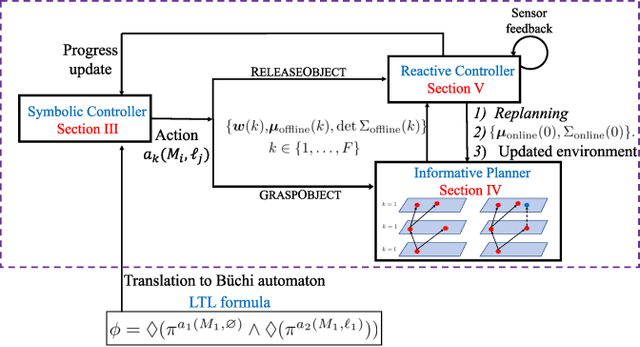
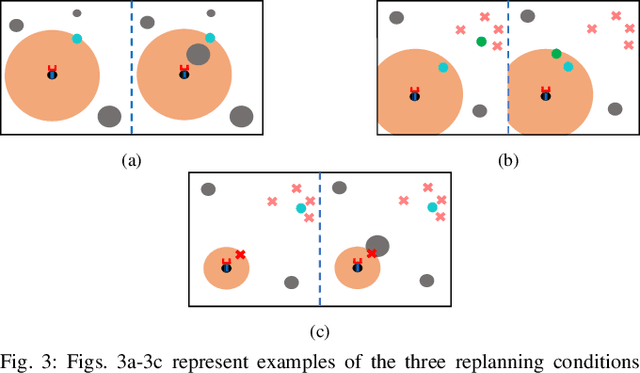
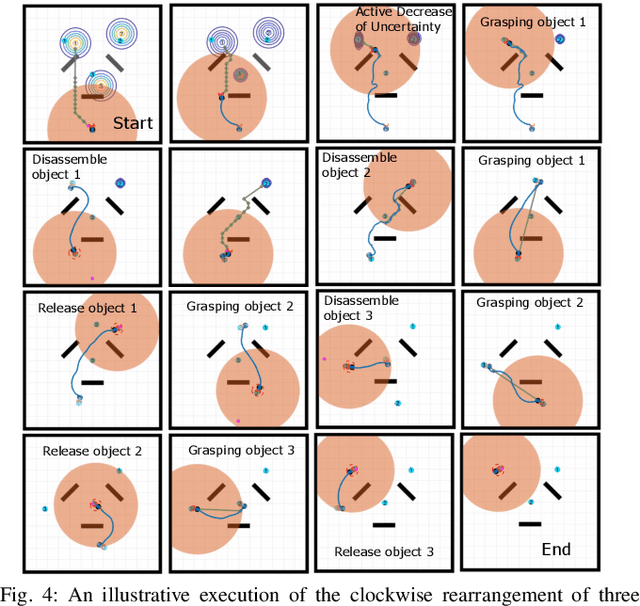
In this paper we address mobile manipulation planning problems in the presence of sensing and environmental uncertainty. In particular, we consider mobile sensing manipulators operating in environments with unknown geometry and uncertain movable objects, while being responsible for accomplishing tasks requiring grasping and releasing objects in a logical fashion. Existing algorithms either do not scale well or neglect sensing and/or environmental uncertainty. To face these challenges, we propose a hybrid control architecture, where a symbolic controller generates high-level manipulation commands (e.g., grasp an object) based on environmental feedback, an informative planner designs paths to actively decrease the uncertainty of objects of interest, and a continuous reactive controller tracks the sparse waypoints comprising the informative paths while avoiding a priori unknown obstacles. The overall architecture can handle environmental and sensing uncertainty online, as the robot explores its workspace. Using numerical simulations, we show that the proposed architecture can handle tasks of increased complexity while responding to unanticipated adverse configurations.

Distributed Statistical Min-Max Learning in the Presence of Byzantine Agents

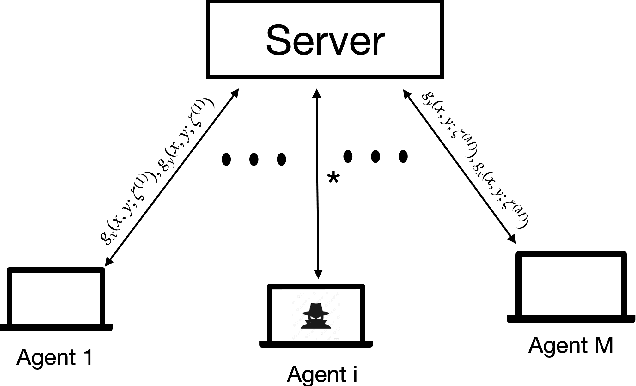
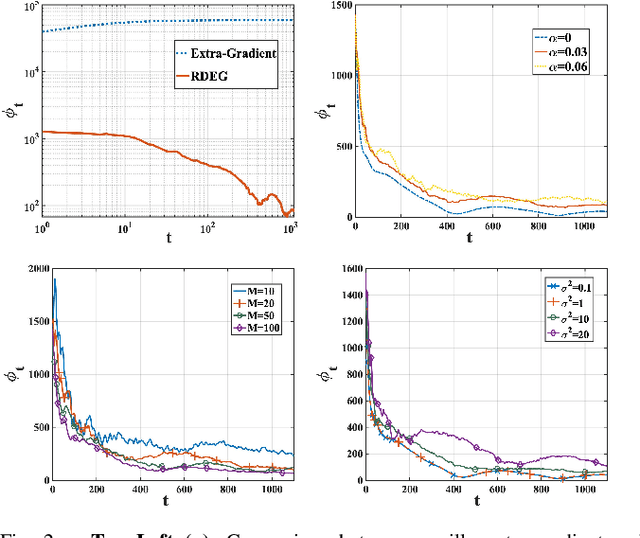
Recent years have witnessed a growing interest in the topic of min-max optimization, owing to its relevance in the context of generative adversarial networks (GANs), robust control and optimization, and reinforcement learning. Motivated by this line of work, we consider a multi-agent min-max learning problem, and focus on the emerging challenge of contending with worst-case Byzantine adversarial agents in such a setup. By drawing on recent results from robust statistics, we design a robust distributed variant of the extra-gradient algorithm - a popular algorithmic approach for min-max optimization. Our main contribution is to provide a crisp analysis of the proposed robust extra-gradient algorithm for smooth convex-concave and smooth strongly convex-strongly concave functions. Specifically, we establish statistical rates of convergence to approximate saddle points. Our rates are near-optimal, and reveal both the effect of adversarial corruption and the benefit of collaboration among the non-faulty agents. Notably, this is the first paper to provide formal theoretical guarantees for large-scale distributed min-max learning in the presence of adversarial agents.

Adaptive Stochastic MPC under Unknown Noise Distribution

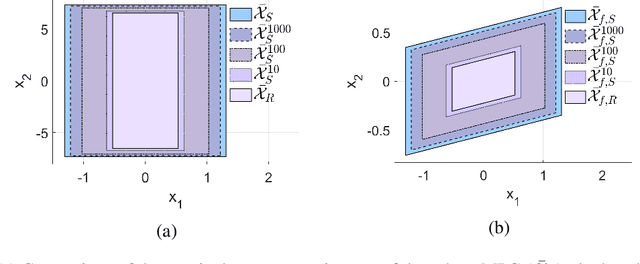
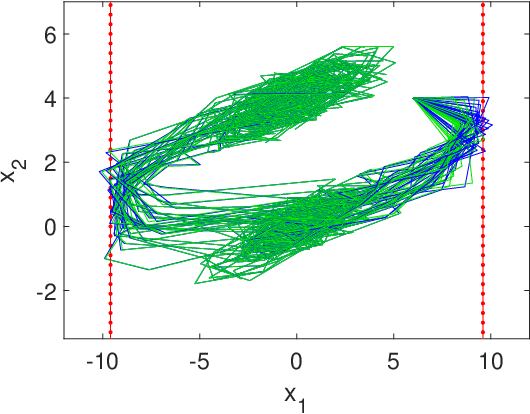
In this paper, we address the stochastic MPC (SMPC) problem for linear systems, subject to chance state constraints and hard input constraints, under unknown noise distribution. First, we reformulate the chance state constraints as deterministic constraints depending only on explicit noise statistics. Based on these reformulated constraints, we design a distributionally robust and robustly stable benchmark SMPC algorithm for the ideal setting of known noise statistics. Then, we employ this benchmark controller to derive a novel robustly stable adaptive SMPC scheme that learns the necessary noise statistics online, while guaranteeing time-uniform satisfaction of the unknown reformulated state constraints with high probability. The latter is achieved through the use of confidence intervals which rely on the empirical noise statistics and are valid uniformly over time. Moreover, control performance is improved over time as more noise samples are gathered and better estimates of the noise statistics are obtained, given the online adaptation of the estimated reformulated constraints. Additionally, in tracking problems with multiple successive targets our approach leads to an online-enlarged domain of attraction compared to robust tube-based MPC. A numerical simulation of a DC-DC converter is used to demonstrate the effectiveness of the developed methodology.

Chordal Sparsity for Lipschitz Constant Estimation of Deep Neural Networks

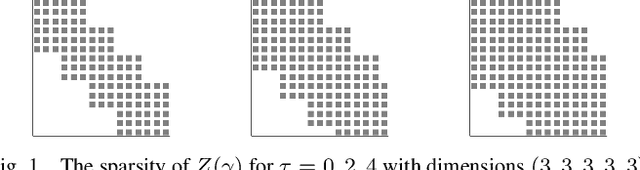
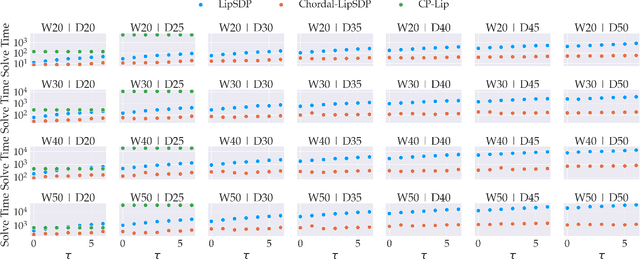
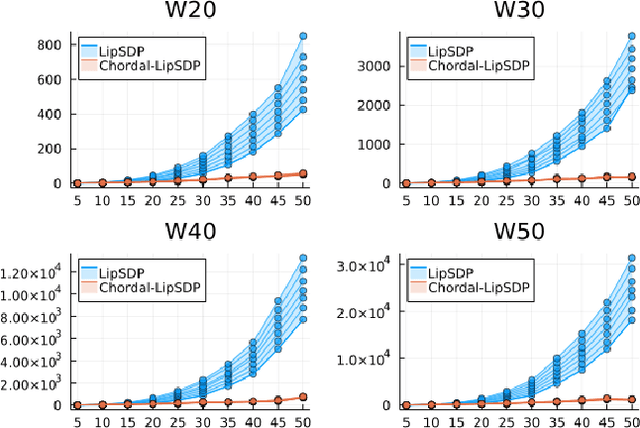
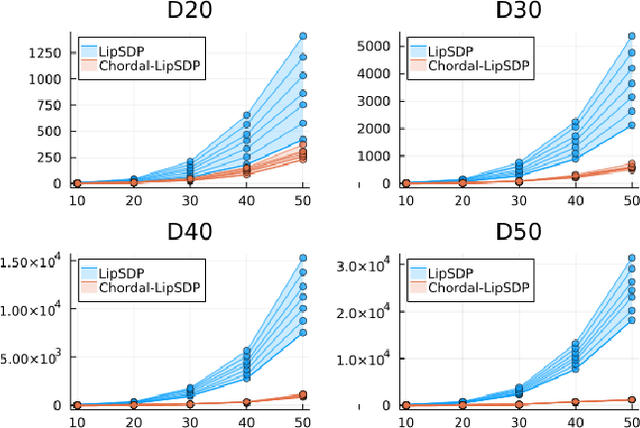
Lipschitz constants of neural networks allow for guarantees of robustness in image classification, safety in controller design, and generalizability beyond the training data. As calculating Lipschitz constants is NP-hard, techniques for estimating Lipschitz constants must navigate the trade-off between scalability and accuracy. In this work, we significantly push the scalability frontier of a semidefinite programming technique known as LipSDP while achieving zero accuracy loss. We first show that LipSDP has chordal sparsity, which allows us to derive a chordally sparse formulation that we call Chordal-LipSDP. The key benefit is that the main computational bottleneck of LipSDP, a large semidefinite constraint, is now decomposed into an equivalent collection of smaller ones: allowing Chordal-LipSDP to outperform LipSDP particularly as the network depth grows. Moreover, our formulation uses a tunable sparsity parameter that enables one to gain tighter estimates without incurring a significant computational cost. We illustrate the scalability of our approach through extensive numerical experiments.

Do Deep Networks Transfer Invariances Across Classes?

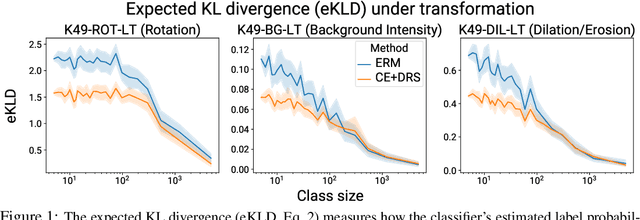
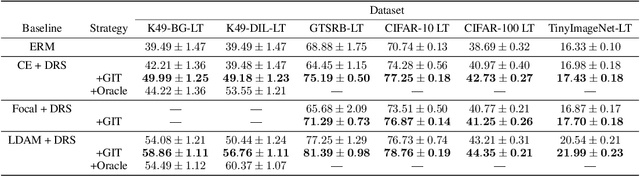
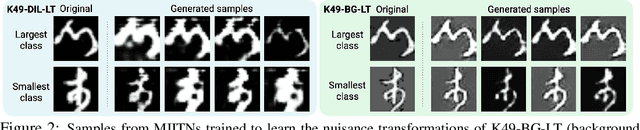
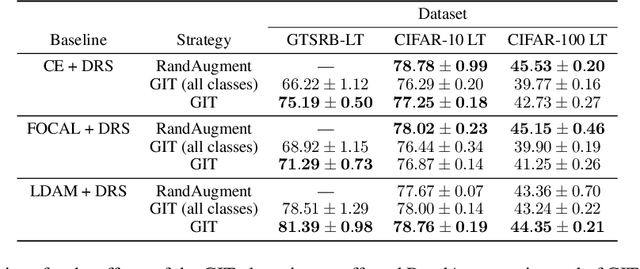
To generalize well, classifiers must learn to be invariant to nuisance transformations that do not alter an input's class. Many problems have "class-agnostic" nuisance transformations that apply similarly to all classes, such as lighting and background changes for image classification. Neural networks can learn these invariances given sufficient data, but many real-world datasets are heavily class imbalanced and contain only a few examples for most of the classes. We therefore pose the question: how well do neural networks transfer class-agnostic invariances learned from the large classes to the small ones? Through careful experimentation, we observe that invariance to class-agnostic transformations is still heavily dependent on class size, with the networks being much less invariant on smaller classes. This result holds even when using data balancing techniques, and suggests poor invariance transfer across classes. Our results provide one explanation for why classifiers generalize poorly on unbalanced and long-tailed distributions. Based on this analysis, we show how a generative approach for learning the nuisance transformations can help transfer invariances across classes and improve performance on a set of imbalanced image classification benchmarks. Source code for our experiments is available at https://github.com/AllanYangZhou/generative-invariance-transfer.