MATT-Diff: Multimodal Active Target Tracking by Diffusion Policy

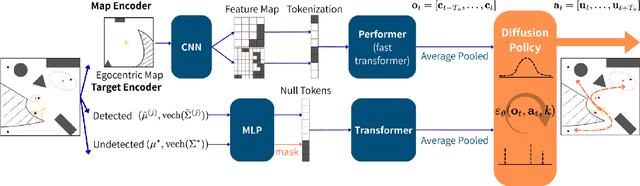
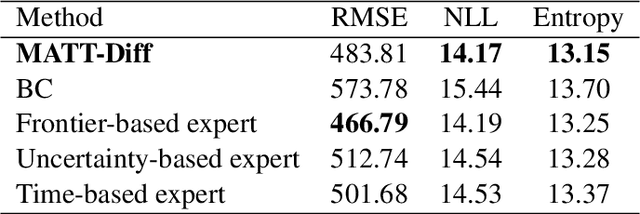
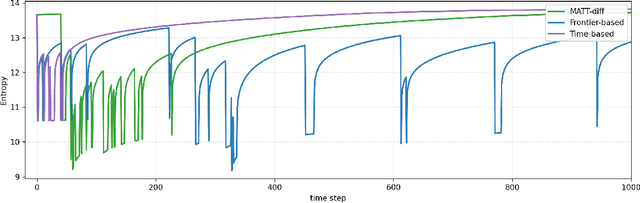
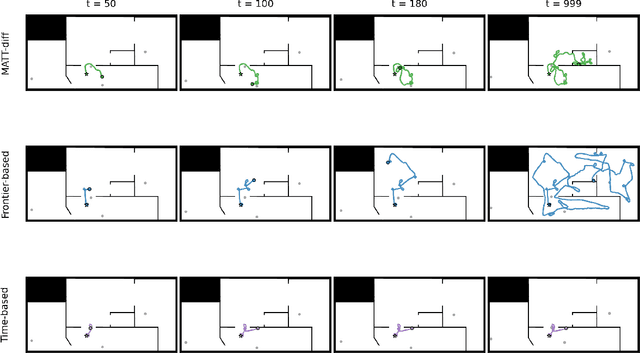
This paper proposes MATT-Diff: Multi-Modal Active Target Tracking by Diffusion Policy, a control policy that captures multiple behavioral modes - exploration, dedicated tracking, and target reacquisition - for active multi-target tracking. The policy enables agent control without prior knowledge of target numbers, states, or dynamics. Effective target tracking demands balancing exploration for undetected or lost targets with following the motion of detected but uncertain ones. We generate a demonstration dataset from three expert planners including frontier-based exploration, an uncertainty-based hybrid planner switching between frontier-based exploration and RRT* tracking based on target uncertainty, and a time-based hybrid planner switching between exploration and tracking based on target detection time. We design a control policy utilizing a vision transformer for egocentric map tokenization and an attention mechanism to integrate variable target estimates represented by Gaussian densities. Trained as a diffusion model, the policy learns to generate multi-modal action sequences through a denoising process. Evaluations demonstrate MATT-Diff's superior tracking performance against expert and behavior cloning baselines across multiple target motions, empirically validating its advantages in target tracking.

A Shared-Autonomy Construction Robotic System for Overhead Works

We present the ongoing development of a robotic system for overhead work such as ceiling drilling. The hardware platform comprises a mobile base with a two-stage lift, on which a bimanual torso is mounted with a custom-designed drilling end effector and RGB-D cameras. To support teleoperation in dynamic environments with limited visibility, we use Gaussian splatting for online 3D reconstruction and introduce motion parameters to model moving objects. For safe operation around dynamic obstacles, we developed a neural configuration-space barrier approach for planning and control. Initial feasibility studies demonstrate the capability of the hardware in drilling, bolting, and anchoring, and the software in safe teleoperation in a dynamic environment.

$ abla$-SDF: Learning Euclidean Signed Distance Functions Online with Gradient-Augmented Octree Interpolation and Neural Residual

Estimation of signed distance functions (SDFs) from point cloud data has been shown to benefit many robot autonomy capabilities, including localization, mapping, motion planning, and control. Methods that support online and large-scale SDF reconstruction tend to rely on discrete volumetric data structures, which affect the continuity and differentiability of the SDF estimates. Recently, using implicit features, neural network methods have demonstrated high-fidelity and differentiable SDF reconstruction but they tend to be less efficient, can experience catastrophic forgetting and memory limitations in large environments, and are often restricted to truncated SDFs. This work proposes $\nabla$-SDF, a hybrid method that combines an explicit prior obtained from gradient-augmented octree interpolation with an implicit neural residual. Our method achieves non-truncated (Euclidean) SDF reconstruction with computational and memory efficiency comparable to volumetric methods and differentiability and accuracy comparable to neural network methods. Extensive experiments demonstrate that \methodname{} outperforms the state of the art in terms of accuracy and efficiency, providing a scalable solution for downstream tasks in robotics and computer vision.

Certifying Stability of Reinforcement Learning Policies using Generalized Lyapunov Functions

We study the problem of certifying the stability of closed-loop systems under control policies derived from optimal control or reinforcement learning (RL). Classical Lyapunov methods require a strict step-wise decrease in the Lyapunov function but such a certificate is difficult to construct for a learned control policy. The value function associated with an RL policy is a natural Lyapunov function candidate but it is not clear how it should be modified. To gain intuition, we first study the linear quadratic regulator (LQR) problem and make two key observations. First, a Lyapunov function can be obtained from the value function of an LQR policy by augmenting it with a residual term related to the system dynamics and stage cost. Second, the classical Lyapunov decrease requirement can be relaxed to a generalized Lyapunov condition requiring only decrease on average over multiple time steps. Using this intuition, we consider the nonlinear setting and formulate an approach to learn generalized Lyapunov functions by augmenting RL value functions with neural network residual terms. Our approach successfully certifies the stability of RL policies trained on Gymnasium and DeepMind Control benchmarks. We also extend our method to jointly train neural controllers and stability certificates using a multi-step Lyapunov loss, resulting in larger certified inner approximations of the region of attraction compared to the classical Lyapunov approach. Overall, our formulation enables stability certification for a broad class of systems with learned policies by making certificates easier to construct, thereby bridging classical control theory and modern learning-based methods.

Learned IMU Bias Prediction for Invariant Visual Inertial Odometry

Autonomous mobile robots operating in novel environments depend critically on accurate state estimation, often utilizing visual and inertial measurements. Recent work has shown that an invariant formulation of the extended Kalman filter improves the convergence and robustness of visual-inertial odometry by utilizing the Lie group structure of a robot's position, velocity, and orientation states. However, inertial sensors also require measurement bias estimation, yet introducing the bias in the filter state breaks the Lie group symmetry. In this paper, we design a neural network to predict the bias of an inertial measurement unit (IMU) from a sequence of previous IMU measurements. This allows us to use an invariant filter for visual inertial odometry, relying on the learned bias prediction rather than introducing the bias in the filter state. We demonstrate that an invariant multi-state constraint Kalman filter (MSCKF) with learned bias predictions achieves robust visual-inertial odometry in real experiments, even when visual information is unavailable for extended periods and the system needs to rely solely on IMU measurements.

Variational Formulation of the Particle Flow Particle Filter

This paper provides a formulation of the particle flow particle filter from the perspective of variational inference. We show that the transient density used to derive the particle flow particle filter follows a time-scaled trajectory of the Fisher-Rao gradient flow in the space of probability densities. The Fisher-Rao gradient flow is obtained as a continuous-time algorithm for variational inference, minimizing the Kullback-Leibler divergence between a variational density and the true posterior density.

MISO: Multiresolution Submap Optimization for Efficient Globally Consistent Neural Implicit Reconstruction

Neural implicit representations have had a significant impact on simultaneous localization and mapping (SLAM) by enabling robots to build continuous, differentiable, and high-fidelity 3D maps from sensor data. However, as the scale and complexity of the environment increase, neural SLAM approaches face renewed challenges in the back-end optimization process to keep up with runtime requirements and maintain global consistency. We introduce MISO, a hierarchical optimization approach that leverages multiresolution submaps to achieve efficient and scalable neural implicit reconstruction. For local SLAM within each submap, we develop a hierarchical optimization scheme with learned initialization that substantially reduces the time needed to optimize the implicit submap features. To correct estimation drift globally, we develop a hierarchical method to align and fuse the multiresolution submaps, leading to substantial acceleration by avoiding the need to decode the full scene geometry. MISO significantly improves computational efficiency and estimation accuracy of neural signed distance function (SDF) SLAM on large-scale real-world benchmarks.

Learning Scene-Level Signed Directional Distance Function with Ellipsoidal Priors and Neural Residuals

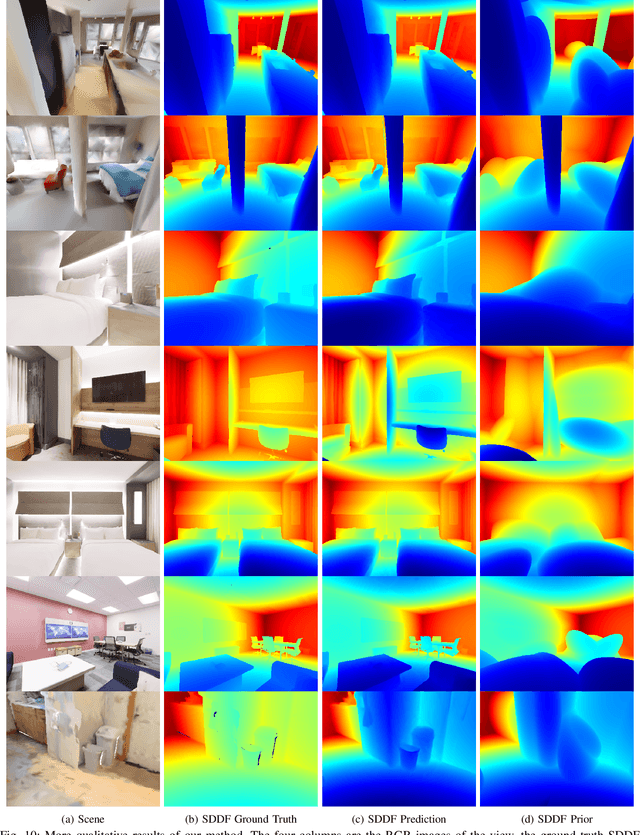
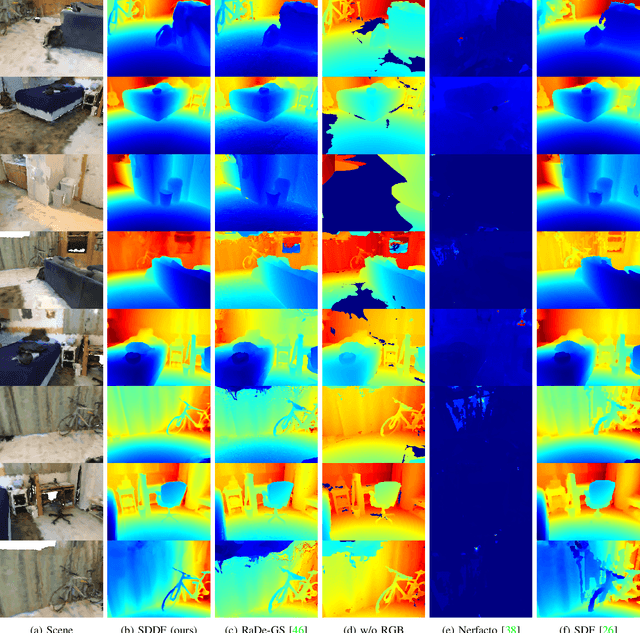
Dense geometric environment representations are critical for autonomous mobile robot navigation and exploration. Recent work shows that implicit continuous representations of occupancy, signed distance, or radiance learned using neural networks offer advantages in reconstruction fidelity, efficiency, and differentiability over explicit discrete representations based on meshes, point clouds, and voxels. In this work, we explore a directional formulation of signed distance, called signed directional distance function (SDDF). Unlike signed distance function (SDF) and similar to neural radiance fields (NeRF), SDDF has a position and viewing direction as input. Like SDF and unlike NeRF, SDDF directly provides distance to the observed surface along the direction, rather than integrating along the view ray, allowing efficient view synthesis. To learn and predict scene-level SDDF efficiently, we develop a differentiable hybrid representation that combines explicit ellipsoid priors and implicit neural residuals. This approach allows the model to effectively handle large distance discontinuities around obstacle boundaries while preserving the ability for dense high-fidelity prediction. We show that SDDF is competitive with the state-of-the-art neural implicit scene models in terms of reconstruction accuracy and rendering efficiency, while allowing differentiable view prediction for robot trajectory optimization.

DynaGSLAM: Real-Time Gaussian-Splatting SLAM for Online Rendering, Tracking, Motion Predictions of Moving Objects in Dynamic Scenes

Simultaneous Localization and Mapping (SLAM) is one of the most important environment-perception and navigation algorithms for computer vision, robotics, and autonomous cars/drones. Hence, high quality and fast mapping becomes a fundamental problem. With the advent of 3D Gaussian Splatting (3DGS) as an explicit representation with excellent rendering quality and speed, state-of-the-art (SOTA) works introduce GS to SLAM. Compared to classical pointcloud-SLAM, GS-SLAM generates photometric information by learning from input camera views and synthesize unseen views with high-quality textures. However, these GS-SLAM fail when moving objects occupy the scene that violate the static assumption of bundle adjustment. The failed updates of moving GS affects the static GS and contaminates the full map over long frames. Although some efforts have been made by concurrent works to consider moving objects for GS-SLAM, they simply detect and remove the moving regions from GS rendering ("anti'' dynamic GS-SLAM), where only the static background could benefit from GS. To this end, we propose the first real-time GS-SLAM, "DynaGSLAM'', that achieves high-quality online GS rendering, tracking, motion predictions of moving objects in dynamic scenes while jointly estimating accurate ego motion. Our DynaGSLAM outperforms SOTA static & "Anti'' dynamic GS-SLAM on three dynamic real datasets, while keeping speed and memory efficiency in practice.

LATMOS: Latent Automaton Task Model from Observation Sequences

Robot task planning from high-level instructions is an important step towards deploying fully autonomous robot systems in the service sector. Three key aspects of robot task planning present challenges yet to be resolved simultaneously, namely, (i) factorization of complex tasks specifications into simpler executable subtasks, (ii) understanding of the current task state from raw observations, and (iii) planning and verification of task executions. To address these challenges, we propose LATMOS, an automata-inspired task model that, given observations from correct task executions, is able to factorize the task, while supporting verification and planning operations. LATMOS combines an observation encoder to extract the features from potentially high-dimensional observations with automata theory to learn a sequential model that encapsulates an automaton with symbols in the latent feature space. We conduct extensive evaluations in three task model learning setups: (i) abstract tasks described by logical formulas, (ii) real-world human tasks described by videos and natural language prompts and (iii) a robot task described by image and state observations. The results demonstrate the improved plan generation and verification capabilities of LATMOS across observation modalities and tasks.