Spuriosity Didn't Kill the Classifier: Using Invariant Predictions to Harness Spurious Features

To avoid failures on out-of-distribution data, recent works have sought to extract features that have a stable or invariant relationship with the label across domains, discarding the "spurious" or unstable features whose relationship with the label changes across domains. However, unstable features often carry complementary information about the label that could boost performance if used correctly in the test domain. Our main contribution is to show that it is possible to learn how to use these unstable features in the test domain without labels. In particular, we prove that pseudo-labels based on stable features provide sufficient guidance for doing so, provided that stable and unstable features are conditionally independent given the label. Based on this theoretical insight, we propose Stable Feature Boosting (SFB), an algorithm for: (i) learning a predictor that separates stable and conditionally-independent unstable features; and (ii) using the stable-feature predictions to adapt the unstable-feature predictions in the test domain. Theoretically, we prove that SFB can learn an asymptotically-optimal predictor without test-domain labels. Empirically, we demonstrate the effectiveness of SFB on real and synthetic data.

Decoding Attention from Gaze: A Benchmark Dataset and End-to-End Models

Eye-tracking has potential to provide rich behavioral data about human cognition in ecologically valid environments. However, analyzing this rich data is often challenging. Most automated analyses are specific to simplistic artificial visual stimuli with well-separated, static regions of interest, while most analyses in the context of complex visual stimuli, such as most natural scenes, rely on laborious and time-consuming manual annotation. This paper studies using computer vision tools for "attention decoding", the task of assessing the locus of a participant's overt visual attention over time. We provide a publicly available Multiple Object Eye-Tracking (MOET) dataset, consisting of gaze data from participants tracking specific objects, annotated with labels and bounding boxes, in crowded real-world videos, for training and evaluating attention decoding algorithms. We also propose two end-to-end deep learning models for attention decoding and compare these to state-of-the-art heuristic methods.

Probable Domain Generalization via Quantile Risk Minimization

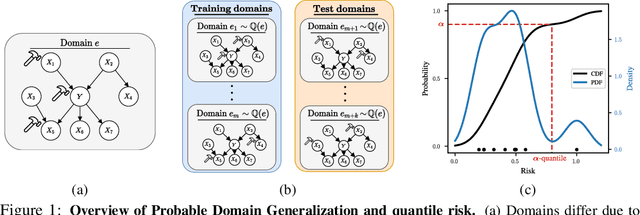
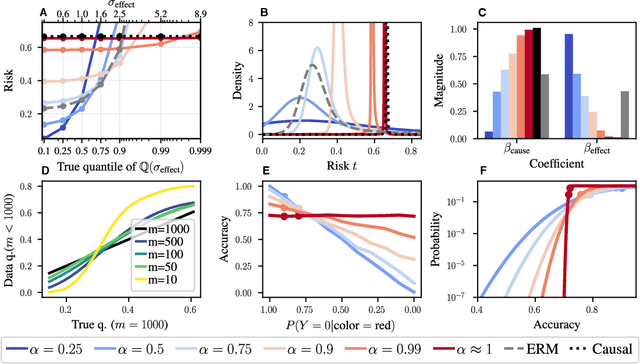
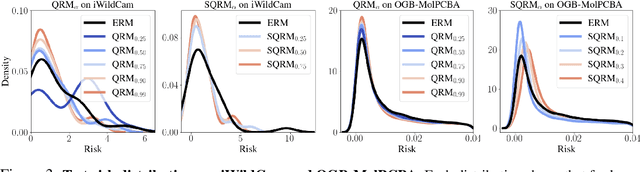
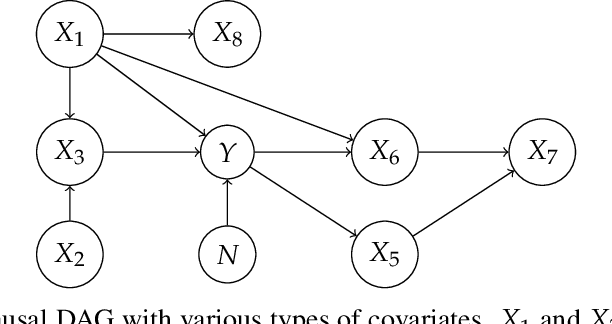
Domain generalization (DG) seeks predictors which perform well on unseen test distributions by leveraging labeled training data from multiple related distributions or domains. To achieve this, the standard formulation optimizes for worst-case performance over the set of all possible domains. However, with worst-case shifts very unlikely in practice, this generally leads to overly-conservative solutions. In fact, a recent study found that no DG algorithm outperformed empirical risk minimization in terms of average performance. In this work, we argue that DG is neither a worst-case problem nor an average-case problem, but rather a probabilistic one. To this end, we propose a probabilistic framework for DG, which we call Probable Domain Generalization, wherein our key idea is that distribution shifts seen during training should inform us of probable shifts at test time. To realize this, we explicitly relate training and test domains as draws from the same underlying meta-distribution, and propose a new optimization problem -- Quantile Risk Minimization (QRM) -- which requires that predictors generalize with high probability. We then prove that QRM: (i) produces predictors that generalize to new domains with a desired probability, given sufficiently many domains and samples; and (ii) recovers the causal predictor as the desired probability of generalization approaches one. In our experiments, we introduce a more holistic quantile-focused evaluation protocol for DG, and show that our algorithms outperform state-of-the-art baselines on real and synthetic data.

Indirect Active Learning

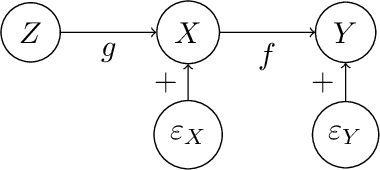
Traditional models of active learning assume a learner can directly manipulate or query a covariate $X$ in order to study its relationship with a response $Y$. However, if $X$ is a feature of a complex system, it may be possible only to indirectly influence $X$ by manipulating a control variable $Z$, a scenario we refer to as Indirect Active Learning. Under a nonparametric model of Indirect Active Learning with a fixed budget, we study minimax convergence rates for estimating the relationship between $X$ and $Y$ locally at a point, obtaining different rates depending on the complexities and noise levels of the relationships between $Z$ and $X$ and between $X$ and $Y$. We also identify minimax rates for passive learning under comparable assumptions. In many cases, our results show that, while there is an asymptotic benefit to active learning, this benefit is fully realized by a simple two-stage learner that runs two passive experiments in sequence.

Statistical Theory for Imbalanced Binary Classification

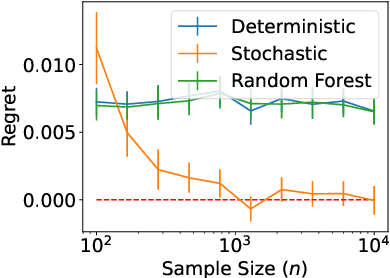
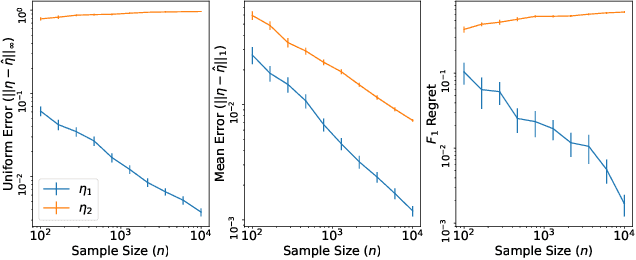
Within the vast body of statistical theory developed for binary classification, few meaningful results exist for imbalanced classification, in which data are dominated by samples from one of the two classes. Existing theory faces at least two main challenges. First, meaningful results must consider more complex performance measures than classification accuracy. To address this, we characterize a novel generalization of the Bayes-optimal classifier to any performance metric computed from the confusion matrix, and we use this to show how relative performance guarantees can be obtained in terms of the error of estimating the class probability function under uniform ($\mathcal{L}_\infty$) loss. Second, as we show, optimal classification performance depends on certain properties of class imbalance that have not previously been formalized. Specifically, we propose a novel sub-type of class imbalance, which we call Uniform Class Imbalance. We analyze how Uniform Class Imbalance influences optimal classifier performance and show that it necessitates different classifier behavior than other types of class imbalance. We further illustrate these two contributions in the case of $k$-nearest neighbor classification, for which we develop novel guarantees. Together, these results provide some of the first meaningful finite-sample statistical theory for imbalanced binary classification.

Continuum-Armed Bandits: A Function Space Perspective

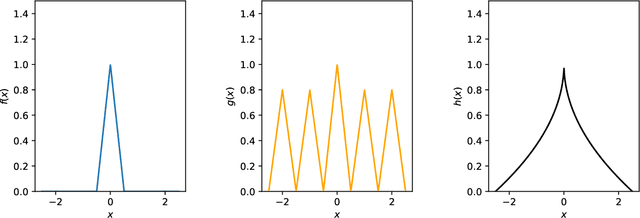
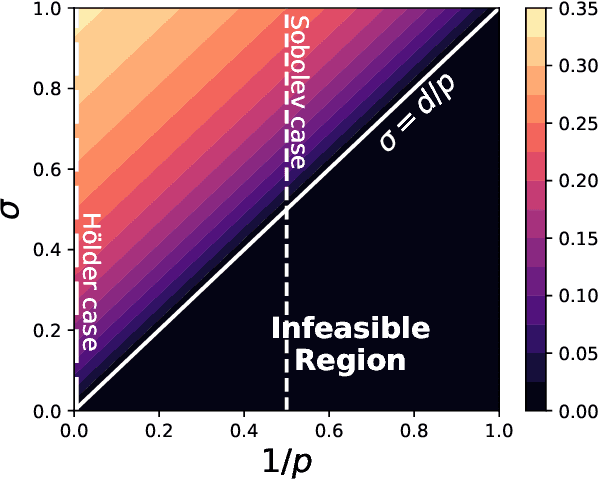
Continuum-armed bandits (a.k.a., black-box or $0^{th}$-order optimization) involves optimizing an unknown objective function given an oracle that evaluates the function at a query point, with the goal of using as few query points as possible. In the most well-studied case, the objective function is assumed to be Lipschitz continuous and minimax rates of simple and cumulative regrets are known in both noiseless and noisy settings. This paper studies continuum-armed bandits under more general smoothness conditions, namely Besov smoothness conditions, on the objective function. In both noiseless and noisy conditions, we derive minimax rates under simple and cumulative regrets. Our results show that minimax rates over objective functions in a Besov space are identical to minimax rates over objective functions in the smallest H\"older space into which the Besov space embeds.

Interpretable Sequence Learning for COVID-19 Forecasting

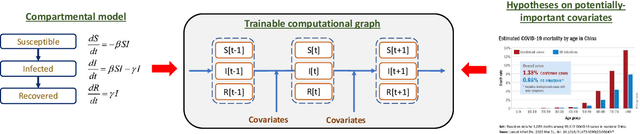
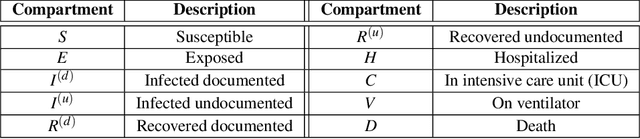
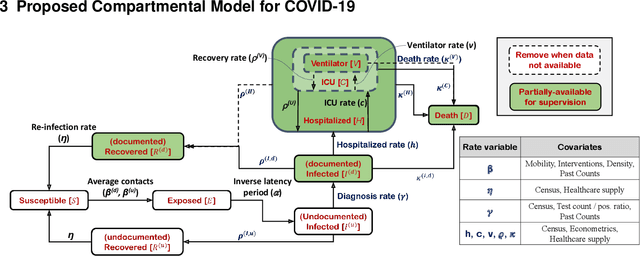
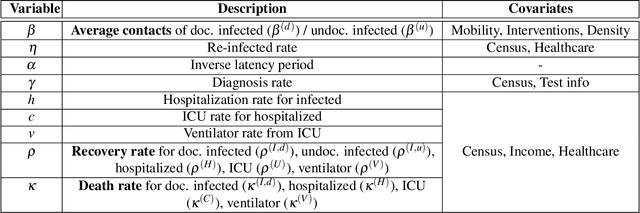
We propose a novel approach that integrates machine learning into compartmental disease modeling to predict the progression of COVID-19. Our model is explainable by design as it explicitly shows how different compartments evolve and it uses interpretable encoders to incorporate covariates and improve performance. Explainability is valuable to ensure that the model's forecasts are credible to epidemiologists and to instill confidence in end-users such as policy makers and healthcare institutions. Our model can be applied at different geographic resolutions, and here we demonstrate it for states and counties in the United States. We show that our model provides more accurate forecasts, in metrics averaged across the entire US, than state-of-the-art alternatives, and that it provides qualitatively meaningful explanatory insights. Lastly, we analyze the performance of our model for different subgroups based on the subgroup distributions within the counties.

Multiclass Classification via Class-Weighted Nearest Neighbors

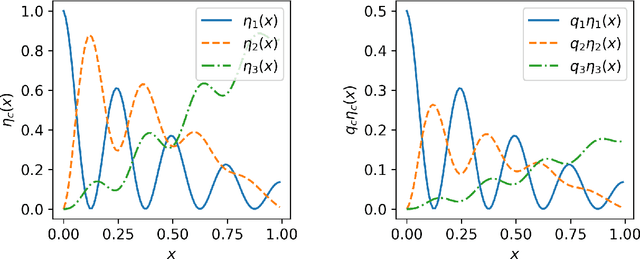
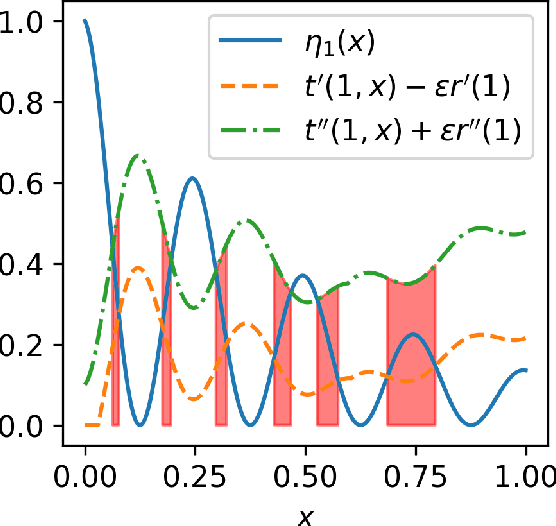
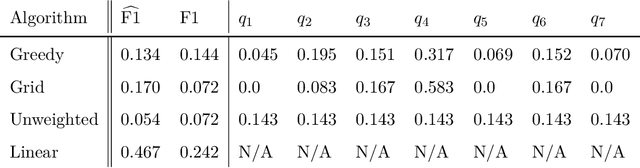
We study statistical properties of the k-nearest neighbors algorithm for multiclass classification, with a focus on settings where the number of classes may be large and/or classes may be highly imbalanced. In particular, we consider a variant of the k-nearest neighbor classifier with non-uniform class-weightings, for which we derive upper and minimax lower bounds on accuracy, class-weighted risk, and uniform error. Additionally, we show that uniform error bounds lead to bounds on the difference between empirical confusion matrix quantities and their population counterparts across a set of weights. As a result, we may adjust the class weights to optimize classification metrics such as F1 score or Matthew's Correlation Coefficient that are commonly used in practice, particularly in settings with imbalanced classes. We additionally provide a simple example to instantiate our bounds and numerical experiments.

Robust Density Estimation under Besov IPM Losses

We study minimax convergence rates of nonparametric density estimation in the Huber contamination model, in which a proportion of the data comes from an unknown outlier distribution. We provide the first results for this problem under a large family of losses, called Besov integral probability metrics (IPMs), that includes $\mathcal{L}^p$, Wasserstein, Kolmogorov-Smirnov, and other common distances between probability distributions. Specifically, under a range of smoothness assumptions on the population and outlier distributions, we show that a re-scaled thresholding wavelet series estimator achieves minimax optimal convergence rates under a wide variety of losses. Finally, based on connections that have recently been shown between nonparametric density estimation under IPM losses and generative adversarial networks (GANs), we show that certain GAN architectures also achieve these minimax rates.

DARC: Differentiable ARchitecture Compression

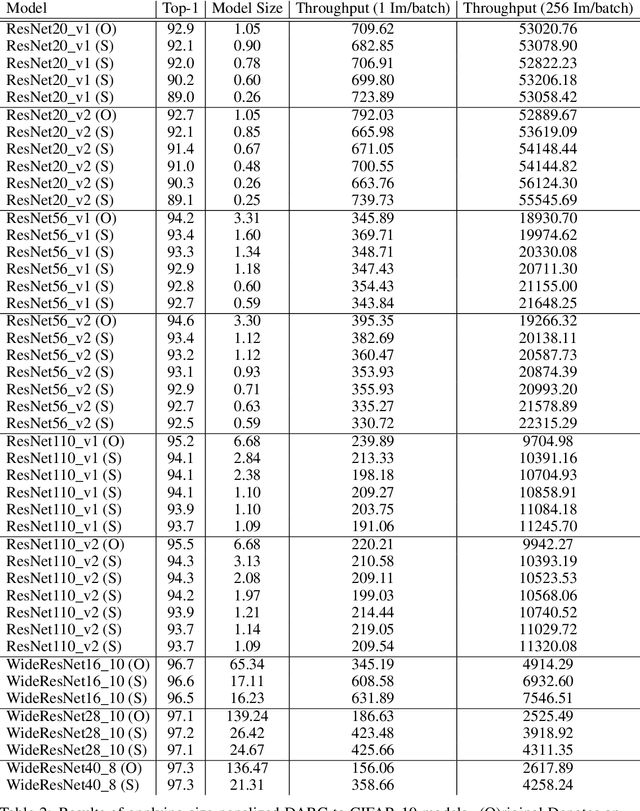
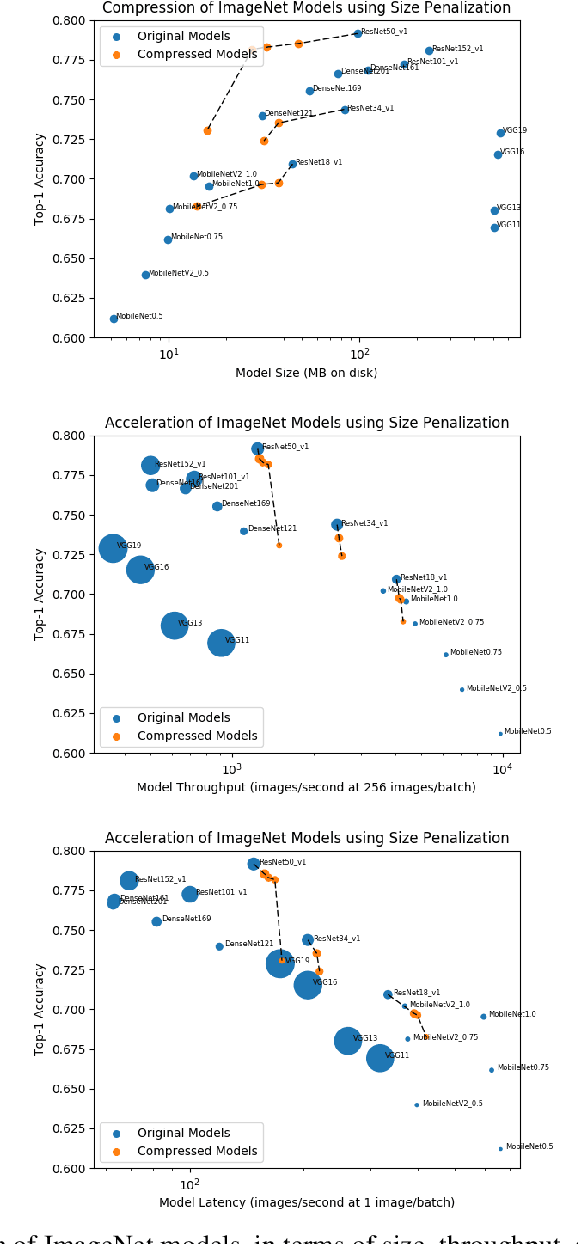
In many learning situations, resources at inference time are significantly more constrained than resources at training time. This paper studies a general paradigm, called Differentiable ARchitecture Compression (DARC), that combines model compression and architecture search to learn models that are resource-efficient at inference time. Given a resource-intensive base architecture, DARC utilizes the training data to learn which sub-components can be replaced by cheaper alternatives. The high-level technique can be applied to any neural architecture, and we report experiments on state-of-the-art convolutional neural networks for image classification. For a WideResNet with $97.2\%$ accuracy on CIFAR-10, we improve single-sample inference speed by $2.28\times$ and memory footprint by $5.64\times$, with no accuracy loss. For a ResNet with $79.15\%$ Top1 accuracy on ImageNet, we improve batch inference speed by $1.29\times$ and memory footprint by $3.57\times$ with $1\%$ accuracy loss. We also give theoretical Rademacher complexity bounds in simplified cases, showing how DARC avoids overfitting despite over-parameterization.