Uncertainty-Calibrated Prediction of Randomly-Timed Biomarker Trajectories with Conformal Bands

Despite recent progress in predicting biomarker trajectories from real clinical data, uncertainty in the predictions poses high-stakes risks (e.g., misdiagnosis) that limit their clinical deployment. To enable safe and reliable use of such predictions in healthcare, we introduce a conformal method for uncertainty-calibrated prediction of biomarker trajectories resulting from randomly-timed clinical visits of patients. Our approach extends conformal prediction to the setting of randomly-timed trajectories via a novel nonconformity score that produces prediction bands guaranteed to cover the unknown biomarker trajectories with a user-prescribed probability. We apply our method across a wide range of standard and state-of-the-art predictors for two well-established brain biomarkers of Alzheimer's disease, using neuroimaging data from real clinical studies. We observe that our conformal prediction bands consistently achieve the desired coverage, while also being tighter than baseline prediction bands. To further account for population heterogeneity, we develop group-conditional conformal bands and test their coverage guarantees across various demographic and clinically relevant subpopulations. Moreover, we demonstrate the clinical utility of our conformal bands in identifying subjects at high risk of progression to Alzheimer's disease. Specifically, we introduce an uncertainty-calibrated risk score that enables the identification of 17.5% more high-risk subjects compared to standard risk scores, highlighting the value of uncertainty calibration in real-world clinical decision making. Our code is available at github.com/vatass/ConformalBiomarkerTrajectories.

Recursively Feasible Shrinking-Horizon MPC in Dynamic Environments with Conformal Prediction Guarantees

In this paper, we focus on the problem of shrinking-horizon Model Predictive Control (MPC) in uncertain dynamic environments. We consider controlling a deterministic autonomous system that interacts with uncontrollable stochastic agents during its mission. Employing tools from conformal prediction, existing works derive high-confidence prediction regions for the unknown agent trajectories, and integrate these regions in the design of suitable safety constraints for MPC. Despite guaranteeing probabilistic safety of the closed-loop trajectories, these constraints do not ensure feasibility of the respective MPC schemes for the entire duration of the mission. We propose a shrinking-horizon MPC that guarantees recursive feasibility via a gradual relaxation of the safety constraints as new prediction regions become available online. This relaxation enforces the safety constraints to hold over the least restrictive prediction region from the set of all available prediction regions. In a comparative case study with the state of the art, we empirically show that our approach results in tighter prediction regions and verify recursive feasibility of our MPC scheme.

Rate-Optimal Non-Asymptotics for the Quadratic Prediction Error Method

We study the quadratic prediction error method -- i.e., nonlinear least squares -- for a class of time-varying parametric predictor models satisfying a certain identifiability condition. While this method is known to asymptotically achieve the optimal rate for a wide range of problems, there have been no non-asymptotic results matching these optimal rates outside of a select few, typically linear, model classes. By leveraging modern tools from learning with dependent data, we provide the first rate-optimal non-asymptotic analysis of this method for our more general setting of nonlinearly parametrized model classes. Moreover, we show that our results can be applied to a particular class of identifiable AutoRegressive Moving Average (ARMA) models, resulting in the first optimal non-asymptotic rates for identification of ARMA models.

Adaptive Stochastic MPC under Unknown Noise Distribution

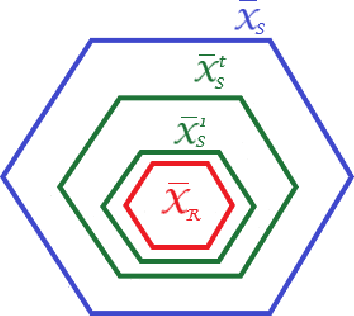
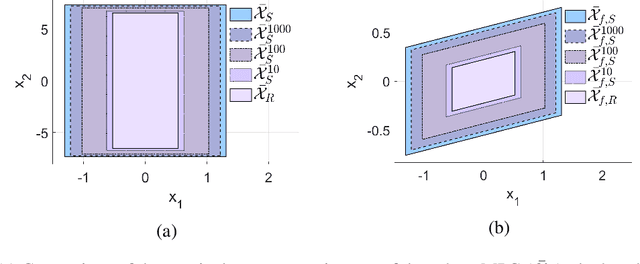
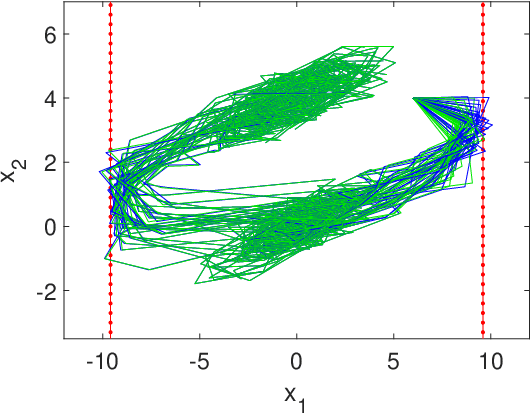
In this paper, we address the stochastic MPC (SMPC) problem for linear systems, subject to chance state constraints and hard input constraints, under unknown noise distribution. First, we reformulate the chance state constraints as deterministic constraints depending only on explicit noise statistics. Based on these reformulated constraints, we design a distributionally robust and robustly stable benchmark SMPC algorithm for the ideal setting of known noise statistics. Then, we employ this benchmark controller to derive a novel robustly stable adaptive SMPC scheme that learns the necessary noise statistics online, while guaranteeing time-uniform satisfaction of the unknown reformulated state constraints with high probability. The latter is achieved through the use of confidence intervals which rely on the empirical noise statistics and are valid uniformly over time. Moreover, control performance is improved over time as more noise samples are gathered and better estimates of the noise statistics are obtained, given the online adaptation of the estimated reformulated constraints. Additionally, in tracking problems with multiple successive targets our approach leads to an online-enlarged domain of attraction compared to robust tube-based MPC. A numerical simulation of a DC-DC converter is used to demonstrate the effectiveness of the developed methodology.