Online Residual Learning from Offline Experts for Pedestrian Tracking

In this paper, we consider the problem of predicting unknown targets from data. We propose Online Residual Learning (ORL), a method that combines online adaptation with offline-trained predictions. At a lower level, we employ multiple offline predictions generated before or at the beginning of the prediction horizon. We augment every offline prediction by learning their respective residual error concerning the true target state online, using the recursive least squares algorithm. At a higher level, we treat the augmented lower-level predictors as experts, adopting the Prediction with Expert Advice framework. We utilize an adaptive softmax weighting scheme to form an aggregate prediction and provide guarantees for ORL in terms of regret. We employ ORL to boost performance in the setting of online pedestrian trajectory prediction. Based on data from the Stanford Drone Dataset, we show that ORL can demonstrate best-of-both-worlds performance.

Finite Sample Frequency Domain Identification

We study non-parametric frequency-domain system identification from a finite-sample perspective. We assume an open loop scenario where the excitation input is periodic and consider the Empirical Transfer Function Estimate (ETFE), where the goal is to estimate the frequency response at certain desired (evenly-spaced) frequencies, given input-output samples. We show that under sub-Gaussian colored noise (in time-domain) and stability assumptions, the ETFE estimates are concentrated around the true values. The error rate is of the order of $\mathcal{O}((d_{\mathrm{u}}+\sqrt{d_{\mathrm{u}}d_{\mathrm{y}}})\sqrt{M/N_{\mathrm{tot}}})$, where $N_{\mathrm{tot}}$ is the total number of samples, $M$ is the number of desired frequencies, and $d_{\mathrm{u}},\,d_{\mathrm{y}}$ are the dimensions of the input and output signals respectively. This rate remains valid for general irrational transfer functions and does not require a finite order state-space representation. By tuning $M$, we obtain a $N_{\mathrm{tot}}^{-1/3}$ finite-sample rate for learning the frequency response over all frequencies in the $ \mathcal{H}_{\infty}$ norm. Our result draws upon an extension of the Hanson-Wright inequality to semi-infinite matrices. We study the finite-sample behavior of ETFE in simulations.

Predictive Linear Online Tracking for Unknown Targets

In this paper, we study the problem of online tracking in linear control systems, where the objective is to follow a moving target. Unlike classical tracking control, the target is unknown, non-stationary, and its state is revealed sequentially, thus, fitting the framework of online non-stochastic control. We consider the case of quadratic costs and propose a new algorithm, called predictive linear online tracking (PLOT). The algorithm uses recursive least squares with exponential forgetting to learn a time-varying dynamic model of the target. The learned model is used in the optimal policy under the framework of receding horizon control. We show the dynamic regret of PLOT scales with $\mathcal{O}(\sqrt{TV_T})$, where $V_T$ is the total variation of the target dynamics and $T$ is the time horizon. Unlike prior work, our theoretical results hold for non-stationary targets. We implement PLOT on a real quadrotor and provide open-source software, thus, showcasing one of the first successful applications of online control methods on real hardware.

A Tutorial on the Non-Asymptotic Theory of System Identification

This tutorial serves as an introduction to recently developed non-asymptotic methods in the theory of -- mainly linear -- system identification. We emphasize tools we deem particularly useful for a range of problems in this domain, such as the covering technique, the Hanson-Wright Inequality and the method of self-normalized martingales. We then employ these tools to give streamlined proofs of the performance of various least-squares based estimators for identifying the parameters in autoregressive models. We conclude by sketching out how the ideas presented herein can be extended to certain nonlinear identification problems.

Suboptimality analysis of receding horizon quadratic control with unknown linear systems and its applications in learning-based control

For a receding-horizon controller with a known system and with an approximate terminal value function, it is well-known that increasing the prediction horizon can improve its control performance. However, when the prediction model is inexact, a larger prediction horizon also causes propagation and accumulation of the prediction error. In this work, we aim to analyze the effect of the above trade-off between the modeling error, the terminal value function error, and the prediction horizon on the performance of a nominal receding-horizon linear quadratic (LQ) controller. By developing a novel perturbation result of the Riccati difference equation, a performance upper bound is obtained and suggests that for many cases, the prediction horizon should be either 1 or infinity to improve the control performance, depending on the relative difference between the modeling error and the terminal value function error. The obtained suboptimality performance bound is also applied to provide end-to-end performance guarantees, e.g., regret bounds, for nominal receding-horizon LQ controllers in a learning-based setting.

Implications of Regret on Stability of Linear Dynamical Systems

The setting of an agent making decisions under uncertainty and under dynamic constraints is common for the fields of optimal control, reinforcement learning and recently also for online learning. In the online learning setting, the quality of an agent's decision is often quantified by the concept of regret, comparing the performance of the chosen decisions to the best possible ones in hindsight. While regret is a useful performance measure, when dynamical systems are concerned, it is important to also assess the stability of the closed-loop system for a chosen policy. In this work, we show that for linear state feedback policies and linear systems subject to adversarial disturbances, linear regret implies asymptotic stability in both time-varying and time-invariant settings. Conversely, we also show that bounded input bounded state (BIBS) stability and summability of the state transition matrices imply linear regret.

Statistical Learning Theory for Control: A Finite Sample Perspective

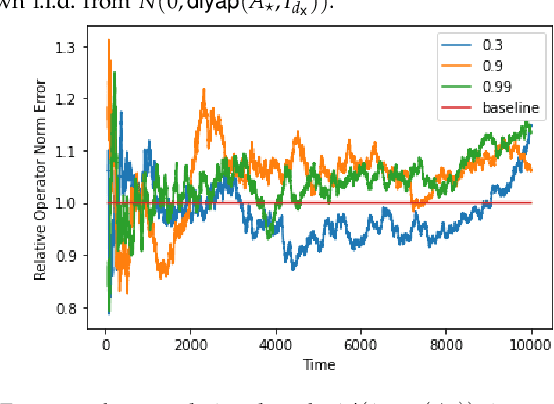
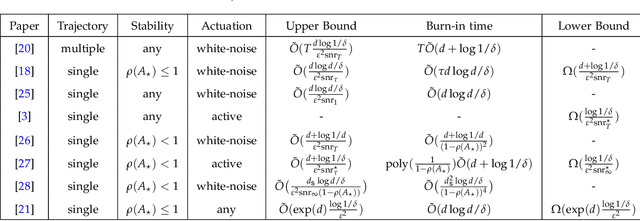
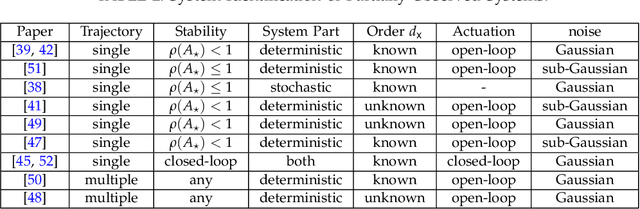
This tutorial survey provides an overview of recent non-asymptotic advances in statistical learning theory as relevant to control and system identification. While there has been substantial progress across all areas of control, the theory is most well-developed when it comes to linear system identification and learning for the linear quadratic regulator, which are the focus of this manuscript. From a theoretical perspective, much of the labor underlying these advances has been in adapting tools from modern high-dimensional statistics and learning theory. While highly relevant to control theorists interested in integrating tools from machine learning, the foundational material has not always been easily accessible. To remedy this, we provide a self-contained presentation of the relevant material, outlining all the key ideas and the technical machinery that underpin recent results. We also present a number of open problems and future directions.

How are policy gradient methods affected by the limits of control?

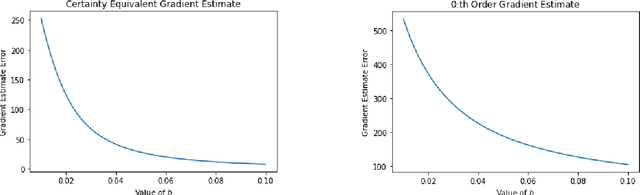
We study stochastic policy gradient methods from the perspective of control-theoretic limitations. Our main result is that ill-conditioned linear systems in the sense of Doyle inevitably lead to noisy gradient estimates. We also give an example of a class of stable systems in which policy gradient methods suffer from the curse of dimensionality. Our results apply to both state feedback and partially observed systems.

Learning to Control Linear Systems can be Hard

In this paper, we study the statistical difficulty of learning to control linear systems. We focus on two standard benchmarks, the sample complexity of stabilization, and the regret of the online learning of the Linear Quadratic Regulator (LQR). Prior results state that the statistical difficulty for both benchmarks scales polynomially with the system state dimension up to system-theoretic quantities. However, this does not reveal the whole picture. By utilizing minimax lower bounds for both benchmarks, we prove that there exist non-trivial classes of systems for which learning complexity scales dramatically, i.e. exponentially, with the system dimension. This situation arises in the case of underactuated systems, i.e. systems with fewer inputs than states. Such systems are structurally difficult to control and their system theoretic quantities can scale exponentially with the system dimension dominating learning complexity. Under some additional structural assumptions (bounding systems away from uncontrollability), we provide qualitatively matching upper bounds. We prove that learning complexity can be at most exponential with the controllability index of the system, that is the degree of underactuation.

Adaptive Stochastic MPC under Unknown Noise Distribution

In this paper, we address the stochastic MPC (SMPC) problem for linear systems, subject to chance state constraints and hard input constraints, under unknown noise distribution. First, we reformulate the chance state constraints as deterministic constraints depending only on explicit noise statistics. Based on these reformulated constraints, we design a distributionally robust and robustly stable benchmark SMPC algorithm for the ideal setting of known noise statistics. Then, we employ this benchmark controller to derive a novel robustly stable adaptive SMPC scheme that learns the necessary noise statistics online, while guaranteeing time-uniform satisfaction of the unknown reformulated state constraints with high probability. The latter is achieved through the use of confidence intervals which rely on the empirical noise statistics and are valid uniformly over time. Moreover, control performance is improved over time as more noise samples are gathered and better estimates of the noise statistics are obtained, given the online adaptation of the estimated reformulated constraints. Additionally, in tracking problems with multiple successive targets our approach leads to an online-enlarged domain of attraction compared to robust tube-based MPC. A numerical simulation of a DC-DC converter is used to demonstrate the effectiveness of the developed methodology.