Obfuscated Activations Bypass LLM Latent-Space Defenses

Recent latent-space monitoring techniques have shown promise as defenses against LLM attacks. These defenses act as scanners that seek to detect harmful activations before they lead to undesirable actions. This prompts the question: Can models execute harmful behavior via inconspicuous latent states? Here, we study such obfuscated activations. We show that state-of-the-art latent-space defenses -- including sparse autoencoders, representation probing, and latent OOD detection -- are all vulnerable to obfuscated activations. For example, against probes trained to classify harmfulness, our attacks can often reduce recall from 100% to 0% while retaining a 90% jailbreaking rate. However, obfuscation has limits: we find that on a complex task (writing SQL code), obfuscation reduces model performance. Together, our results demonstrate that neural activations are highly malleable: we can reshape activation patterns in a variety of ways, often while preserving a network's behavior. This poses a fundamental challenge to latent-space defenses.

Evidence of Learned Look-Ahead in a Chess-Playing Neural Network

Do neural networks learn to implement algorithms such as look-ahead or search "in the wild"? Or do they rely purely on collections of simple heuristics? We present evidence of learned look-ahead in the policy network of Leela Chess Zero, the currently strongest neural chess engine. We find that Leela internally represents future optimal moves and that these representations are crucial for its final output in certain board states. Concretely, we exploit the fact that Leela is a transformer that treats every chessboard square like a token in language models, and give three lines of evidence (1) activations on certain squares of future moves are unusually important causally; (2) we find attention heads that move important information "forward and backward in time," e.g., from squares of future moves to squares of earlier ones; and (3) we train a simple probe that can predict the optimal move 2 turns ahead with 92% accuracy (in board states where Leela finds a single best line). These findings are an existence proof of learned look-ahead in neural networks and might be a step towards a better understanding of their capabilities.

Diffusion On Syntax Trees For Program Synthesis

Large language models generate code one token at a time. Their autoregressive generation process lacks the feedback of observing the program's output. Training LLMs to suggest edits directly can be challenging due to the scarcity of rich edit data. To address these problems, we propose neural diffusion models that operate on syntax trees of any context-free grammar. Similar to image diffusion models, our method also inverts ``noise'' applied to syntax trees. Rather than generating code sequentially, we iteratively edit it while preserving syntactic validity, which makes it easy to combine this neural model with search. We apply our approach to inverse graphics tasks, where our model learns to convert images into programs that produce those images. Combined with search, our model is able to write graphics programs, see the execution result, and debug them to meet the required specifications. We additionally show how our system can write graphics programs for hand-drawn sketches.

Foundational Challenges in Assuring Alignment and Safety of Large Language Models

This work identifies 18 foundational challenges in assuring the alignment and safety of large language models (LLMs). These challenges are organized into three different categories: scientific understanding of LLMs, development and deployment methods, and sociotechnical challenges. Based on the identified challenges, we pose $200+$ concrete research questions.

When Your AIs Deceive You: Challenges with Partial Observability of Human Evaluators in Reward Learning

Past analyses of reinforcement learning from human feedback (RLHF) assume that the human fully observes the environment. What happens when human feedback is based only on partial observations? We formally define two failure cases: deception and overjustification. Modeling the human as Boltzmann-rational w.r.t. a belief over trajectories, we prove conditions under which RLHF is guaranteed to result in policies that deceptively inflate their performance, overjustify their behavior to make an impression, or both. To help address these issues, we mathematically characterize how partial observability of the environment translates into (lack of) ambiguity in the learned return function. In some cases, accounting for partial observability makes it theoretically possible to recover the return function and thus the optimal policy, while in other cases, there is irreducible ambiguity. We caution against blindly applying RLHF in partially observable settings and propose research directions to help tackle these challenges.

STARC: A General Framework For Quantifying Differences Between Reward Functions

In order to solve a task using reinforcement learning, it is necessary to first formalise the goal of that task as a reward function. However, for many real-world tasks, it is very difficult to manually specify a reward function that never incentivises undesirable behaviour. As a result, it is increasingly popular to use reward learning algorithms, which attempt to learn a reward function from data. However, the theoretical foundations of reward learning are not yet well-developed. In particular, it is typically not known when a given reward learning algorithm with high probability will learn a reward function that is safe to optimise. This means that reward learning algorithms generally must be evaluated empirically, which is expensive, and that their failure modes are difficult to predict in advance. One of the roadblocks to deriving better theoretical guarantees is the lack of good methods for quantifying the difference between reward functions. In this paper we provide a solution to this problem, in the form of a class of pseudometrics on the space of all reward functions that we call STARC (STAndardised Reward Comparison) metrics. We show that STARC metrics induce both an upper and a lower bound on worst-case regret, which implies that our metrics are tight, and that any metric with the same properties must be bilipschitz equivalent to ours. Moreover, we also identify a number of issues with reward metrics proposed by earlier works. Finally, we evaluate our metrics empirically, to demonstrate their practical efficacy. STARC metrics can be used to make both theoretical and empirical analysis of reward learning algorithms both easier and more principled.

imitation: Clean Imitation Learning Implementations

imitation provides open-source implementations of imitation and reward learning algorithms in PyTorch. We include three inverse reinforcement learning (IRL) algorithms, three imitation learning algorithms and a preference comparison algorithm. The implementations have been benchmarked against previous results, and automated tests cover 98% of the code. Moreover, the algorithms are implemented in a modular fashion, making it simple to develop novel algorithms in the framework. Our source code, including documentation and examples, is available at https://github.com/HumanCompatibleAI/imitation

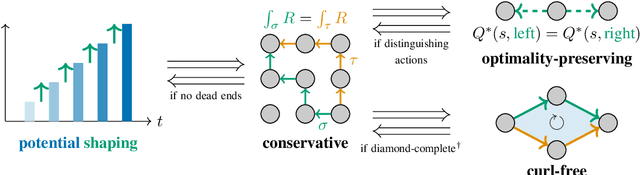
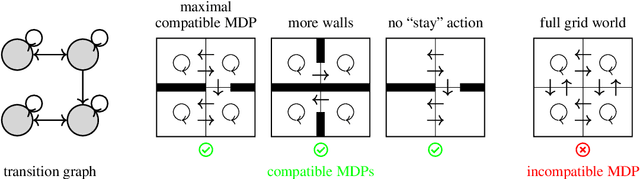
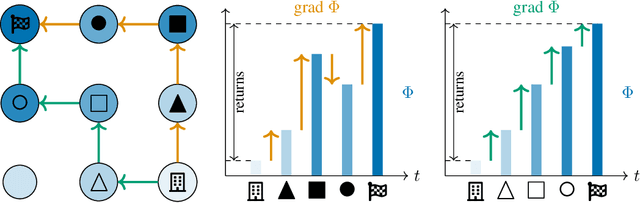
Calculus on MDPs: Potential Shaping as a Gradient

In reinforcement learning, different reward functions can be equivalent in terms of the optimal policies they induce. A particularly well-known and important example is potential shaping, a class of functions that can be added to any reward function without changing the optimal policy set under arbitrary transition dynamics. Potential shaping is conceptually similar to potentials, conservative vector fields and gauge transformations in math and physics, but this connection has not previously been formally explored. We develop a formalism for discrete calculus on graphs that abstract a Markov Decision Process, and show how potential shaping can be formally interpreted as a gradient within this framework. This allows us to strengthen results from Ng et al. (1999) describing conditions under which potential shaping is the only additive reward transformation to always preserve optimal policies. As an additional application of our formalism, we define a rule for picking a single unique reward function from each potential shaping equivalence class.

Preprocessing Reward Functions for Interpretability

In many real-world applications, the reward function is too complex to be manually specified. In such cases, reward functions must instead be learned from human feedback. Since the learned reward may fail to represent user preferences, it is important to be able to validate the learned reward function prior to deployment. One promising approach is to apply interpretability tools to the reward function to spot potential deviations from the user's intention. Existing work has applied general-purpose interpretability tools to understand learned reward functions. We propose exploiting the intrinsic structure of reward functions by first preprocessing them into simpler but equivalent reward functions, which are then visualized. We introduce a general framework for such reward preprocessing and propose concrete preprocessing algorithms. Our empirical evaluation shows that preprocessed rewards are often significantly easier to understand than the original reward.

Extensions of Karger's Algorithm: Why They Fail in Theory and How They Are Useful in Practice

The minimum graph cut and minimum $s$-$t$-cut problems are important primitives in the modeling of combinatorial problems in computer science, including in computer vision and machine learning. Some of the most efficient algorithms for finding global minimum cuts are randomized algorithms based on Karger's groundbreaking contraction algorithm. Here, we study whether Karger's algorithm can be successfully generalized to other cut problems. We first prove that a wide class of natural generalizations of Karger's algorithm cannot efficiently solve the $s$-$t$-mincut or the normalized cut problem to optimality. However, we then present a simple new algorithm for seeded segmentation / graph-based semi-supervised learning that is closely based on Karger's original algorithm, showing that for these problems, extensions of Karger's algorithm can be useful. The new algorithm has linear asymptotic runtime and yields a potential that can be interpreted as the posterior probability of a sample belonging to a given seed / class. We clarify its relation to the random walker algorithm / harmonic energy minimization in terms of distributions over spanning forests. On classical problems from seeded image segmentation and graph-based semi-supervised learning on image data, the method performs at least as well as the random walker / harmonic energy minimization / Gaussian processes.