Sample Complexity and Representation Ability of Test-time Scaling Paradigms

Test-time scaling paradigms have significantly advanced the capabilities of large language models (LLMs) on complex tasks. Despite their empirical success, theoretical understanding of the sample efficiency of various test-time strategies -- such as self-consistency, best-of-$n$, and self-correction -- remains limited. In this work, we first establish a separation result between two repeated sampling strategies: self-consistency requires $\Theta(1/\Delta^2)$ samples to produce the correct answer, while best-of-$n$ only needs $\Theta(1/\Delta)$, where $\Delta < 1$ denotes the probability gap between the correct and second most likely answers. Next, we present an expressiveness result for the self-correction approach with verifier feedback: it enables Transformers to simulate online learning over a pool of experts at test time. Therefore, a single Transformer architecture can provably solve multiple tasks without prior knowledge of the specific task associated with a user query, extending the representation theory of Transformers from single-task to multi-task settings. Finally, we empirically validate our theoretical results, demonstrating the practical effectiveness of self-correction methods.

Sounding that Object: Interactive Object-Aware Image to Audio Generation

Generating accurate sounds for complex audio-visual scenes is challenging, especially in the presence of multiple objects and sound sources. In this paper, we propose an {\em interactive object-aware audio generation} model that grounds sound generation in user-selected visual objects within images. Our method integrates object-centric learning into a conditional latent diffusion model, which learns to associate image regions with their corresponding sounds through multi-modal attention. At test time, our model employs image segmentation to allow users to interactively generate sounds at the {\em object} level. We theoretically validate that our attention mechanism functionally approximates test-time segmentation masks, ensuring the generated audio aligns with selected objects. Quantitative and qualitative evaluations show that our model outperforms baselines, achieving better alignment between objects and their associated sounds. Project page: https://tinglok.netlify.app/files/avobject/

Stochastic Zeroth-Order Optimization under Strongly Convexity and Lipschitz Hessian: Minimax Sample Complexity

Optimization of convex functions under stochastic zeroth-order feedback has been a major and challenging question in online learning. In this work, we consider the problem of optimizing second-order smooth and strongly convex functions where the algorithm is only accessible to noisy evaluations of the objective function it queries. We provide the first tight characterization for the rate of the minimax simple regret by developing matching upper and lower bounds. We propose an algorithm that features a combination of a bootstrapping stage and a mirror-descent stage. Our main technical innovation consists of a sharp characterization for the spherical-sampling gradient estimator under higher-order smoothness conditions, which allows the algorithm to optimally balance the bias-variance tradeoff, and a new iterative method for the bootstrapping stage, which maintains the performance for unbounded Hessian.

Data Acquisition via Experimental Design for Decentralized Data Markets

Acquiring high-quality training data is essential for current machine learning models. Data markets provide a way to increase the supply of data, particularly in data-scarce domains such as healthcare, by incentivizing potential data sellers to join the market. A major challenge for a data buyer in such a market is selecting the most valuable data points from a data seller. Unlike prior work in data valuation, which assumes centralized data access, we propose a federated approach to the data selection problem that is inspired by linear experimental design. Our proposed data selection method achieves lower prediction error without requiring labeled validation data and can be optimized in a fast and federated procedure. The key insight of our work is that a method that directly estimates the benefit of acquiring data for test set prediction is particularly compatible with a decentralized market setting.

Towards Optimal Statistical Watermarking

We study statistical watermarking by formulating it as a hypothesis testing problem, a general framework which subsumes all previous statistical watermarking methods. Key to our formulation is a coupling of the output tokens and the rejection region, realized by pseudo-random generators in practice, that allows non-trivial trade-off between the Type I error and Type II error. We characterize the Uniformly Most Powerful (UMP) watermark in this context. In the most common scenario where the output is a sequence of $n$ tokens, we establish matching upper and lower bounds on the number of i.i.d. tokens required to guarantee small Type I and Type II errors. Our rate scales as $\Theta(h^{-1} \log (1/h))$ with respect to the average entropy per token $h$ and thus greatly improves the $O(h^{-2})$ rate in the previous works. For scenarios where the detector lacks knowledge of the model's distribution, we introduce the concept of model-agnostic watermarking and establish the minimax bounds for the resultant increase in Type II error. Moreover, we formulate the robust watermarking problem where user is allowed to perform a class of perturbation on the generated texts, and characterize the optimal type II error of robust UMP tests via a linear programming problem. To the best of our knowledge, this is the first systematic statistical treatment on the watermarking problem with near-optimal rates in the i.i.d. setting, and might be of interest for future works.

On Representation Complexity of Model-based and Model-free Reinforcement Learning

We study the representation complexity of model-based and model-free reinforcement learning (RL) in the context of circuit complexity. We prove theoretically that there exists a broad class of MDPs such that their underlying transition and reward functions can be represented by constant depth circuits with polynomial size, while the optimal $Q$-function suffers an exponential circuit complexity in constant-depth circuits. By drawing attention to the approximation errors and building connections to complexity theory, our theory provides unique insights into why model-based algorithms usually enjoy better sample complexity than model-free algorithms from a novel representation complexity perspective: in some cases, the ground-truth rule (model) of the environment is simple to represent, while other quantities, such as $Q$-function, appear complex. We empirically corroborate our theory by comparing the approximation error of the transition kernel, reward function, and optimal $Q$-function in various Mujoco environments, which demonstrates that the approximation errors of the transition kernel and reward function are consistently lower than those of the optimal $Q$-function. To the best of our knowledge, this work is the first to study the circuit complexity of RL, which also provides a rigorous framework for future research.

Sample Complexity for Quadratic Bandits: Hessian Dependent Bounds and Optimal Algorithms

In stochastic zeroth-order optimization, a problem of practical relevance is understanding how to fully exploit the local geometry of the underlying objective function. We consider a fundamental setting in which the objective function is quadratic, and provide the first tight characterization of the optimal Hessian-dependent sample complexity. Our contribution is twofold. First, from an information-theoretic point of view, we prove tight lower bounds on Hessian-dependent complexities by introducing a concept called energy allocation, which captures the interaction between the searching algorithm and the geometry of objective functions. A matching upper bound is obtained by solving the optimal energy spectrum. Then, algorithmically, we show the existence of a Hessian-independent algorithm that universally achieves the asymptotic optimal sample complexities for all Hessian instances. The optimal sample complexities achieved by our algorithm remain valid for heavy-tailed noise distributions, which are enabled by a truncation method.

Evaluating and Incentivizing Diverse Data Contributions in Collaborative Learning

For a federated learning model to perform well, it is crucial to have a diverse and representative dataset. However, the data contributors may only be concerned with the performance on a specific subset of the population, which may not reflect the diversity of the wider population. This creates a tension between the principal (the FL platform designer) who cares about global performance and the agents (the data collectors) who care about local performance. In this work, we formulate this tension as a game between the principal and multiple agents, and focus on the linear experiment design problem to formally study their interaction. We show that the statistical criterion used to quantify the diversity of the data, as well as the choice of the federated learning algorithm used, has a significant effect on the resulting equilibrium. We leverage this to design simple optimal federated learning mechanisms that encourage data collectors to contribute data representative of the global population, thereby maximizing global performance.

Offline Reinforcement Learning with Realizability and Single-policy Concentrability

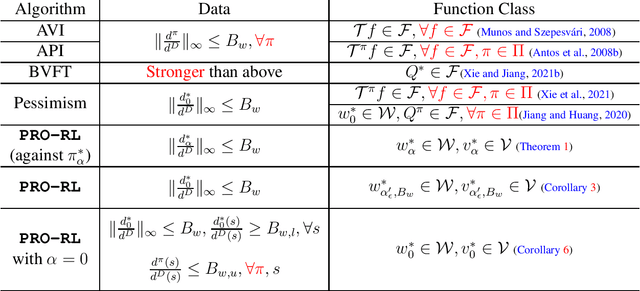
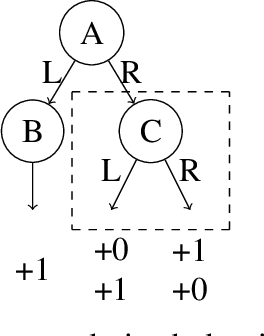
Sample-efficiency guarantees for offline reinforcement learning (RL) often rely on strong assumptions on both the function classes (e.g., Bellman-completeness) and the data coverage (e.g., all-policy concentrability). Despite the recent efforts on relaxing these assumptions, existing works are only able to relax one of the two factors, leaving the strong assumption on the other factor intact. As an important open problem, can we achieve sample-efficient offline RL with weak assumptions on both factors? In this paper we answer the question in the positive. We analyze a simple algorithm based on the primal-dual formulation of MDPs, where the dual variables (discounted occupancy) are modeled using a density-ratio function against offline data. With proper regularization, we show that the algorithm enjoys polynomial sample complexity, under only realizability and single-policy concentrability. We also provide alternative analyses based on different assumptions to shed light on the nature of primal-dual algorithms for offline RL.

Towards General Function Approximation in Zero-Sum Markov Games

This paper considers two-player zero-sum finite-horizon Markov games with simultaneous moves. The study focuses on the challenging settings where the value function or the model is parameterized by general function classes. Provably efficient algorithms for both decoupled and {coordinated} settings are developed. In the {decoupled} setting where the agent controls a single player and plays against an arbitrary opponent, we propose a new model-free algorithm. The sample complexity is governed by the Minimax Eluder dimension -- a new dimension of the function class in Markov games. As a special case, this method improves the state-of-the-art algorithm by a $\sqrt{d}$ factor in the regret when the reward function and transition kernel are parameterized with $d$-dimensional linear features. In the {coordinated} setting where both players are controlled by the agent, we propose a model-based algorithm and a model-free algorithm. In the model-based algorithm, we prove that sample complexity can be bounded by a generalization of Witness rank to Markov games. The model-free algorithm enjoys a $\sqrt{K}$-regret upper bound where $K$ is the number of episodes. Our algorithms are based on new techniques of alternate optimism.