GMKF: Generalized Moment Kalman Filter for Polynomial Systems with Arbitrary Noise

This paper develops a new filtering approach for state estimation in polynomial systems corrupted by arbitrary noise, which commonly arise in robotics. We first consider a batch setup where we perform state estimation using all data collected from the initial to the current time. We formulate the batch state estimation problem as a Polynomial Optimization Problem (POP) and relax the assumption of Gaussian noise by specifying a finite number of moments of the noise. We solve the resulting POP using a moment relaxation and prove that under suitable conditions on the rank of the relaxation, (i) we can extract a provably optimal estimate from the moment relaxation, and (ii) we can obtain a belief representation from the dual (sum-of-squares) relaxation. We then turn our attention to the filtering setup and apply similar insights to develop a GMKF for recursive state estimation in polynomial systems with arbitrary noise. The GMKF formulates the prediction and update steps as POPs and solves them using moment relaxations, carrying over a possibly non-Gaussian belief. In the linear-Gaussian case, GMKF reduces to the standard Kalman Filter. We demonstrate that GMKF performs well under highly non-Gaussian noise and outperforms common alternatives, including the Extended and Unscented Kalman Filter, and their variants on matrix Lie group.

Convex Risk Bounded Continuous-Time Trajectory Planning and Tube Design in Uncertain Nonconvex Environments

In this paper, we address the trajectory planning problem in uncertain nonconvex static and dynamic environments that contain obstacles with probabilistic location, size, and geometry. To address this problem, we provide a risk bounded trajectory planning method that looks for continuous-time trajectories with guaranteed bounded risk over the planning time horizon. Risk is defined as the probability of collision with uncertain obstacles. Existing approaches to address risk bounded trajectory planning problems either are limited to Gaussian uncertainties and convex obstacles or rely on sampling-based methods that need uncertainty samples and time discretization. To address the risk bounded trajectory planning problem, we leverage the notion of risk contours to transform the risk bounded planning problem into a deterministic optimization problem. Risk contours are the set of all points in the uncertain environment with guaranteed bounded risk. The obtained deterministic optimization is, in general, nonlinear and nonconvex time-varying optimization. We provide convex methods based on sum-of-squares optimization to efficiently solve the obtained nonconvex time-varying optimization problem and obtain the continuous-time risk bounded trajectories without time discretization. The provided approach deals with arbitrary (and known) probabilistic uncertainties, nonconvex and nonlinear, static and dynamic obstacles, and is suitable for online trajectory planning problems. In addition, we provide convex methods based on sum-of-squares optimization to build the max-sized tube with respect to its parameterization along the trajectory so that any state inside the tube is guaranteed to have bounded risk.

Convex Geometric Motion Planning on Lie Groups via Moment Relaxation

This paper reports a novel result: with proper robot models on matrix Lie groups, one can formulate the kinodynamic motion planning problem for rigid body systems as \emph{exact} polynomial optimization problems that can be relaxed as semidefinite programming (SDP). Due to the nonlinear rigid body dynamics, the motion planning problem for rigid body systems is nonconvex. Existing global optimization-based methods do not properly deal with the configuration space of the 3D rigid body; thus, they do not scale well to long-horizon planning problems. We use Lie groups as the configuration space in our formulation and apply the variational integrator to formulate the forced rigid body systems as quadratic polynomials. Then we leverage Lasserre's hierarchy to obtain the globally optimal solution via SDP. By constructing the motion planning problem in a sparse manner, the results show that the proposed algorithm has \emph{linear} complexity with respect to the planning horizon. This paper demonstrates the proposed method can provide rank-one optimal solutions at relaxation order two for most of the testing cases of 1) 3D drone landing using the full dynamics model and 2) inverse kinematics for serial manipulators.

Real-Time Tube-Based Non-Gaussian Risk Bounded Motion Planning for Stochastic Nonlinear Systems in Uncertain Environments via Motion Primitives

We consider the motion planning problem for stochastic nonlinear systems in uncertain environments. More precisely, in this problem the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles. Obstacles can be of arbitrary shape, can deform, and can move. All uncertainties do not necessarily have Gaussian distribution. This general setting has been considered and solved in [1]. In addition to the assumptions above, in this paper, we consider long-term tasks, where the planning method in [1] would fail, as the uncertainty of the system states grows too large over a long time horizon. Unlike [1], we present a real-time online motion planning algorithm. We build discrete-time motion primitives and their corresponding continuous-time tubes offline, so that almost all system states of each motion primitive are guaranteed to stay inside the corresponding tube. We convert probabilistic safety constraints into a set of deterministic constraints called risk contours. During online execution, we verify the safety of the tubes against deterministic risk contours using sum-of-squares (SOS) programming. The provided SOS-based method verifies the safety of the tube in the presence of uncertain obstacles without the need for uncertainty samples and time discretization in real-time. By bounding the probability the system states staying inside the tube and bounding the probability of the tube colliding with obstacles, our approach guarantees bounded probability of system states colliding with obstacles. We demonstrate our approach on several long-term robotics tasks.

Non-Gaussian Uncertainty Minimization Based Control of Stochastic Nonlinear Robotic Systems

In this paper, we consider the closed-loop control problem of nonlinear robotic systems in the presence of probabilistic uncertainties and disturbances. More precisely, we design a state feedback controller that minimizes deviations of the states of the system from the nominal state trajectories due to uncertainties and disturbances. Existing approaches to address the control problem of probabilistic systems are limited to particular classes of uncertainties and systems such as Gaussian uncertainties and processes and linearized systems. We present an approach that deals with nonlinear dynamics models and arbitrary known probabilistic uncertainties. We formulate the controller design problem as an optimization problem in terms of statistics of the probability distributions including moments and characteristic functions. In particular, in the provided optimization problem, we use moments and characteristic functions to propagate uncertainties throughout the nonlinear motion model of robotic systems. In order to reduce the tracking deviations, we minimize the uncertainty of the probabilistic states around the nominal trajectory by minimizing the trace and the determinant of the covariance matrix of the probabilistic states. To obtain the state feedback gains, we solve deterministic optimization problems in terms of moments, characteristic functions, and state feedback gains using off-the-shelf interior-point optimization solvers. To illustrate the performance of the proposed method, we compare our method with existing probabilistic control methods.

Chance-Constrained Trajectory Optimization for High-DOF Robots in Uncertain Environments

Many practical applications of robotics require systems that can operate safely despite uncertainty. In the context of motion planning, two types of uncertainty are particularly important when planning safe robot trajectories. The first is environmental uncertainty -- uncertainty in the locations of nearby obstacles, stemming from sensor noise or (in the case of obstacles' future locations) prediction error. The second class of uncertainty is uncertainty in the robots own state, typically caused by tracking or estimation error. To achieve high levels of safety, it is necessary for robots to consider both of these sources of uncertainty. In this paper, we propose a risk-bounded trajectory optimization algorithm, known as Sequential Convex Optimization with Risk Optimization (SCORA), to solve chance-constrained motion planning problems despite both environmental uncertainty and tracking error. Through experiments in simulation, we demonstrate that SCORA significantly outperforms state-of-the-art risk-aware motion planners both in planning time and in the safety of the resulting trajectories.

Moment-based Kalman Filter: Nonlinear Kalman Filtering with Exact Moment Propagation

This paper develops a new nonlinear filter, called Moment-based Kalman Filter (MKF), using the exact moment propagation method. Existing state estimation methods use linearization techniques or sampling points to compute approximate values of moments. However, moment propagation of probability distributions of random variables through nonlinear process and measurement models play a key role in the development of state estimation and directly affects their performance. The proposed moment propagation procedure can compute exact moments for non-Gaussian as well as non-independent Gaussian random variables. Thus, MKF can propagate exact moments of uncertain state variables up to any desired order. MKF is derivative-free and does not require tuning parameters. Moreover, MKF has the same computation time complexity as the extended or unscented Kalman filters, i.e., EKF and UKF. The experimental evaluations show that MKF is the preferred filter in comparison to EKF and UKF and outperforms both filters in non-Gaussian noise regimes.

Non-Gaussian Risk Bounded Trajectory Optimization for Stochastic Nonlinear Systems in Uncertain Environments

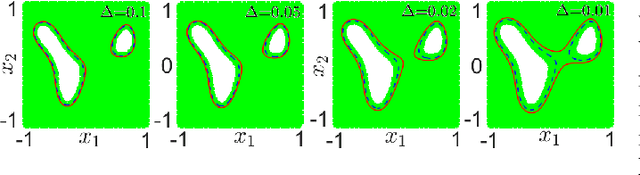
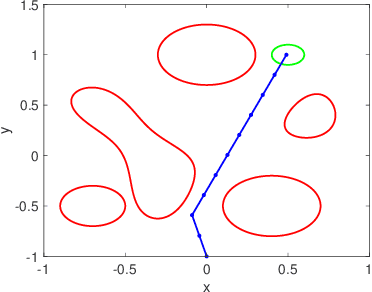
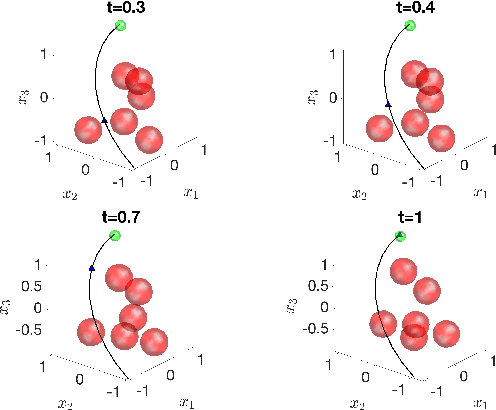
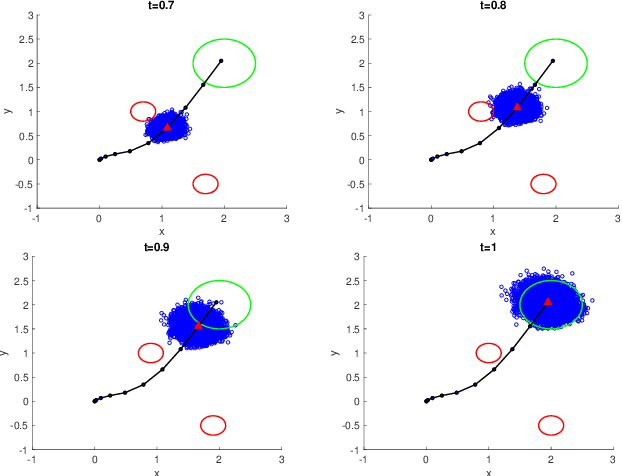
We address the risk bounded trajectory optimization problem of stochastic nonlinear robotic systems. More precisely, we consider the motion planning problem in which the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles with arbitrary probabilistic distributions. The goal is to plan a sequence of control inputs for the robot to navigate to the target while bounding the probability of colliding with obstacles. Existing approaches to address risk bounded trajectory optimization problems are limited to particular classes of models and uncertainties such as Gaussian linear problems. In this paper, we deal with stochastic nonlinear models, nonlinear safety constraints, and arbitrary probabilistic uncertainties, the most general setting ever considered. To address the risk bounded trajectory optimization problem, we first formulate the problem as an optimization problem with stochastic dynamics equations and chance constraints. We then convert probabilistic constraints and stochastic dynamics constraints on random variables into a set of deterministic constraints on the moments of state probability distributions. Finally, we solve the resulting deterministic optimization problem using nonlinear optimization solvers and get a sequence of control inputs. To our best knowledge, it is the first time that the motion planning problem to such a general extent is considered and solved. To illustrate the performance of the proposed method, we provide several robotics examples.

TIP: Task-Informed Motion Prediction for Intelligent Systems

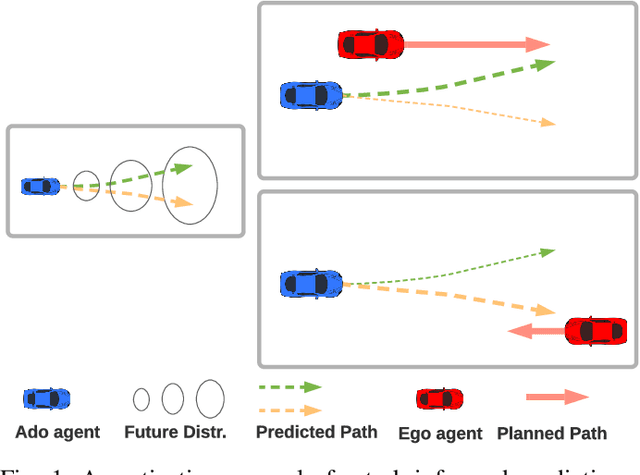
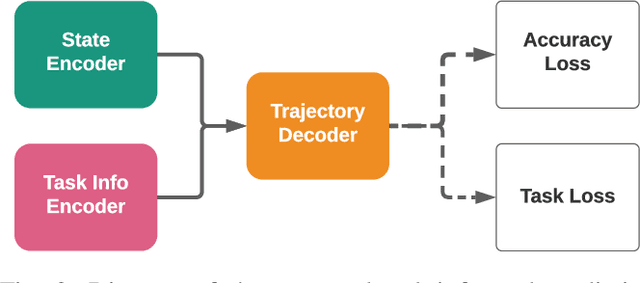
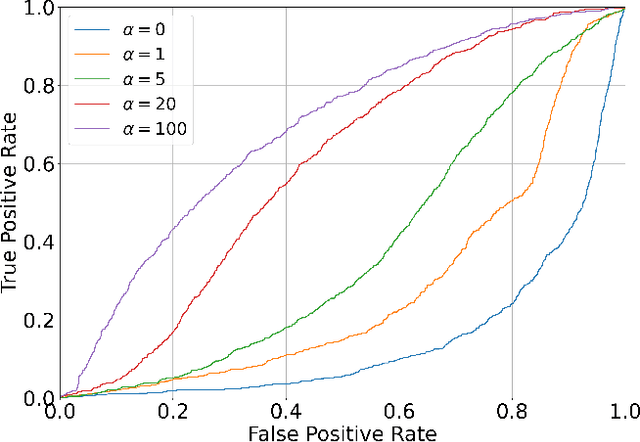
Motion prediction is important for intelligent driving systems, providing the future distributions of road agent behaviors and supporting various decision making tasks. Existing motion predictors are often optimized and evaluated via task-agnostic measures based on prediction accuracy. Such measures fail to account for the use of prediction in downstream tasks, and could result in sub-optimal task performance. We propose a task-informed motion prediction framework that jointly reasons about prediction accuracy and task utility, to better support downstream tasks through its predictions. The task utility function does not require the full task information, but rather a specification of the utility of the task, resulting in predictors that serve a wide range of downstream tasks. We demonstrate our framework on two use cases of task utilities, in the context of autonomous driving and parallel autonomy, and show the advantage of task-informed predictors over task-agnostic ones on the Waymo Open Motion dataset.

HYPER: Learned Hybrid Trajectory Prediction via Factored Inference and Adaptive Sampling

Modeling multi-modal high-level intent is important for ensuring diversity in trajectory prediction. Existing approaches explore the discrete nature of human intent before predicting continuous trajectories, to improve accuracy and support explainability. However, these approaches often assume the intent to remain fixed over the prediction horizon, which is problematic in practice, especially over longer horizons. To overcome this limitation, we introduce HYPER, a general and expressive hybrid prediction framework that models evolving human intent. By modeling traffic agents as a hybrid discrete-continuous system, our approach is capable of predicting discrete intent changes over time. We learn the probabilistic hybrid model via a maximum likelihood estimation problem and leverage neural proposal distributions to sample adaptively from the exponentially growing discrete space. The overall approach affords a better trade-off between accuracy and coverage. We train and validate our model on the Argoverse dataset, and demonstrate its effectiveness through comprehensive ablation studies and comparisons with state-of-the-art models.