Bisimulation metric for Model Predictive Control

Model-based reinforcement learning has shown promise for improving sample efficiency and decision-making in complex environments. However, existing methods face challenges in training stability, robustness to noise, and computational efficiency. In this paper, we propose Bisimulation Metric for Model Predictive Control (BS-MPC), a novel approach that incorporates bisimulation metric loss in its objective function to directly optimize the encoder. This time-step-wise direct optimization enables the learned encoder to extract intrinsic information from the original state space while discarding irrelevant details and preventing the gradients and errors from diverging. BS-MPC improves training stability, robustness against input noise, and computational efficiency by reducing training time. We evaluate BS-MPC on both continuous control and image-based tasks from the DeepMind Control Suite, demonstrating superior performance and robustness compared to state-of-the-art baseline methods.

Strategically Conservative Q-Learning

Offline reinforcement learning (RL) is a compelling paradigm to extend RL's practical utility by leveraging pre-collected, static datasets, thereby avoiding the limitations associated with collecting online interactions. The major difficulty in offline RL is mitigating the impact of approximation errors when encountering out-of-distribution (OOD) actions; doing so ineffectively will lead to policies that prefer OOD actions, which can lead to unexpected and potentially catastrophic results. Despite the variety of works proposed to address this issue, they tend to excessively suppress the value function in and around OOD regions, resulting in overly pessimistic value estimates. In this paper, we propose a novel framework called Strategically Conservative Q-Learning (SCQ) that distinguishes between OOD data that is easy and hard to estimate, ultimately resulting in less conservative value estimates. Our approach exploits the inherent strengths of neural networks to interpolate, while carefully navigating their limitations in extrapolation, to obtain pessimistic yet still property calibrated value estimates. Theoretical analysis also shows that the value function learned by SCQ is still conservative, but potentially much less so than that of Conservative Q-learning (CQL). Finally, extensive evaluation on the D4RL benchmark tasks shows our proposed method outperforms state-of-the-art methods. Our code is available through \url{https://github.com/purewater0901/SCQ}.

Moment-based Kalman Filter: Nonlinear Kalman Filtering with Exact Moment Propagation

This paper develops a new nonlinear filter, called Moment-based Kalman Filter (MKF), using the exact moment propagation method. Existing state estimation methods use linearization techniques or sampling points to compute approximate values of moments. However, moment propagation of probability distributions of random variables through nonlinear process and measurement models play a key role in the development of state estimation and directly affects their performance. The proposed moment propagation procedure can compute exact moments for non-Gaussian as well as non-independent Gaussian random variables. Thus, MKF can propagate exact moments of uncertain state variables up to any desired order. MKF is derivative-free and does not require tuning parameters. Moreover, MKF has the same computation time complexity as the extended or unscented Kalman filters, i.e., EKF and UKF. The experimental evaluations show that MKF is the preferred filter in comparison to EKF and UKF and outperforms both filters in non-Gaussian noise regimes.

Chance-Constrained Iterative Linear-Quadratic Stochastic Games

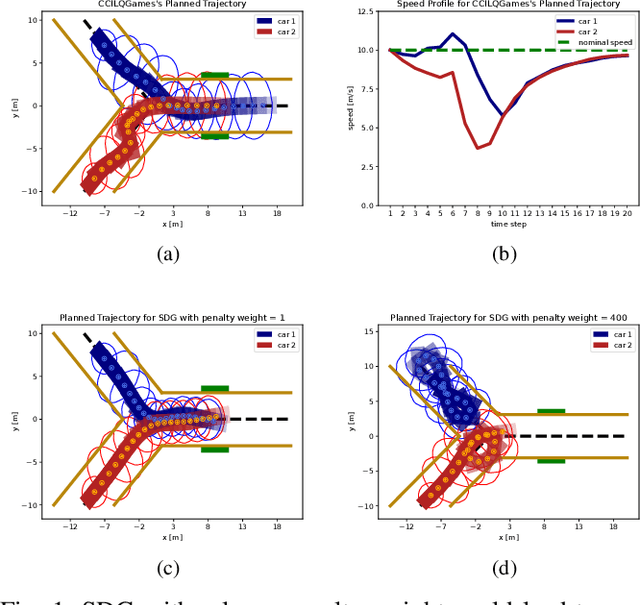
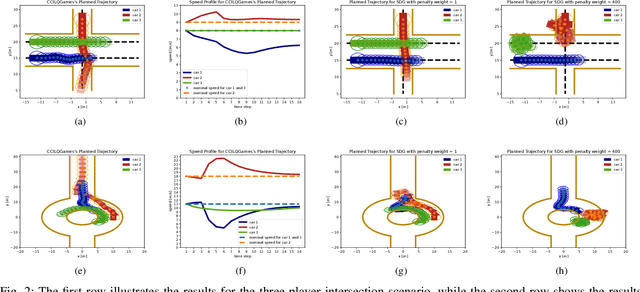
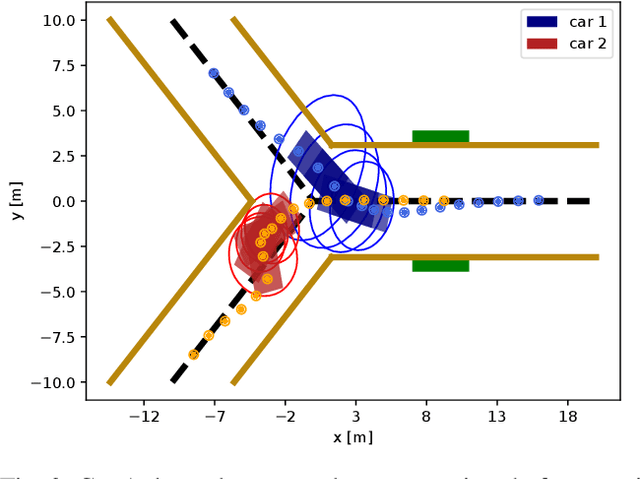
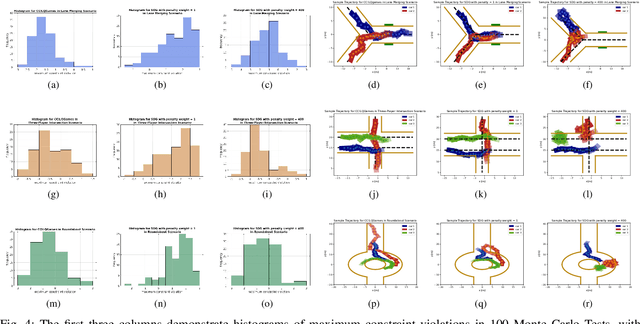
Dynamic game arises as a powerful paradigm for multi-robot planning, for which the safety constraints satisfaction is crucial. Constrained stochastic games are of particular interest, as real-world robots need to operate and satisfy constraints under uncertainty. Existing methods for solving stochastic games handle constraints using soft penalties with hand-tuned weights. However, finding a suitable penalty weight is non-trivial and requires trial and error. In this paper, we propose the chance-constrained iterative linear-quadratic stochastic games (CCILQGames) algorithm. CCILQGames solves chance-constrained stochastic games using the augmented Lagrangian method, with the merit of automatically finding a suitable penalty weight. We evaluate our algorithm in three autonomous driving scenarios, including merge, intersection, and roundabout. Experimental results and Monte Carlo tests show that CCILQGames could generate safe and interactive strategies in stochastic environments.

Jerk Constrained Velocity Planning for an Autonomous Vehicle: Linear Programming Approach

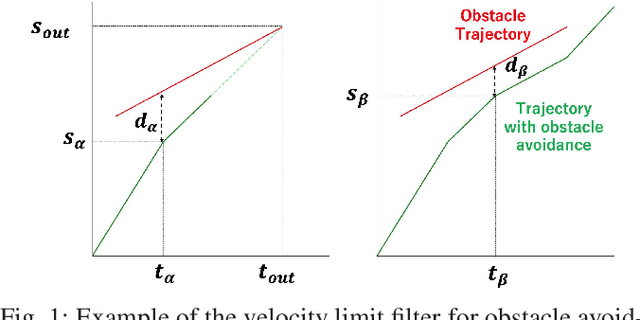
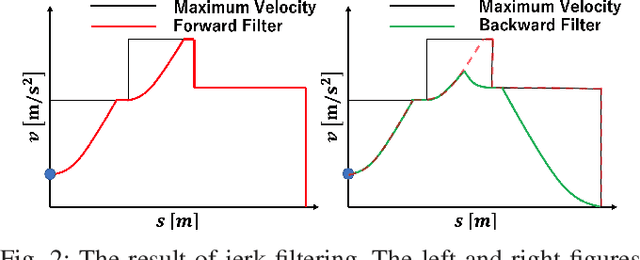
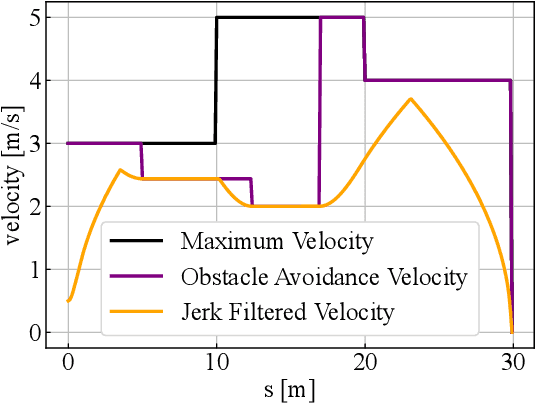
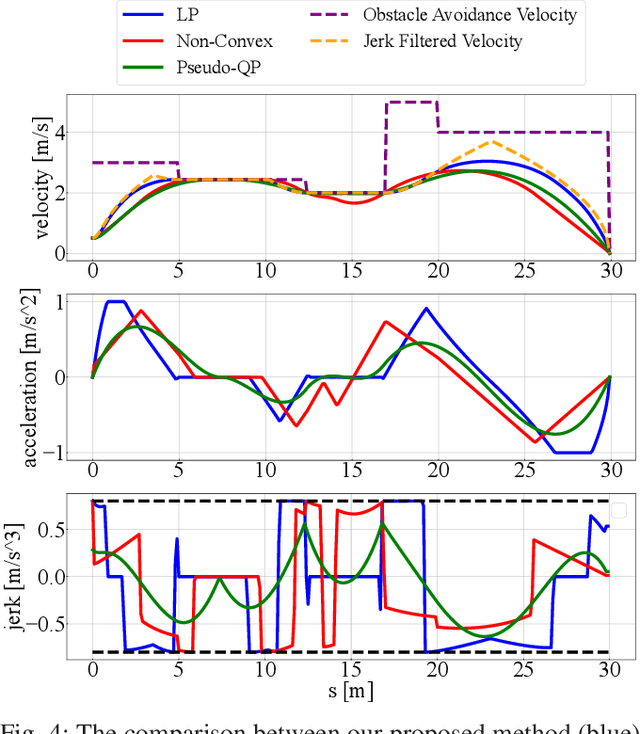
Velocity Planning for self-driving vehicles in a complex environment is one of the most challenging tasks. It must satisfy the following three requirements: safety with regards to collisions; respect of the maximum velocity limits defined by the traffic rules; comfort of the passengers. In order to achieve these goals, the jerk and dynamic objects should be considered, however, it makes the problem as complex as a non-convex optimization problem. In this paper, we propose a linear programming (LP) based velocity planning method with jerk limit and obstacle avoidance constraints for an autonomous driving system. To confirm the efficiency of the proposed method, a comparison is made with several optimization-based approaches, and we show that our method can generate a velocity profile which satisfies the aforementioned requirements more efficiently than the compared methods. In addition, we tested our algorithm on a real vehicle at a test field to validate the effectiveness of the proposed method.

Constrained Iterative LQG for Real-Time Chance-Constrained Gaussian Belief Space Planning

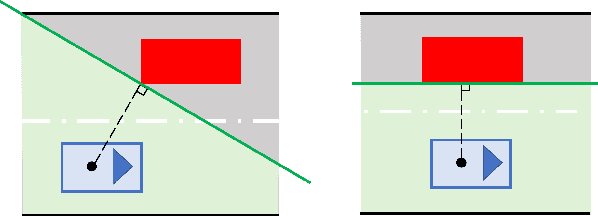
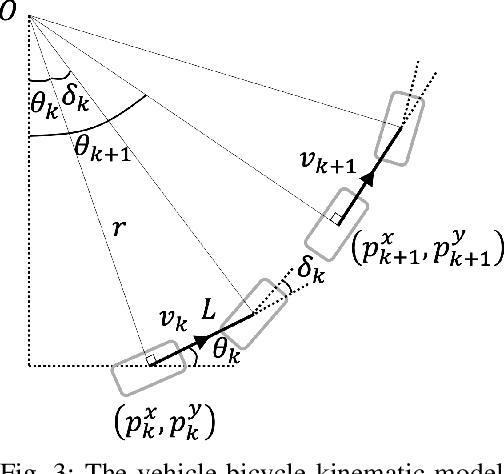
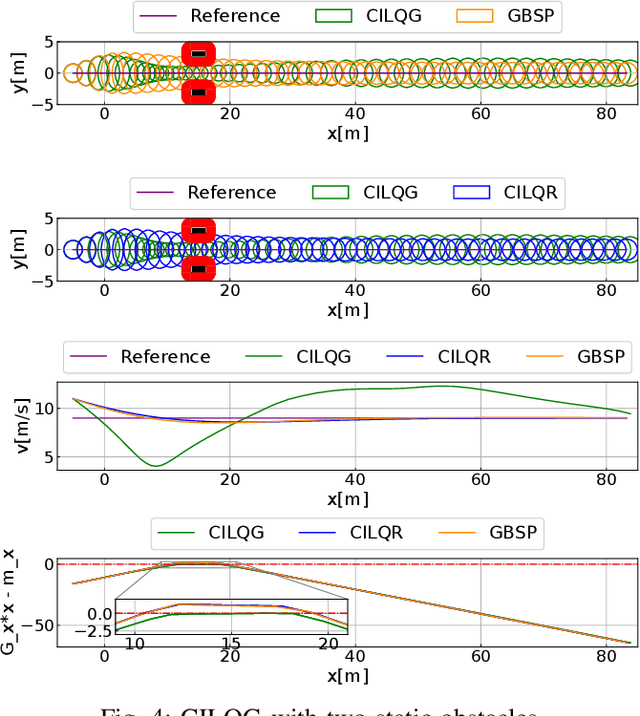
Motion planning under uncertainty is of significant importance for safety-critical systems such as autonomous vehicles. Such systems have to satisfy necessary constraints (e.g., collision avoidance) with potential uncertainties coming from either disturbed system dynamics or noisy sensor measurements. However, existing motion planning methods cannot efficiently find the robust optimal solutions under general nonlinear and non-convex settings. In this paper, we formulate such problem as chance-constrained Gaussian belief space planning and propose the constrained iterative Linear Quadratic Gaussian (CILQG) algorithm as a real-time solution. In this algorithm, we iteratively calculate a Gaussian approximation of the belief and transform the chance-constraints. We evaluate the effectiveness of our method in simulations of autonomous driving planning tasks with static and dynamic obstacles. Results show that CILQG can handle uncertainties more appropriately and has faster computation time than baseline methods.