Joint Differentiable Optimization and Verification for Certified Reinforcement Learning

In model-based reinforcement learning for safety-critical control systems, it is important to formally certify system properties (e.g., safety, stability) under the learned controller. However, as existing methods typically apply formal verification \emph{after} the controller has been learned, it is sometimes difficult to obtain any certificate, even after many iterations between learning and verification. To address this challenge, we propose a framework that jointly conducts reinforcement learning and formal verification by formulating and solving a novel bilevel optimization problem, which is differentiable by the gradients from the value function and certificates. Experiments on a variety of examples demonstrate the significant advantages of our framework over the model-based stochastic value gradient (SVG) method and the model-free proximal policy optimization (PPO) method in finding feasible controllers with barrier functions and Lyapunov functions that ensure system safety and stability.

Exponential Family Model-Based Reinforcement Learning via Score Matching

We propose an optimistic model-based algorithm, dubbed SMRL, for finite-horizon episodic reinforcement learning (RL) when the transition model is specified by exponential family distributions with $d$ parameters and the reward is bounded and known. SMRL uses score matching, an unnormalized density estimation technique that enables efficient estimation of the model parameter by ridge regression. Under standard regularity assumptions, SMRL achieves $\tilde O(d\sqrt{H^3T})$ online regret, where $H$ is the length of each episode and $T$ is the total number of interactions (ignoring polynomial dependence on structural scale parameters).

Wasserstein Flow Meets Replicator Dynamics: A Mean-Field Analysis of Representation Learning in Actor-Critic

Actor-critic (AC) algorithms, empowered by neural networks, have had significant empirical success in recent years. However, most of the existing theoretical support for AC algorithms focuses on the case of linear function approximations, or linearized neural networks, where the feature representation is fixed throughout training. Such a limitation fails to capture the key aspect of representation learning in neural AC, which is pivotal in practical problems. In this work, we take a mean-field perspective on the evolution and convergence of feature-based neural AC. Specifically, we consider a version of AC where the actor and critic are represented by overparameterized two-layer neural networks and are updated with two-timescale learning rates. The critic is updated by temporal-difference (TD) learning with a larger stepsize while the actor is updated via proximal policy optimization (PPO) with a smaller stepsize. In the continuous-time and infinite-width limiting regime, when the timescales are properly separated, we prove that neural AC finds the globally optimal policy at a sublinear rate. Additionally, we prove that the feature representation induced by the critic network is allowed to evolve within a neighborhood of the initial one.

Can Reinforcement Learning Find Stackelberg-Nash Equilibria in General-Sum Markov Games with Myopic Followers?

We study multi-player general-sum Markov games with one of the players designated as the leader and the other players regarded as followers. In particular, we focus on the class of games where the followers are myopic, i.e., they aim to maximize their instantaneous rewards. For such a game, our goal is to find a Stackelberg-Nash equilibrium (SNE), which is a policy pair $(\pi^*, \nu^*)$ such that (i) $\pi^*$ is the optimal policy for the leader when the followers always play their best response, and (ii) $\nu^*$ is the best response policy of the followers, which is a Nash equilibrium of the followers' game induced by $\pi^*$. We develop sample-efficient reinforcement learning (RL) algorithms for solving for an SNE in both online and offline settings. Our algorithms are optimistic and pessimistic variants of least-squares value iteration, and they are readily able to incorporate function approximation tools in the setting of large state spaces. Furthermore, for the case with linear function approximation, we prove that our algorithms achieve sublinear regret and suboptimality under online and offline setups respectively. To the best of our knowledge, we establish the first provably efficient RL algorithms for solving for SNEs in general-sum Markov games with myopic followers.

ElegantRL-Podracer: Scalable and Elastic Library for Cloud-Native Deep Reinforcement Learning

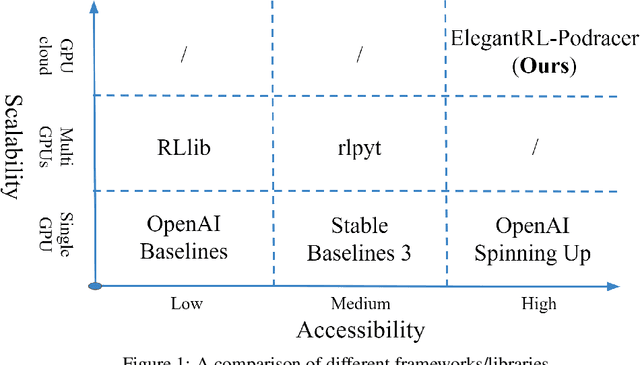
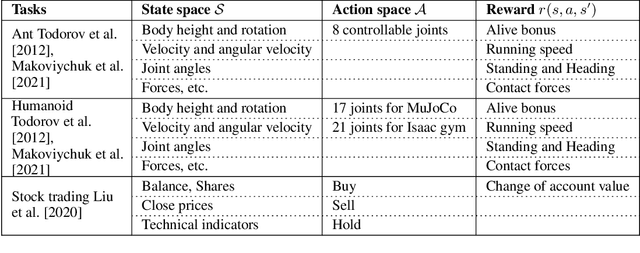
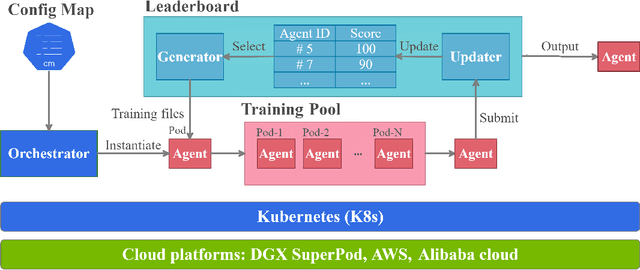
Deep reinforcement learning (DRL) has revolutionized learning and actuation in applications such as game playing and robotic control. The cost of data collection, i.e., generating transitions from agent-environment interactions, remains a major challenge for wider DRL adoption in complex real-world problems. Following a cloud-native paradigm to train DRL agents on a GPU cloud platform is a promising solution. In this paper, we present a scalable and elastic library ElegantRL-podracer for cloud-native deep reinforcement learning, which efficiently supports millions of GPU cores to carry out massively parallel training at multiple levels. At a high-level, ElegantRL-podracer employs a tournament-based ensemble scheme to orchestrate the training process on hundreds or even thousands of GPUs, scheduling the interactions between a leaderboard and a training pool with hundreds of pods. At a low-level, each pod simulates agent-environment interactions in parallel by fully utilizing nearly 7,000 GPU CUDA cores in a single GPU. Our ElegantRL-podracer library features high scalability, elasticity and accessibility by following the development principles of containerization, microservices and MLOps. Using an NVIDIA DGX SuperPOD cloud, we conduct extensive experiments on various tasks in locomotion and stock trading and show that ElegantRL-podracer substantially outperforms RLlib. Our codes are available on GitHub.

Exponential Bellman Equation and Improved Regret Bounds for Risk-Sensitive Reinforcement Learning

We study risk-sensitive reinforcement learning (RL) based on the entropic risk measure. Although existing works have established non-asymptotic regret guarantees for this problem, they leave open an exponential gap between the upper and lower bounds. We identify the deficiencies in existing algorithms and their analysis that result in such a gap. To remedy these deficiencies, we investigate a simple transformation of the risk-sensitive Bellman equations, which we call the exponential Bellman equation. The exponential Bellman equation inspires us to develop a novel analysis of Bellman backup procedures in risk-sensitive RL algorithms, and further motivates the design of a novel exploration mechanism. We show that these analytic and algorithmic innovations together lead to improved regret upper bounds over existing ones.

SCORE: Spurious COrrelation REduction for Offline Reinforcement Learning

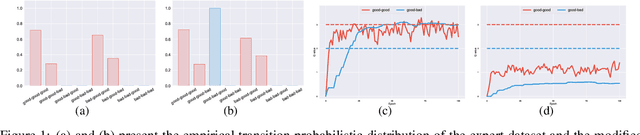
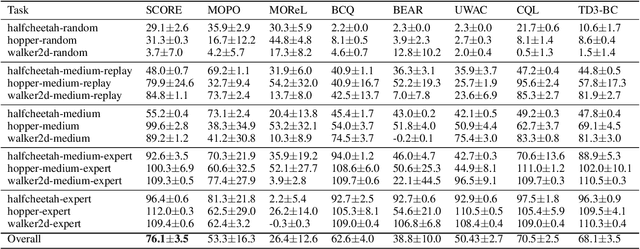
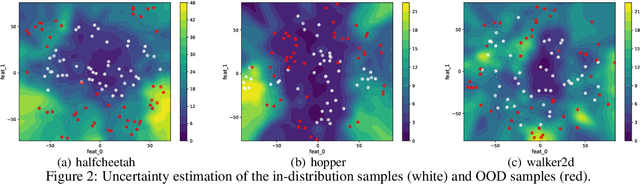
Offline reinforcement learning (RL) aims to learn the optimal policy from a pre-collected dataset without online interactions. Most of the existing studies focus on distributional shift caused by out-of-distribution actions. However, even in-distribution actions can raise serious problems. Since the dataset only contains limited information about the underlying model, offline RL is vulnerable to spurious correlations, i.e., the agent tends to prefer actions that by chance lead to high returns, resulting in a highly suboptimal policy. To address such a challenge, we propose a practical and theoretically guaranteed algorithm SCORE that reduces spurious correlations by combing an uncertainty penalty into policy evaluation. We show that this is consistent with the pessimism principle studied in theory, and the proposed algorithm converges to the optimal policy with a sublinear rate under mild assumptions. By conducting extensive experiments on existing benchmarks, we show that SCORE not only benefits from a solid theory but also obtains strong empirical results on a variety of tasks.

On Reward-Free RL with Kernel and Neural Function Approximations: Single-Agent MDP and Markov Game

To achieve sample efficiency in reinforcement learning (RL), it necessitates efficiently exploring the underlying environment. Under the offline setting, addressing the exploration challenge lies in collecting an offline dataset with sufficient coverage. Motivated by such a challenge, we study the reward-free RL problem, where an agent aims to thoroughly explore the environment without any pre-specified reward function. Then, given any extrinsic reward, the agent computes the policy via a planning algorithm with offline data collected in the exploration phase. Moreover, we tackle this problem under the context of function approximation, leveraging powerful function approximators. Specifically, we propose to explore via an optimistic variant of the value-iteration algorithm incorporating kernel and neural function approximations, where we adopt the associated exploration bonus as the exploration reward. Moreover, we design exploration and planning algorithms for both single-agent MDPs and zero-sum Markov games and prove that our methods can achieve $\widetilde{\mathcal{O}}(1 /\varepsilon^2)$ sample complexity for generating a $\varepsilon$-suboptimal policy or $\varepsilon$-approximate Nash equilibrium when given an arbitrary extrinsic reward. To the best of our knowledge, we establish the first provably efficient reward-free RL algorithm with kernel and neural function approximators.

Optimistic Policy Optimization is Provably Efficient in Non-stationary MDPs

We study episodic reinforcement learning (RL) in non-stationary linear kernel Markov decision processes (MDPs). In this setting, both the reward function and the transition kernel are linear with respect to the given feature maps and are allowed to vary over time, as long as their respective parameter variations do not exceed certain variation budgets. We propose the $\underline{\text{p}}$eriodically $\underline{\text{r}}$estarted $\underline{\text{o}}$ptimistic $\underline{\text{p}}$olicy $\underline{\text{o}}$ptimization algorithm (PROPO), which is an optimistic policy optimization algorithm with linear function approximation. PROPO features two mechanisms: sliding-window-based policy evaluation and periodic-restart-based policy improvement, which are tailored for policy optimization in a non-stationary environment. In addition, only utilizing the technique of sliding window, we propose a value-iteration algorithm. We establish dynamic upper bounds for the proposed methods and a matching minimax lower bound which shows the (near-) optimality of the proposed methods. To our best knowledge, PROPO is the first provably efficient policy optimization algorithm that handles non-stationarity.

Inducing Equilibria via Incentives: Simultaneous Design-and-Play Finds Global Optima

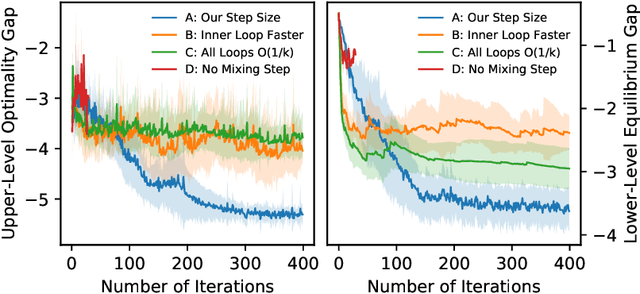
To regulate a social system comprised of self-interested agents, economic incentives (e.g., taxes, tolls, and subsidies) are often required to induce a desirable outcome. This incentive design problem naturally possesses a bi-level structure, in which an upper-level "designer" modifies the payoffs of the agents with incentives while anticipating the response of the agents at the lower level, who play a non-cooperative game that converges to an equilibrium. The existing bi-level optimization algorithms developed in machine learning raise a dilemma when applied to this problem: anticipating how incentives affect the agents at equilibrium requires solving the equilibrium problem repeatedly, which is computationally inefficient; bypassing the time-consuming step of equilibrium-finding can reduce the computational cost, but may lead the designer to a sub-optimal solution. To address such a dilemma, we propose a method that tackles the designer's and agents' problems simultaneously in a single loop. In particular, at each iteration, both the designer and the agents only move one step based on the first-order information. In the proposed scheme, although the designer does not solve the equilibrium problem repeatedly, it can anticipate the overall influence of the incentives on the agents, which guarantees optimality. We prove that the algorithm converges to the global optima at a sublinear rate for a broad class of games.