Embed to Control Partially Observed Systems: Representation Learning with Provable Sample Efficiency

Reinforcement learning in partially observed Markov decision processes (POMDPs) faces two challenges. (i) It often takes the full history to predict the future, which induces a sample complexity that scales exponentially with the horizon. (ii) The observation and state spaces are often continuous, which induces a sample complexity that scales exponentially with the extrinsic dimension. Addressing such challenges requires learning a minimal but sufficient representation of the observation and state histories by exploiting the structure of the POMDP. To this end, we propose a reinforcement learning algorithm named Embed to Control (ETC), which learns the representation at two levels while optimizing the policy.~(i) For each step, ETC learns to represent the state with a low-dimensional feature, which factorizes the transition kernel. (ii) Across multiple steps, ETC learns to represent the full history with a low-dimensional embedding, which assembles the per-step feature. We integrate (i) and (ii) in a unified framework that allows a variety of estimators (including maximum likelihood estimators and generative adversarial networks). For a class of POMDPs with a low-rank structure in the transition kernel, ETC attains an $O(1/\epsilon^2)$ sample complexity that scales polynomially with the horizon and the intrinsic dimension (that is, the rank). Here $\epsilon$ is the optimality gap. To our best knowledge, ETC is the first sample-efficient algorithm that bridges representation learning and policy optimization in POMDPs with infinite observation and state spaces.

Human-in-the-loop: Provably Efficient Preference-based Reinforcement Learning with General Function Approximation

We study human-in-the-loop reinforcement learning (RL) with trajectory preferences, where instead of receiving a numeric reward at each step, the agent only receives preferences over trajectory pairs from a human overseer. The goal of the agent is to learn the optimal policy which is most preferred by the human overseer. Despite the empirical successes, the theoretical understanding of preference-based RL (PbRL) is only limited to the tabular case. In this paper, we propose the first optimistic model-based algorithm for PbRL with general function approximation, which estimates the model using value-targeted regression and calculates the exploratory policies by solving an optimistic planning problem. Our algorithm achieves the regret of $\tilde{O} (\operatorname{poly}(d H) \sqrt{K} )$, where $d$ is the complexity measure of the transition and preference model depending on the Eluder dimension and log-covering numbers, $H$ is the planning horizon, $K$ is the number of episodes, and $\tilde O(\cdot)$ omits logarithmic terms. Our lower bound indicates that our algorithm is near-optimal when specialized to the linear setting. Furthermore, we extend the PbRL problem by formulating a novel problem called RL with $n$-wise comparisons, and provide the first sample-efficient algorithm for this new setting. To the best of our knowledge, this is the first theoretical result for PbRL with (general) function approximation.

Pessimism meets VCG: Learning Dynamic Mechanism Design via Offline Reinforcement Learning

Dynamic mechanism design has garnered significant attention from both computer scientists and economists in recent years. By allowing agents to interact with the seller over multiple rounds, where agents' reward functions may change with time and are state dependent, the framework is able to model a rich class of real world problems. In these works, the interaction between agents and sellers are often assumed to follow a Markov Decision Process (MDP). We focus on the setting where the reward and transition functions of such an MDP are not known a priori, and we are attempting to recover the optimal mechanism using an a priori collected data set. In the setting where the function approximation is employed to handle large state spaces, with only mild assumptions on the expressiveness of the function class, we are able to design a dynamic mechanism using offline reinforcement learning algorithms. Moreover, learned mechanisms approximately have three key desiderata: efficiency, individual rationality, and truthfulness. Our algorithm is based on the pessimism principle and only requires a mild assumption on the coverage of the offline data set. To the best of our knowledge, our work provides the first offline RL algorithm for dynamic mechanism design without assuming uniform coverage.

Sample-Efficient Reinforcement Learning for POMDPs with Linear Function Approximations

Despite the success of reinforcement learning (RL) for Markov decision processes (MDPs) with function approximation, most RL algorithms easily fail if the agent only has partial observations of the state. Such a setting is often modeled as a partially observable Markov decision process (POMDP). Existing sample-efficient algorithms for POMDPs are restricted to the tabular setting where the state and observation spaces are finite. In this paper, we make the first attempt at tackling the tension between function approximation and partial observability. In specific, we focus on a class of undercomplete POMDPs with linear function approximations, which allows the state and observation spaces to be infinite. For such POMDPs, we show that the optimal policy and value function can be characterized by a sequence of finite-memory Bellman operators. We propose an RL algorithm that constructs optimistic estimators of these operators via reproducing kernel Hilbert space (RKHS) embedding. Moreover, we theoretically prove that the proposed algorithm finds an $\varepsilon$-optimal policy with $\tilde O (1/\varepsilon^2)$ episodes of exploration. Also, this sample complexity only depends on the intrinsic dimension of the POMDP polynomially and is independent of the size of the state and observation spaces. To our best knowledge, we develop the first provably sample-efficient algorithm for POMDPs with function approximation.

Learn to Match with No Regret: Reinforcement Learning in Markov Matching Markets

We study a Markov matching market involving a planner and a set of strategic agents on the two sides of the market. At each step, the agents are presented with a dynamical context, where the contexts determine the utilities. The planner controls the transition of the contexts to maximize the cumulative social welfare, while the agents aim to find a myopic stable matching at each step. Such a setting captures a range of applications including ridesharing platforms. We formalize the problem by proposing a reinforcement learning framework that integrates optimistic value iteration with maximum weight matching. The proposed algorithm addresses the coupled challenges of sequential exploration, matching stability, and function approximation. We prove that the algorithm achieves sublinear regret.

The Best of Both Worlds: Reinforcement Learning with Logarithmic Regret and Policy Switches

In this paper, we study the problem of regret minimization for episodic Reinforcement Learning (RL) both in the model-free and the model-based setting. We focus on learning with general function classes and general model classes, and we derive results that scale with the eluder dimension of these classes. In contrast to the existing body of work that mainly establishes instance-independent regret guarantees, we focus on the instance-dependent setting and show that the regret scales logarithmically with the horizon $T$, provided that there is a gap between the best and the second best action in every state. In addition, we show that such a logarithmic regret bound is realizable by algorithms with $O(\log T)$ switching cost (also known as adaptivity complexity). In other words, these algorithms rarely switch their policy during the course of their execution. Finally, we complement our results with lower bounds which show that even in the tabular setting, we cannot hope for regret guarantees lower than $o(\log T)$.

Learning Dynamic Mechanisms in Unknown Environments: A Reinforcement Learning Approach

Dynamic mechanism design studies how mechanism designers should allocate resources among agents in a time-varying environment. We consider the problem where the agents interact with the mechanism designer according to an unknown Markov Decision Process (MDP), where agent rewards and the mechanism designer's state evolve according to an episodic MDP with unknown reward functions and transition kernels. We focus on the online setting with linear function approximation and attempt to recover the dynamic Vickrey-Clarke-Grove (VCG) mechanism over multiple rounds of interaction. A key contribution of our work is incorporating reward-free online Reinforcement Learning (RL) to aid exploration over a rich policy space to estimate prices in the dynamic VCG mechanism. We show that the regret of our proposed method is upper bounded by $\tilde{\mathcal{O}}(T^{2/3})$ and further devise a lower bound to show that our algorithm is efficient, incurring the same $\tilde{\mathcal{O}}(T^{2 / 3})$ regret as the lower bound, where $T$ is the total number of rounds. Our work establishes the regret guarantee for online RL in solving dynamic mechanism design problems without prior knowledge of the underlying model.

Pessimistic Bootstrapping for Uncertainty-Driven Offline Reinforcement Learning

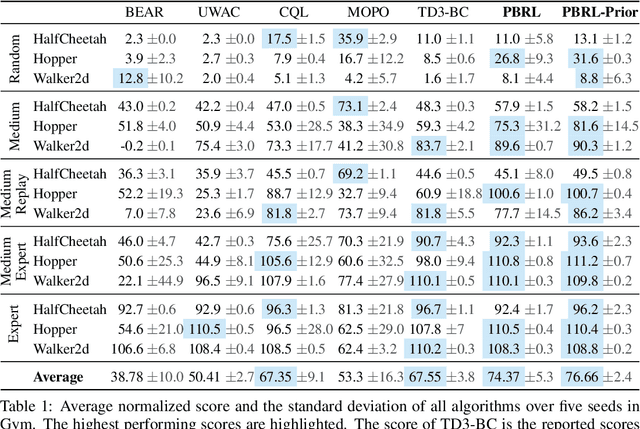
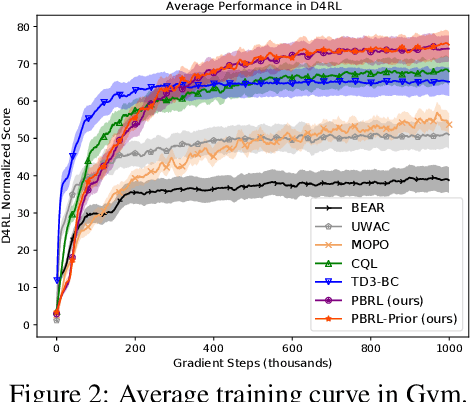
Offline Reinforcement Learning (RL) aims to learn policies from previously collected datasets without exploring the environment. Directly applying off-policy algorithms to offline RL usually fails due to the extrapolation error caused by the out-of-distribution (OOD) actions. Previous methods tackle such problem by penalizing the Q-values of OOD actions or constraining the trained policy to be close to the behavior policy. Nevertheless, such methods typically prevent the generalization of value functions beyond the offline data and also lack precise characterization of OOD data. In this paper, we propose Pessimistic Bootstrapping for offline RL (PBRL), a purely uncertainty-driven offline algorithm without explicit policy constraints. Specifically, PBRL conducts uncertainty quantification via the disagreement of bootstrapped Q-functions, and performs pessimistic updates by penalizing the value function based on the estimated uncertainty. To tackle the extrapolating error, we further propose a novel OOD sampling method. We show that such OOD sampling and pessimistic bootstrapping yields provable uncertainty quantifier in linear MDPs, thus providing the theoretical underpinning for PBRL. Extensive experiments on D4RL benchmark show that PBRL has better performance compared to the state-of-the-art algorithms.

Sequential Information Design: Markov Persuasion Process and Its Efficient Reinforcement Learning

In today's economy, it becomes important for Internet platforms to consider the sequential information design problem to align its long term interest with incentives of the gig service providers. This paper proposes a novel model of sequential information design, namely the Markov persuasion processes (MPPs), where a sender, with informational advantage, seeks to persuade a stream of myopic receivers to take actions that maximizes the sender's cumulative utilities in a finite horizon Markovian environment with varying prior and utility functions. Planning in MPPs thus faces the unique challenge in finding a signaling policy that is simultaneously persuasive to the myopic receivers and inducing the optimal long-term cumulative utilities of the sender. Nevertheless, in the population level where the model is known, it turns out that we can efficiently determine the optimal (resp. $\epsilon$-optimal) policy with finite (resp. infinite) states and outcomes, through a modified formulation of the Bellman equation. Our main technical contribution is to study the MPP under the online reinforcement learning (RL) setting, where the goal is to learn the optimal signaling policy by interacting with with the underlying MPP, without the knowledge of the sender's utility functions, prior distributions, and the Markov transition kernels. We design a provably efficient no-regret learning algorithm, the Optimism-Pessimism Principle for Persuasion Process (OP4), which features a novel combination of both optimism and pessimism principles. Our algorithm enjoys sample efficiency by achieving a sublinear $\sqrt{T}$-regret upper bound. Furthermore, both our algorithm and theory can be applied to MPPs with large space of outcomes and states via function approximation, and we showcase such a success under the linear setting.

Pessimistic Minimax Value Iteration: Provably Efficient Equilibrium Learning from Offline Datasets

We study episodic two-player zero-sum Markov games (MGs) in the offline setting, where the goal is to find an approximate Nash equilibrium (NE) policy pair based on a dataset collected a priori. When the dataset does not have uniform coverage over all policy pairs, finding an approximate NE involves challenges in three aspects: (i) distributional shift between the behavior policy and the optimal policy, (ii) function approximation to handle large state space, and (iii) minimax optimization for equilibrium solving. We propose a pessimism-based algorithm, dubbed as pessimistic minimax value iteration (PMVI), which overcomes the distributional shift by constructing pessimistic estimates of the value functions for both players and outputs a policy pair by solving NEs based on the two value functions. Furthermore, we establish a data-dependent upper bound on the suboptimality which recovers a sublinear rate without the assumption on uniform coverage of the dataset. We also prove an information-theoretical lower bound, which suggests that the data-dependent term in the upper bound is intrinsic. Our theoretical results also highlight a notion of "relative uncertainty", which characterizes the necessary and sufficient condition for achieving sample efficiency in offline MGs. To the best of our knowledge, we provide the first nearly minimax optimal result for offline MGs with function approximation.