Taming Equilibrium Bias in Risk-Sensitive Multi-Agent Reinforcement Learning

We study risk-sensitive multi-agent reinforcement learning under general-sum Markov games, where agents optimize the entropic risk measure of rewards with possibly diverse risk preferences. We show that using the regret naively adapted from existing literature as a performance metric could induce policies with equilibrium bias that favor the most risk-sensitive agents and overlook the other agents. To address such deficiency of the naive regret, we propose a novel notion of regret, which we call risk-balanced regret, and show through a lower bound that it overcomes the issue of equilibrium bias. Furthermore, we develop a self-play algorithm for learning Nash, correlated, and coarse correlated equilibria in risk-sensitive Markov games. We prove that the proposed algorithm attains near-optimal regret guarantees with respect to the risk-balanced regret.

Finding Regularized Competitive Equilibria of Heterogeneous Agent Macroeconomic Models with Reinforcement Learning

We study a heterogeneous agent macroeconomic model with an infinite number of households and firms competing in a labor market. Each household earns income and engages in consumption at each time step while aiming to maximize a concave utility subject to the underlying market conditions. The households aim to find the optimal saving strategy that maximizes their discounted cumulative utility given the market condition, while the firms determine the market conditions through maximizing corporate profit based on the household population behavior. The model captures a wide range of applications in macroeconomic studies, and we propose a data-driven reinforcement learning framework that finds the regularized competitive equilibrium of the model. The proposed algorithm enjoys theoretical guarantees in converging to the equilibrium of the market at a sub-linear rate.

Learn to Match with No Regret: Reinforcement Learning in Markov Matching Markets

We study a Markov matching market involving a planner and a set of strategic agents on the two sides of the market. At each step, the agents are presented with a dynamical context, where the contexts determine the utilities. The planner controls the transition of the contexts to maximize the cumulative social welfare, while the agents aim to find a myopic stable matching at each step. Such a setting captures a range of applications including ridesharing platforms. We formalize the problem by proposing a reinforcement learning framework that integrates optimistic value iteration with maximum weight matching. The proposed algorithm addresses the coupled challenges of sequential exploration, matching stability, and function approximation. We prove that the algorithm achieves sublinear regret.

Cascaded Gaps: Towards Gap-Dependent Regret for Risk-Sensitive Reinforcement Learning

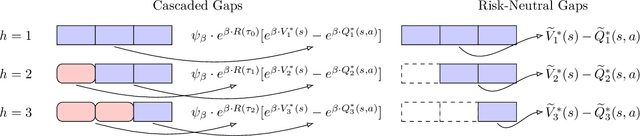
In this paper, we study gap-dependent regret guarantees for risk-sensitive reinforcement learning based on the entropic risk measure. We propose a novel definition of sub-optimality gaps, which we call cascaded gaps, and we discuss their key components that adapt to the underlying structures of the problem. Based on the cascaded gaps, we derive non-asymptotic and logarithmic regret bounds for two model-free algorithms under episodic Markov decision processes. We show that, in appropriate settings, these bounds feature exponential improvement over existing ones that are independent of gaps. We also prove gap-dependent lower bounds, which certify the near optimality of the upper bounds.

Convergence and Alignment of Gradient Descent with Random Back Propagation Weights

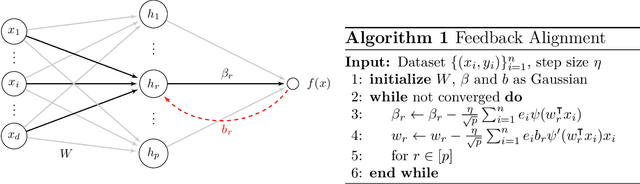
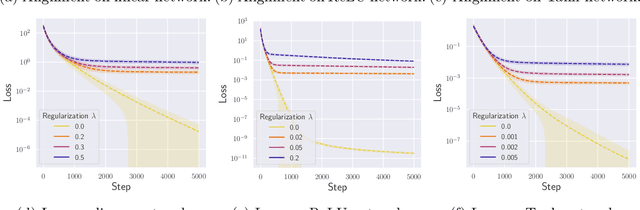
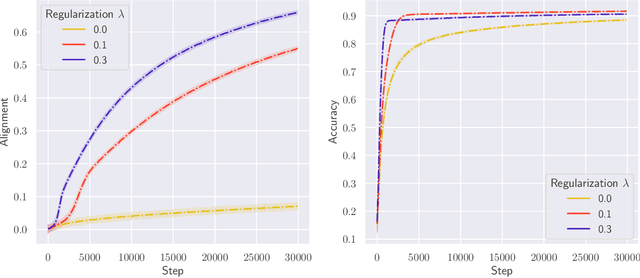
Stochastic gradient descent with backpropagation is the workhorse of artificial neural networks. It has long been recognized that backpropagation fails to be a biologically plausible algorithm. Fundamentally, it is a non-local procedure -- updating one neuron's synaptic weights requires knowledge of synaptic weights or receptive fields of downstream neurons. This limits the use of artificial neural networks as a tool for understanding the biological principles of information processing in the brain. Lillicrap et al. (2016) propose a more biologically plausible "feedback alignment" algorithm that uses random and fixed backpropagation weights, and show promising simulations. In this paper we study the mathematical properties of the feedback alignment procedure by analyzing convergence and alignment for two-layer networks under squared error loss. In the overparameterized setting, we prove that the error converges to zero exponentially fast, and also that regularization is necessary in order for the parameters to become aligned with the random backpropagation weights. Simulations are given that are consistent with this analysis and suggest further generalizations. These results contribute to our understanding of how biologically plausible algorithms might carry out weight learning in a manner different from Hebbian learning, with performance that is comparable with the full non-local backpropagation algorithm.

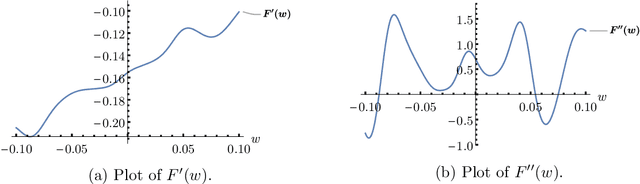
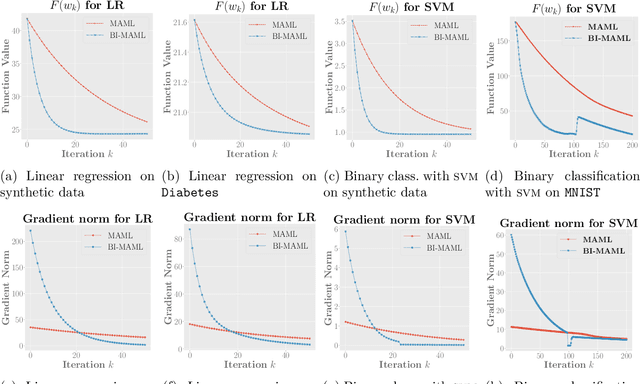
Meta Learning in the Continuous Time Limit

In this paper, we establish the ordinary differential equation (ODE) that underlies the training dynamics of Model-Agnostic Meta-Learning (MAML). Our continuous-time limit view of the process eliminates the influence of the manually chosen step size of gradient descent and includes the existing gradient descent training algorithm as a special case that results from a specific discretization. We show that the MAML ODE enjoys a linear convergence rate to an approximate stationary point of the MAML loss function for strongly convex task losses, even when the corresponding MAML loss is non-convex. Moreover, through the analysis of the MAML ODE, we propose a new BI-MAML training algorithm that significantly reduces the computational burden associated with existing MAML training methods. To complement our theoretical findings, we perform empirical experiments to showcase the superiority of our proposed methods with respect to the existing work.

Learning the Kernel for Classification and Regression

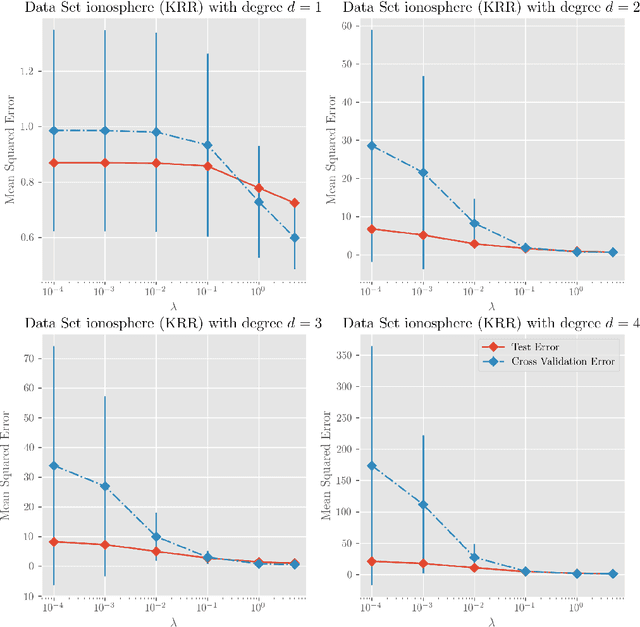
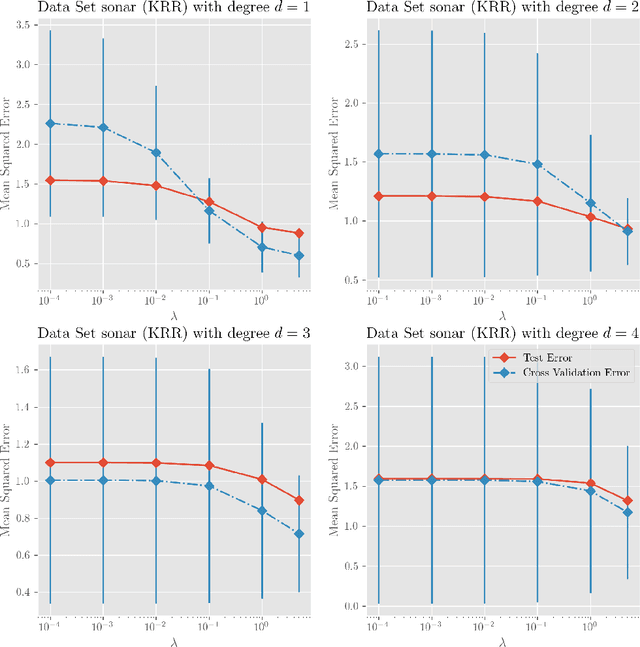
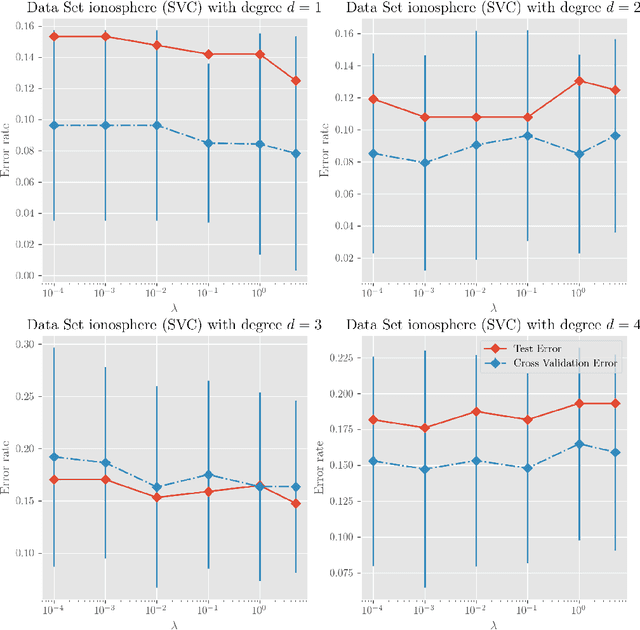
We investigate a series of learning kernel problems with polynomial combinations of base kernels, which will help us solve regression and classification problems. We also perform some numerical experiments of polynomial kernels with regression and classification tasks on different datasets.