Integrating Intermediate Layer Optimization and Projected Gradient Descent for Solving Inverse Problems with Diffusion Models

Inverse problems (IPs) involve reconstructing signals from noisy observations. Recently, diffusion models (DMs) have emerged as a powerful framework for solving IPs, achieving remarkable reconstruction performance. However, existing DM-based methods frequently encounter issues such as heavy computational demands and suboptimal convergence. In this work, building upon the idea of the recent work DMPlug, we propose two novel methods, DMILO and DMILO-PGD, to address these challenges. Our first method, DMILO, employs intermediate layer optimization (ILO) to alleviate the memory burden inherent in DMPlug. Additionally, by introducing sparse deviations, we expand the range of DMs, enabling the exploration of underlying signals that may lie outside the range of the diffusion model. We further propose DMILO-PGD, which integrates ILO with projected gradient descent (PGD), thereby reducing the risk of suboptimal convergence. We provide an intuitive theoretical analysis of our approaches under appropriate conditions and validate their superiority through extensive experiments on diverse image datasets, encompassing both linear and nonlinear IPs. Our results demonstrate significant performance gains over state-of-the-art methods, highlighting the effectiveness of DMILO and DMILO-PGD in addressing common challenges in DM-based IP solvers.

Learning Single Index Models with Diffusion Priors

Diffusion models (DMs) have demonstrated remarkable ability to generate diverse and high-quality images by efficiently modeling complex data distributions. They have also been explored as powerful generative priors for signal recovery, resulting in a substantial improvement in the quality of reconstructed signals. However, existing research on signal recovery with diffusion models either focuses on specific reconstruction problems or is unable to handle nonlinear measurement models with discontinuous or unknown link functions. In this work, we focus on using DMs to achieve accurate recovery from semi-parametric single index models, which encompass a variety of popular nonlinear models that may have {\em discontinuous} and {\em unknown} link functions. We propose an efficient reconstruction method that only requires one round of unconditional sampling and (partial) inversion of DMs. Theoretical analysis on the effectiveness of the proposed methods has been established under appropriate conditions. We perform numerical experiments on image datasets for different nonlinear measurement models. We observe that compared to competing methods, our approach can yield more accurate reconstructions while utilizing significantly fewer neural function evaluations.

Generalized Eigenvalue Problems with Generative Priors

Generalized eigenvalue problems (GEPs) find applications in various fields of science and engineering. For example, principal component analysis, Fisher's discriminant analysis, and canonical correlation analysis are specific instances of GEPs and are widely used in statistical data processing. In this work, we study GEPs under generative priors, assuming that the underlying leading generalized eigenvector lies within the range of a Lipschitz continuous generative model. Under appropriate conditions, we show that any optimal solution to the corresponding optimization problems attains the optimal statistical rate. Moreover, from a computational perspective, we propose an iterative algorithm called the Projected Rayleigh Flow Method (PRFM) to approximate the optimal solution. We theoretically demonstrate that under suitable assumptions, PRFM converges linearly to an estimated vector that achieves the optimal statistical rate. Numerical results are provided to demonstrate the effectiveness of the proposed method.

Robust Instance Optimal Phase-Only Compressed Sensing

Phase-only compressed sensing (PO-CS) is concerned with the recovery of structured signals from the phases of complex measurements. Recent results show that structured signals in the standard sphere $\mathbb{S}^{n-1}$ can be exactly recovered from complex Gaussian phases, by recasting PO-CS as linear compressed sensing and then applying existing solvers such as basis pursuit. Known guarantees are either non-uniform or do not tolerate model error. We show that this linearization approach is more powerful than the prior results indicate. First, it achieves uniform instance optimality: Under complex Gaussian matrix with a near-optimal number of rows, this approach uniformly recovers all signals in $\mathbb{S}^{n-1}$ with errors proportional to the model errors of the signals. Specifically, for sparse recovery there exists an efficient estimator $\mathbf{x}^\sharp$ and some universal constant $C$ such that $\|\mathbf{x}^\sharp-\mathbf{x}\|_2\le \frac{C\sigma_s(\mathbf{x})_1}{\sqrt{s}}~(\forall\mathbf{x}\in\mathbb{S}^{n-1})$, where $\sigma_s(\mathbf{x})_1=\min_{\mathbf{u}\in\Sigma^n_s}\|\mathbf{u}-\mathbf{x}\|_1$ is the model error under $\ell_1$-norm. Second, the instance optimality is robust to small dense disturbances and sparse corruptions that arise before or after capturing the phases. As an extension, we also propose to recast sparsely corrupted PO-CS as a linear corrupted sensing problem and show that this achieves perfect reconstruction of the signals. Our results resemble the instance optimal guarantees in linear compressed sensing and, to our knowledge, are the first results of this kind for a non-linear sensing scenario.

Accelerating Diffusion Sampling with Optimized Time Steps

Diffusion probabilistic models (DPMs) have shown remarkable performance in high-resolution image synthesis, but their sampling efficiency is still to be desired due to the typically large number of sampling steps. Recent advancements in high-order numerical ODE solvers for DPMs have enabled the generation of high-quality images with much fewer sampling steps. While this is a significant development, most sampling methods still employ uniform time steps, which is not optimal when using a small number of steps. To address this issue, we propose a general framework for designing an optimization problem that seeks more appropriate time steps for a specific numerical ODE solver for DPMs. This optimization problem aims to minimize the distance between the ground-truth solution to the ODE and an approximate solution corresponding to the numerical solver. It can be efficiently solved using the constrained trust region method, taking less than $15$ seconds. Our extensive experiments on both unconditional and conditional sampling using pixel- and latent-space DPMs demonstrate that, when combined with the state-of-the-art sampling method UniPC, our optimized time steps significantly improve image generation performance in terms of FID scores for datasets such as CIFAR-10 and ImageNet, compared to using uniform time steps.

The Surprising Effectiveness of Skip-Tuning in Diffusion Sampling

With the incorporation of the UNet architecture, diffusion probabilistic models have become a dominant force in image generation tasks. One key design in UNet is the skip connections between the encoder and decoder blocks. Although skip connections have been shown to improve training stability and model performance, we reveal that such shortcuts can be a limiting factor for the complexity of the transformation. As the sampling steps decrease, the generation process and the role of the UNet get closer to the push-forward transformations from Gaussian distribution to the target, posing a challenge for the network's complexity. To address this challenge, we propose Skip-Tuning, a simple yet surprisingly effective training-free tuning method on the skip connections. Our method can achieve 100% FID improvement for pretrained EDM on ImageNet 64 with only 19 NFEs (1.75), breaking the limit of ODE samplers regardless of sampling steps. Surprisingly, the improvement persists when we increase the number of sampling steps and can even surpass the best result from EDM-2 (1.58) with only 39 NFEs (1.57). Comprehensive exploratory experiments are conducted to shed light on the surprising effectiveness. We observe that while Skip-Tuning increases the score-matching losses in the pixel space, the losses in the feature space are reduced, particularly at intermediate noise levels, which coincide with the most effective range accounting for image quality improvement.

On the Expressive Power of a Variant of the Looped Transformer

Besides natural language processing, transformers exhibit extraordinary performance in solving broader applications, including scientific computing and computer vision. Previous works try to explain this from the expressive power and capability perspectives that standard transformers are capable of performing some algorithms. To empower transformers with algorithmic capabilities and motivated by the recently proposed looped transformer (Yang et al., 2024; Giannou et al., 2023), we design a novel transformer block, dubbed Algorithm Transformer (abbreviated as AlgoFormer). Compared with the standard transformer and vanilla looped transformer, the proposed AlgoFormer can achieve significantly higher expressiveness in algorithm representation when using the same number of parameters. In particular, inspired by the structure of human-designed learning algorithms, our transformer block consists of a pre-transformer that is responsible for task pre-processing, a looped transformer for iterative optimization algorithms, and a post-transformer for producing the desired results after post-processing. We provide theoretical evidence of the expressive power of the AlgoFormer in solving some challenging problems, mirroring human-designed algorithms. Furthermore, some theoretical and empirical results are presented to show that the designed transformer has the potential to be smarter than human-designed algorithms. Experimental results demonstrate the empirical superiority of the proposed transformer in that it outperforms the standard transformer and vanilla looped transformer in some challenging tasks.

Uniform Recovery Guarantees for Quantized Corrupted Sensing Using Structured or Generative Priors

This paper studies quantized corrupted sensing where the measurements are contaminated by unknown corruption and then quantized by a dithered uniform quantizer. We establish uniform guarantees for Lasso that ensure the accurate recovery of all signals and corruptions using a single draw of the sub-Gaussian sensing matrix and uniform dither. For signal and corruption with structured priors (e.g., sparsity, low-rankness), our uniform error rate for constrained Lasso typically coincides with the non-uniform one [Sun, Cui and Liu, 2022] up to logarithmic factors. By contrast, our uniform error rate for unconstrained Lasso exhibits worse dependence on the structured parameters due to regularization parameters larger than the ones for non-uniform recovery. For signal and corruption living in the ranges of some Lipschitz continuous generative models (referred to as generative priors), we achieve uniform recovery via constrained Lasso with a measurement number proportional to the latent dimensions of the generative models. Our treatments to the two kinds of priors are (nearly) unified and share the common key ingredients of (global) quantized product embedding (QPE) property, which states that the dithered uniform quantization (universally) preserves inner product. As a by-product, our QPE result refines the one in [Xu and Jacques, 2020] under sub-Gaussian random matrix, and in this specific instance we are able to sharpen the uniform error decaying rate (for the projected-back projection estimator with signals in some convex symmetric set) presented therein from $O(m^{-1/16})$ to $O(m^{-1/8})$.

Solving Quadratic Systems with Full-Rank Matrices Using Sparse or Generative Priors

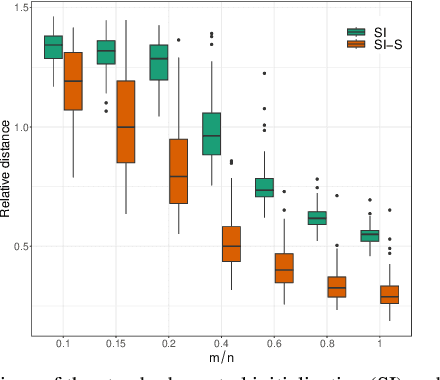
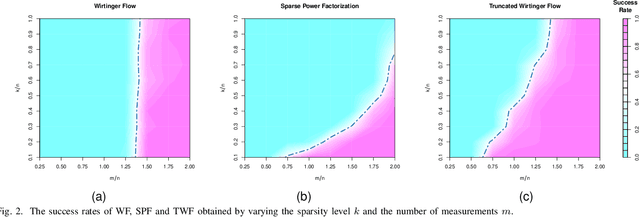
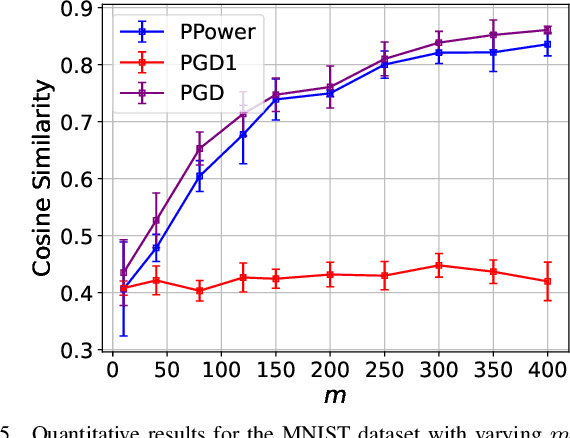
The problem of recovering a signal $\boldsymbol{x} \in \mathbb{R}^n$ from a quadratic system $\{y_i=\boldsymbol{x}^\top\boldsymbol{A}_i\boldsymbol{x},\ i=1,\ldots,m\}$ with full-rank matrices $\boldsymbol{A}_i$ frequently arises in applications such as unassigned distance geometry and sub-wavelength imaging. With i.i.d. standard Gaussian matrices $\boldsymbol{A}_i$, this paper addresses the high-dimensional case where $m\ll n$ by incorporating prior knowledge of $\boldsymbol{x}$. First, we consider a $k$-sparse $\boldsymbol{x}$ and introduce the thresholded Wirtinger flow (TWF) algorithm that does not require the sparsity level $k$. TWF comprises two steps: the spectral initialization that identifies a point sufficiently close to $\boldsymbol{x}$ (up to a sign flip) when $m=O(k^2\log n)$, and the thresholded gradient descent (with a good initialization) that produces a sequence linearly converging to $\boldsymbol{x}$ with $m=O(k\log n)$ measurements. Second, we explore the generative prior, assuming that $\boldsymbol{x}$ lies in the range of an $L$-Lipschitz continuous generative model with $k$-dimensional inputs in an $\ell_2$-ball of radius $r$. We develop the projected gradient descent (PGD) algorithm that also comprises two steps: the projected power method that provides an initial vector with $O\big(\sqrt{\frac{k \log L}{m}}\big)$ $\ell_2$-error given $m=O(k\log(Lnr))$ measurements, and the projected gradient descent that refines the $\ell_2$-error to $O(\delta)$ at a geometric rate when $m=O(k\log\frac{Lrn}{\delta^2})$. Experimental results corroborate our theoretical findings and show that: (i) our approach for the sparse case notably outperforms the existing provable algorithm sparse power factorization; (ii) leveraging the generative prior allows for precise image recovery in the MNIST dataset from a small number of quadratic measurements.

DiffFit: Unlocking Transferability of Large Diffusion Models via Simple Parameter-Efficient Fine-Tuning

Diffusion models have proven to be highly effective in generating high-quality images. However, adapting large pre-trained diffusion models to new domains remains an open challenge, which is critical for real-world applications. This paper proposes DiffFit, a parameter-efficient strategy to fine-tune large pre-trained diffusion models that enable fast adaptation to new domains. DiffFit is embarrassingly simple that only fine-tunes the bias term and newly-added scaling factors in specific layers, yet resulting in significant training speed-up and reduced model storage costs. Compared with full fine-tuning, DiffFit achieves 2$\times$ training speed-up and only needs to store approximately 0.12\% of the total model parameters. Intuitive theoretical analysis has been provided to justify the efficacy of scaling factors on fast adaptation. On 8 downstream datasets, DiffFit achieves superior or competitive performances compared to the full fine-tuning while being more efficient. Remarkably, we show that DiffFit can adapt a pre-trained low-resolution generative model to a high-resolution one by adding minimal cost. Among diffusion-based methods, DiffFit sets a new state-of-the-art FID of 3.02 on ImageNet 512$\times$512 benchmark by fine-tuning only 25 epochs from a public pre-trained ImageNet 256$\times$256 checkpoint while being 30$\times$ more training efficient than the closest competitor.