Follow-Your-Shape: Shape-Aware Image Editing via Trajectory-Guided Region Control

While recent flow-based image editing models demonstrate general-purpose capabilities across diverse tasks, they often struggle to specialize in challenging scenarios -- particularly those involving large-scale shape transformations. When performing such structural edits, these methods either fail to achieve the intended shape change or inadvertently alter non-target regions, resulting in degraded background quality. We propose Follow-Your-Shape, a training-free and mask-free framework that supports precise and controllable editing of object shapes while strictly preserving non-target content. Motivated by the divergence between inversion and editing trajectories, we compute a Trajectory Divergence Map (TDM) by comparing token-wise velocity differences between the inversion and denoising paths. The TDM enables precise localization of editable regions and guides a Scheduled KV Injection mechanism that ensures stable and faithful editing. To facilitate a rigorous evaluation, we introduce ReShapeBench, a new benchmark comprising 120 new images and enriched prompt pairs specifically curated for shape-aware editing. Experiments demonstrate that our method achieves superior editability and visual fidelity, particularly in tasks requiring large-scale shape replacement.

Follow-Your-Instruction: A Comprehensive MLLM Agent for World Data Synthesis

With the growing demands of AI-generated content (AIGC), the need for high-quality, diverse, and scalable data has become increasingly crucial. However, collecting large-scale real-world data remains costly and time-consuming, hindering the development of downstream applications. While some works attempt to collect task-specific data via a rendering process, most approaches still rely on manual scene construction, limiting their scalability and accuracy. To address these challenges, we propose Follow-Your-Instruction, a Multimodal Large Language Model (MLLM)-driven framework for automatically synthesizing high-quality 2D, 3D, and 4D data. Our \textbf{Follow-Your-Instruction} first collects assets and their associated descriptions through multimodal inputs using the MLLM-Collector. Then it constructs 3D layouts, and leverages Vision-Language Models (VLMs) for semantic refinement through multi-view scenes with the MLLM-Generator and MLLM-Optimizer, respectively. Finally, it uses MLLM-Planner to generate temporally coherent future frames. We evaluate the quality of the generated data through comprehensive experiments on the 2D, 3D, and 4D generative tasks. The results show that our synthetic data significantly boosts the performance of existing baseline models, demonstrating Follow-Your-Instruction's potential as a scalable and effective data engine for generative intelligence.

Follow-Your-Motion: Video Motion Transfer via Efficient Spatial-Temporal Decoupled Finetuning

Recently, breakthroughs in the video diffusion transformer have shown remarkable capabilities in diverse motion generations. As for the motion-transfer task, current methods mainly use two-stage Low-Rank Adaptations (LoRAs) finetuning to obtain better performance. However, existing adaptation-based motion transfer still suffers from motion inconsistency and tuning inefficiency when applied to large video diffusion transformers. Naive two-stage LoRA tuning struggles to maintain motion consistency between generated and input videos due to the inherent spatial-temporal coupling in the 3D attention operator. Additionally, they require time-consuming fine-tuning processes in both stages. To tackle these issues, we propose Follow-Your-Motion, an efficient two-stage video motion transfer framework that finetunes a powerful video diffusion transformer to synthesize complex motion.Specifically, we propose a spatial-temporal decoupled LoRA to decouple the attention architecture for spatial appearance and temporal motion processing. During the second training stage, we design the sparse motion sampling and adaptive RoPE to accelerate the tuning speed. To address the lack of a benchmark for this field, we introduce MotionBench, a comprehensive benchmark comprising diverse motion, including creative camera motion, single object motion, multiple object motion, and complex human motion. We show extensive evaluations on MotionBench to verify the superiority of Follow-Your-Motion.

Follow-Your-Creation: Empowering 4D Creation through Video Inpainting

We introduce Follow-Your-Creation, a novel 4D video creation framework capable of both generating and editing 4D content from a single monocular video input. By leveraging a powerful video inpainting foundation model as a generative prior, we reformulate 4D video creation as a video inpainting task, enabling the model to fill in missing content caused by camera trajectory changes or user edits. To facilitate this, we generate composite masked inpainting video data to effectively fine-tune the model for 4D video generation. Given an input video and its associated camera trajectory, we first perform depth-based point cloud rendering to obtain invisibility masks that indicate the regions that should be completed. Simultaneously, editing masks are introduced to specify user-defined modifications, and these are combined with the invisibility masks to create a composite masks dataset. During training, we randomly sample different types of masks to construct diverse and challenging inpainting scenarios, enhancing the model's generalization and robustness in various 4D editing and generation tasks. To handle temporal consistency under large camera motion, we design a self-iterative tuning strategy that gradually increases the viewing angles during training, where the model is used to generate the next-stage training data after each fine-tuning iteration. Moreover, we introduce a temporal packaging module during inference to enhance generation quality. Our method effectively leverages the prior knowledge of the base model without degrading its original performance, enabling the generation of 4D videos with consistent multi-view coherence. In addition, our approach supports prompt-based content editing, demonstrating strong flexibility and significantly outperforming state-of-the-art methods in both quality and versatility.

Language Model Distillation: A Temporal Difference Imitation Learning Perspective

Large language models have led to significant progress across many NLP tasks, although their massive sizes often incur substantial computational costs. Distillation has become a common practice to compress these large and highly capable models into smaller, more efficient ones. Many existing language model distillation methods can be viewed as behavior cloning from the perspective of imitation learning or inverse reinforcement learning. This viewpoint has inspired subsequent studies that leverage (inverse) reinforcement learning techniques, including variations of behavior cloning and temporal difference learning methods. Rather than proposing yet another specific temporal difference method, we introduce a general framework for temporal difference-based distillation by exploiting the distributional sparsity of the teacher model. Specifically, it is often observed that language models assign most probability mass to a small subset of tokens. Motivated by this observation, we design a temporal difference learning framework that operates on a reduced action space (a subset of vocabulary), and demonstrate how practical algorithms can be derived and the resulting performance improvements.

Fairness Risks for Group-conditionally Missing Demographics

Fairness-aware classification models have gained increasing attention in recent years as concerns grow on discrimination against some demographic groups. Most existing models require full knowledge of the sensitive features, which can be impractical due to privacy, legal issues, and an individual's fear of discrimination. The key challenge we will address is the group dependency of the unavailability, e.g., people of some age range may be more reluctant to reveal their age. Our solution augments general fairness risks with probabilistic imputations of the sensitive features, while jointly learning the group-conditionally missing probabilities in a variational auto-encoder. Our model is demonstrated effective on both image and tabular datasets, achieving an improved balance between accuracy and fairness.

Distilling Conditional Diffusion Models for Offline Reinforcement Learning through Trajectory Stitching

Deep generative models have recently emerged as an effective approach to offline reinforcement learning. However, their large model size poses challenges in computation. We address this issue by proposing a knowledge distillation method based on data augmentation. In particular, high-return trajectories are generated from a conditional diffusion model, and they are blended with the original trajectories through a novel stitching algorithm that leverages a new reward generator. Applying the resulting dataset to behavioral cloning, the learned shallow policy whose size is much smaller outperforms or nearly matches deep generative planners on several D4RL benchmarks.

Machine Learning for Detection of 3D Features using sparse X-ray data

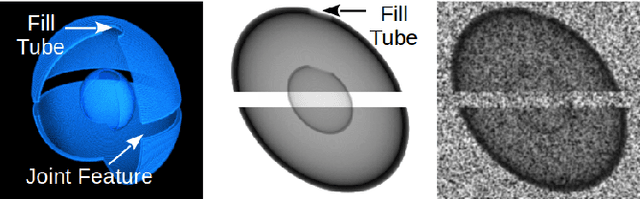
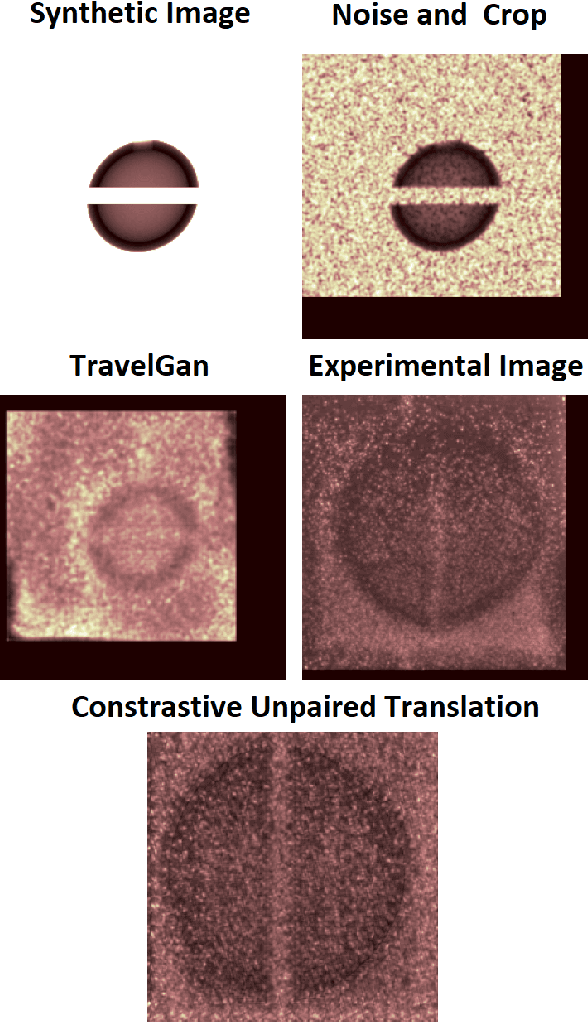
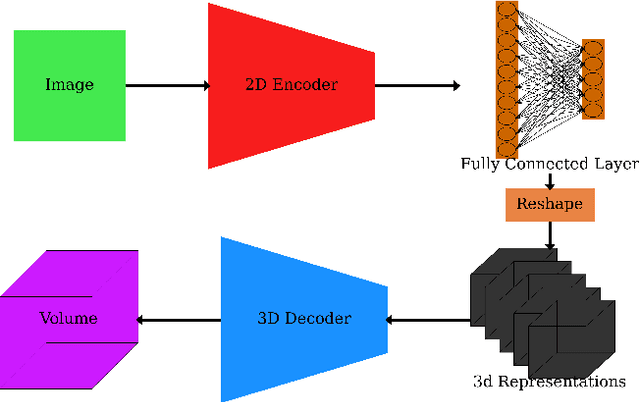
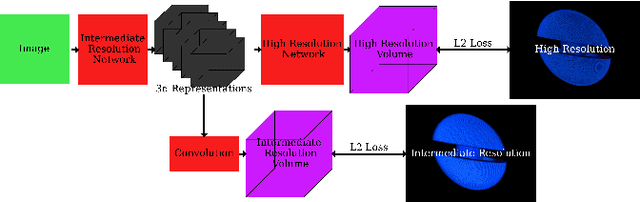
In many inertial confinement fusion experiments, the neutron yield and other parameters cannot be completely accounted for with one and two dimensional models. This discrepancy suggests that there are three dimensional effects which may be significant. Sources of these effects include defects in the shells and shell interfaces, the fill tube of the capsule, and the joint feature in double shell targets. Due to their ability to penetrate materials, X-rays are used to capture the internal structure of objects. Methods such as Computational Tomography use X-ray radiographs from hundreds of projections in order to reconstruct a three dimensional model of the object. In experimental environments, such as the National Ignition Facility and Omega-60, the availability of these views is scarce and in many cases only consist of a single line of sight. Mathematical reconstruction of a 3D object from sparse views is an ill-posed inverse problem. These types of problems are typically solved by utilizing prior information. Neural networks have been used for the task of 3D reconstruction as they are capable of encoding and leveraging this prior information. We utilize half a dozen different convolutional neural networks to produce different 3D representations of ICF implosions from the experimental data. We utilize deep supervision to train a neural network to produce high resolution reconstructions. We use these representations to track 3D features of the capsules such as the ablator, inner shell, and the joint between shell hemispheres. Machine learning, supplemented by different priors, is a promising method for 3D reconstructions in ICF and X-ray radiography in general.

Orthogonal Gromov-Wasserstein Discrepancy with Efficient Lower Bound

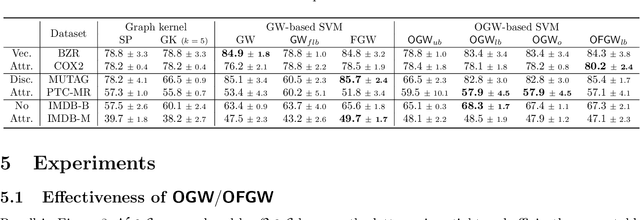
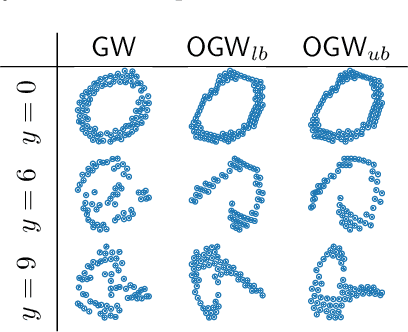
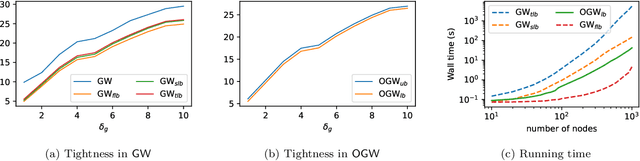
Comparing structured data from possibly different metric-measure spaces is a fundamental task in machine learning, with applications in, e.g., graph classification. The Gromov-Wasserstein (GW) discrepancy formulates a coupling between the structured data based on optimal transportation, tackling the incomparability between different structures by aligning the intra-relational geometries. Although efficient local solvers such as conditional gradient and Sinkhorn are available, the inherent non-convexity still prevents a tractable evaluation, and the existing lower bounds are not tight enough for practical use. To address this issue, we take inspiration from the connection with the quadratic assignment problem, and propose the orthogonal Gromov-Wasserstein (OGW) discrepancy as a surrogate of GW. It admits an efficient and closed-form lower bound with the complexity of $\mathcal{O}(n^3)$, and directly extends to the fused Gromov-Wasserstein (FGW) distance, incorporating node features into the coupling. Extensive experiments on both the synthetic and real-world datasets show the tightness of our lower bounds, and both OGW and its lower bounds efficiently deliver accurate predictions and satisfactory barycenters for graph sets.

Similarity Equivariant Linear Transformation of Joint Orientation-Scale Space Representations

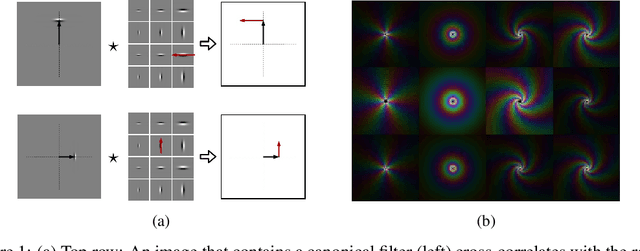
Convolution is conventionally defined as a linear operation on functions of one or more variables which commutes with shifts. Group convolution generalizes the concept to linear operations on functions of group elements representing more general geometric transformations and which commute with those transformations. Since similarity transformation is the most general geometric transformation on images that preserves shape, the group convolution that is equivariant to similarity transformation is the most general shape preserving linear operator. Because similarity transformations have four free parameters, group convolutions are defined on four-dimensional, joint orientation-scale spaces. Although prior work on equivariant linear operators has been limited to discrete groups, the similarity group is continuous. In this paper, we describe linear operators on discrete representations that are equivariant to continuous similarity transformation. This is achieved by using a basis of functions that is it joint shiftable-twistable-scalable. These pinwheel functions use Fourier series in the orientation dimension and Laplace transform in the log-scale dimension to form a basis of spatially localized functions that can be continuously interpolated in position, orientation and scale. Although this result is potentially significant with respect to visual computation generally, we present an initial demonstration of its utility by using it to compute a shape equivariant distribution of closed contours traced by particles undergoing Brownian motion in velocity. The contours are constrained by sets of points and line endings representing well known bistable illusory contour inducing patterns.