Graph Neural Network-Enhanced Expectation Propagation Algorithm for MIMO Turbo Receivers

Deep neural networks (NNs) are considered a powerful tool for balancing the performance and complexity of multiple-input multiple-output (MIMO) receivers due to their accurate feature extraction, high parallelism, and excellent inference ability. Graph NNs (GNNs) have recently demonstrated outstanding capability in learning enhanced message passing rules and have shown success in overcoming the drawback of inaccurate Gaussian approximation of expectation propagation (EP)-based MIMO detectors. However, the application of the GNN-enhanced EP detector to MIMO turbo receivers is underexplored and non-trivial due to the requirement of extrinsic information for iterative processing. This paper proposes a GNN-enhanced EP algorithm for MIMO turbo receivers, which realizes the turbo principle of generating extrinsic information from the MIMO detector through a specially designed training procedure. Additionally, an edge pruning strategy is designed to eliminate redundant connections in the original fully connected model of the GNN utilizing the correlation information inherently from the EP algorithm. Edge pruning reduces the computational cost dramatically and enables the network to focus more attention on the weights that are vital for performance. Simulation results and complexity analysis indicate that the proposed MIMO turbo receiver outperforms the EP turbo approaches by over 1 dB at the bit error rate of $10^{-5}$, exhibits performance equivalent to state-of-the-art receivers with 2.5 times shorter running time, and adapts to various scenarios.

Gradient-Based Markov Chain Monte Carlo for MIMO Detection

Accurately detecting symbols transmitted over multiple-input multiple-output (MIMO) wireless channels is crucial in realizing the benefits of MIMO techniques. However, optimal MIMO detection is associated with a complexity that grows exponentially with the MIMO dimensions and quickly becomes impractical. Recently, stochastic sampling-based Bayesian inference techniques, such as Markov chain Monte Carlo (MCMC), have been combined with the gradient descent (GD) method to provide a promising framework for MIMO detection. In this work, we propose to efficiently approach optimal detection by exploring the discrete search space via MCMC random walk accelerated by Nesterov's gradient method. Nesterov's GD guides MCMC to make efficient searches without the computationally expensive matrix inversion and line search. Our proposed method operates using multiple GDs per random walk, achieving sufficient descent towards important regions of the search space before adding random perturbations, guaranteeing high sampling efficiency. To provide augmented exploration, extra samples are derived through the trajectory of Nesterov's GD by simple operations, effectively supplementing the sample list for statistical inference and boosting the overall MIMO detection performance. Furthermore, we design an early stopping tactic to terminate unnecessary further searches, remarkably reducing the complexity. Simulation results and complexity analysis reveal that the proposed method achieves near-optimal performance in both uncoded and coded MIMO systems, adapts to realistic channel models, and scales well to large MIMO dimensions.

Understanding the Role of Feedback in Online Learning with Switching Costs

In this paper, we study the role of feedback in online learning with switching costs. It has been shown that the minimax regret is $\widetilde{\Theta}(T^{2/3})$ under bandit feedback and improves to $\widetilde{\Theta}(\sqrt{T})$ under full-information feedback, where $T$ is the length of the time horizon. However, it remains largely unknown how the amount and type of feedback generally impact regret. To this end, we first consider the setting of bandit learning with extra observations; that is, in addition to the typical bandit feedback, the learner can freely make a total of $B_{\mathrm{ex}}$ extra observations. We fully characterize the minimax regret in this setting, which exhibits an interesting phase-transition phenomenon: when $B_{\mathrm{ex}} = O(T^{2/3})$, the regret remains $\widetilde{\Theta}(T^{2/3})$, but when $B_{\mathrm{ex}} = \Omega(T^{2/3})$, it becomes $\widetilde{\Theta}(T/\sqrt{B_{\mathrm{ex}}})$, which improves as the budget $B_{\mathrm{ex}}$ increases. To design algorithms that can achieve the minimax regret, it is instructive to consider a more general setting where the learner has a budget of $B$ total observations. We fully characterize the minimax regret in this setting as well and show that it is $\widetilde{\Theta}(T/\sqrt{B})$, which scales smoothly with the total budget $B$. Furthermore, we propose a generic algorithmic framework, which enables us to design different learning algorithms that can achieve matching upper bounds for both settings based on the amount and type of feedback. One interesting finding is that while bandit feedback can still guarantee optimal regret when the budget is relatively limited, it no longer suffices to achieve optimal regret when the budget is relatively large.

Differentially Private Episodic Reinforcement Learning with Heavy-tailed Rewards

In this paper, we study the problem of (finite horizon tabular) Markov decision processes (MDPs) with heavy-tailed rewards under the constraint of differential privacy (DP). Compared with the previous studies for private reinforcement learning that typically assume rewards are sampled from some bounded or sub-Gaussian distributions to ensure DP, we consider the setting where reward distributions have only finite $(1+v)$-th moments with some $v \in (0,1]$. By resorting to robust mean estimators for rewards, we first propose two frameworks for heavy-tailed MDPs, i.e., one is for value iteration and another is for policy optimization. Under each framework, we consider both joint differential privacy (JDP) and local differential privacy (LDP) models. Based on our frameworks, we provide regret upper bounds for both JDP and LDP cases and show that the moment of distribution and privacy budget both have significant impacts on regrets. Finally, we establish a lower bound of regret minimization for heavy-tailed MDPs in JDP model by reducing it to the instance-independent lower bound of heavy-tailed multi-armed bandits in DP model. We also show the lower bound for the problem in LDP by adopting some private minimax methods. Our results reveal that there are fundamental differences between the problem of private RL with sub-Gaussian and that with heavy-tailed rewards.

Provably Efficient Model-Free Algorithms for Non-stationary CMDPs

We study model-free reinforcement learning (RL) algorithms in episodic non-stationary constrained Markov Decision Processes (CMDPs), in which an agent aims to maximize the expected cumulative reward subject to a cumulative constraint on the expected utility (cost). In the non-stationary environment, reward, utility functions, and transition kernels can vary arbitrarily over time as long as the cumulative variations do not exceed certain variation budgets. We propose the first model-free, simulator-free RL algorithms with sublinear regret and zero constraint violation for non-stationary CMDPs in both tabular and linear function approximation settings with provable performance guarantees. Our results on regret bound and constraint violation for the tabular case match the corresponding best results for stationary CMDPs when the total budget is known. Additionally, we present a general framework for addressing the well-known challenges associated with analyzing non-stationary CMDPs, without requiring prior knowledge of the variation budget. We apply the approach for both tabular and linear approximation settings.

On Differentially Private Federated Linear Contextual Bandits

We consider cross-silo federated linear contextual bandit (LCB) problem under differential privacy. In this setting, multiple silos or agents interact with the local users and communicate via a central server to realize collaboration while without sacrificing each user's privacy. We identify two issues in the state-of-the-art algorithm of \cite{dubey2020differentially}: (i) failure of claimed privacy protection and (ii) noise miscalculation in regret bound. To resolve these issues, we take a two-step principled approach. First, we design an algorithmic framework consisting of a generic federated LCB algorithm and flexible privacy protocols. Then, leveraging the proposed framework, we study federated LCBs under two different privacy constraints. We first establish privacy and regret guarantees under silo-level local differential privacy, which fix the issues present in state-of-the-art algorithm. To further improve the regret performance, we next consider shuffle model of differential privacy, under which we show that our algorithm can achieve nearly ``optimal'' regret without a trusted server. We accomplish this via two different schemes -- one relies on a new result on privacy amplification via shuffling for DP mechanisms and another one leverages the integration of a shuffle protocol for vector sum into the tree-based mechanism, both of which might be of independent interest. Finally, we support our theoretical results with numerical evaluations over contextual bandit instances generated from both synthetic and real-life data.

(Private) Kernelized Bandits with Distributed Biased Feedback

In this paper, we study kernelized bandits with distributed biased feedback. This problem is motivated by several real-world applications (such as dynamic pricing, cellular network configuration, and policy making), where users from a large population contribute to the reward of the action chosen by a central entity, but it is difficult to collect feedback from all users. Instead, only biased feedback (due to user heterogeneity) from a subset of users may be available. In addition to such partial biased feedback, we are also faced with two practical challenges due to communication cost and computation complexity. To tackle these challenges, we carefully design a new \emph{distributed phase-then-batch-based elimination (\texttt{DPBE})} algorithm, which samples users in phases for collecting feedback to reduce the bias and employs \emph{maximum variance reduction} to select actions in batches within each phase. By properly choosing the phase length, the batch size, and the confidence width used for eliminating suboptimal actions, we show that \texttt{DPBE} achieves a sublinear regret of $\tilde{O}(T^{1-\alpha/2}+\sqrt{\gamma_T T})$, where $\alpha\in (0,1)$ is the user-sampling parameter one can tune. Moreover, \texttt{DPBE} can significantly reduce both communication cost and computation complexity in distributed kernelized bandits, compared to some variants of the state-of-the-art algorithms (originally developed for standard kernelized bandits). Furthermore, by incorporating various \emph{differential privacy} models (including the central, local, and shuffle models), we generalize \texttt{DPBE} to provide privacy guarantees for users participating in the distributed learning process. Finally, we conduct extensive simulations to validate our theoretical results and evaluate the empirical performance.

On Private and Robust Bandits

We study private and robust multi-armed bandits (MABs), where the agent receives Huber's contaminated heavy-tailed rewards and meanwhile needs to ensure differential privacy. We first present its minimax lower bound, characterizing the information-theoretic limit of regret with respect to privacy budget, contamination level and heavy-tailedness. Then, we propose a meta-algorithm that builds on a private and robust mean estimation sub-routine \texttt{PRM} that essentially relies on reward truncation and the Laplace mechanism only. For two different heavy-tailed settings, we give specific schemes of \texttt{PRM}, which enable us to achieve nearly-optimal regret. As by-products of our main results, we also give the first minimax lower bound for private heavy-tailed MABs (i.e., without contamination). Moreover, our two proposed truncation-based \texttt{PRM} achieve the optimal trade-off between estimation accuracy, privacy and robustness. Finally, we support our theoretical results with experimental studies.

Grant-Free NOMA-OTFS Paradigm: Enabling Efficient Ubiquitous Access for LEO Satellite Internet-of-Things

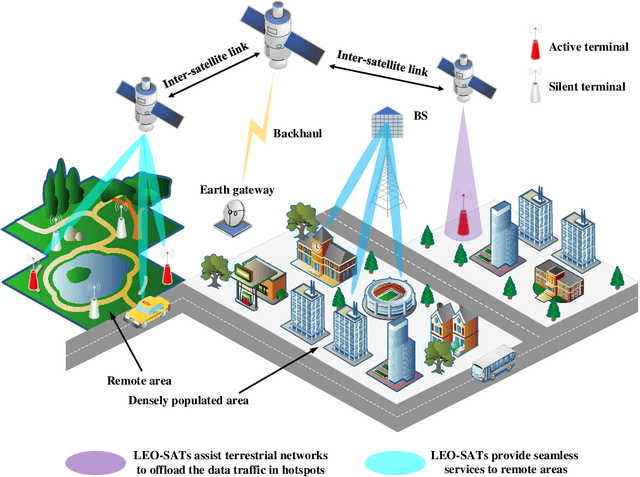
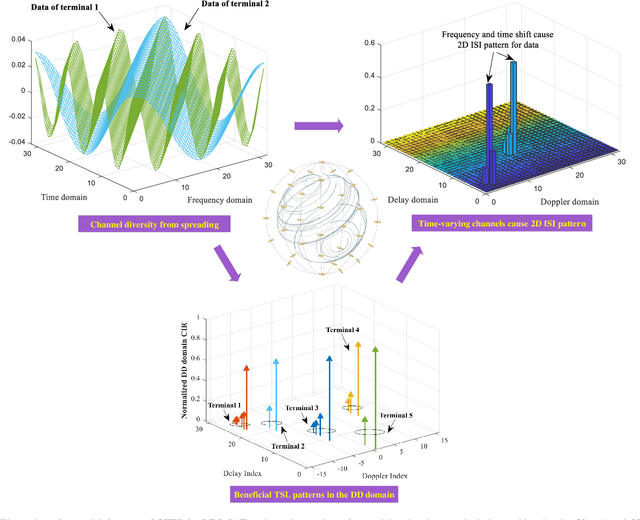
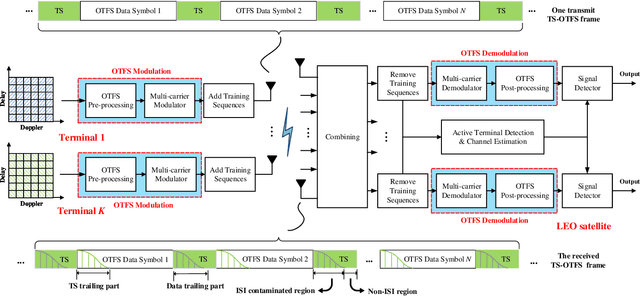
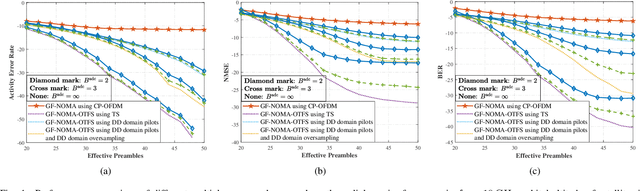
With the blooming of Internet-of-Things (IoT), we are witnessing an explosion in the number of IoT terminals, triggering an unprecedented demand for ubiquitous wireless access globally. In this context, the emerging low-Earth-orbit satellites (LEO-SATs) have been regarded as a promising enabler to complement terrestrial wireless networks in providing ubiquitous connectivity and bridging the ever-growing digital divide in the expected next-generation wireless communications. Nevertheless, the stringent requirements posed by LEO-SATs have imposed significant challenges to the current multiple access schemes and led to an emerging paradigm shift in system design. In this article, we first provide a comprehensive overview of the state-of-the-art multiple access schemes and investigate their limitations in the context of LEO-SATs. To this end, we propose the amalgamation of the grant-free non-orthogonal multiple access (GF-NOMA) paradigm and the orthogonal time frequency space (OTFS) waveform, for simplifying the connection procedure with reduced access latency and enhanced Doppler-robustness. Critical open challenging issues and future directions are finally presented for further technical development.

Reinforcement Learning for Self-exploration in Narrow Spaces

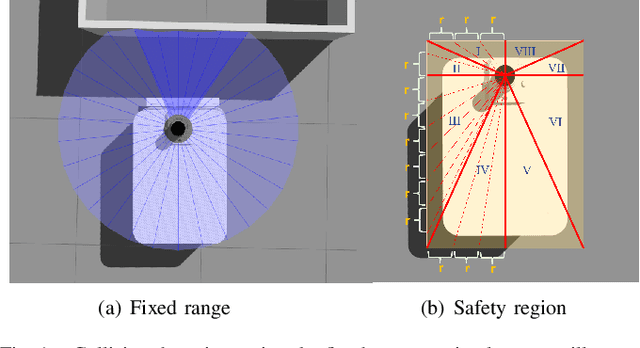
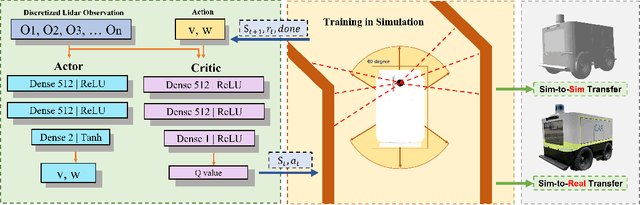
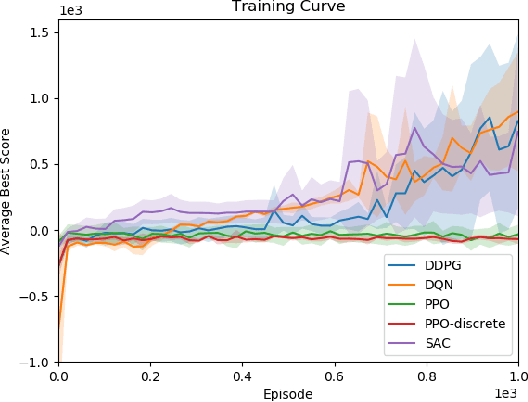
In narrow spaces, motion planning based on the traditional hierarchical autonomous system could cause collisions due to mapping, localization, and control noises. Additionally, it is disabled when mapless. To tackle these problems, we leverage deep reinforcement learning which is verified to be effective in self-decision-making, to self-explore in narrow spaces without a map while avoiding collisions. Specifically, based on our Ackermann-steering rectangular-shaped ZebraT robot and its Gazebo simulator, we propose the rectangular safety region to represent states and detect collisions for rectangular-shaped robots, and a carefully crafted reward function for reinforcement learning that does not require the destination information. Then we benchmark five reinforcement learning algorithms including DDPG, DQN, SAC, PPO, and PPO-discrete, in a simulated narrow track. After training, the well-performed DDPG and DQN models can be transferred to three brand new simulated tracks, and furthermore to three real-world tracks.