(Private) Kernelized Bandits with Distributed Biased Feedback

In this paper, we study kernelized bandits with distributed biased feedback. This problem is motivated by several real-world applications (such as dynamic pricing, cellular network configuration, and policy making), where users from a large population contribute to the reward of the action chosen by a central entity, but it is difficult to collect feedback from all users. Instead, only biased feedback (due to user heterogeneity) from a subset of users may be available. In addition to such partial biased feedback, we are also faced with two practical challenges due to communication cost and computation complexity. To tackle these challenges, we carefully design a new \emph{distributed phase-then-batch-based elimination (\texttt{DPBE})} algorithm, which samples users in phases for collecting feedback to reduce the bias and employs \emph{maximum variance reduction} to select actions in batches within each phase. By properly choosing the phase length, the batch size, and the confidence width used for eliminating suboptimal actions, we show that \texttt{DPBE} achieves a sublinear regret of $\tilde{O}(T^{1-\alpha/2}+\sqrt{\gamma_T T})$, where $\alpha\in (0,1)$ is the user-sampling parameter one can tune. Moreover, \texttt{DPBE} can significantly reduce both communication cost and computation complexity in distributed kernelized bandits, compared to some variants of the state-of-the-art algorithms (originally developed for standard kernelized bandits). Furthermore, by incorporating various \emph{differential privacy} models (including the central, local, and shuffle models), we generalize \texttt{DPBE} to provide privacy guarantees for users participating in the distributed learning process. Finally, we conduct extensive simulations to validate our theoretical results and evaluate the empirical performance.

Differentially Private Linear Bandits with Partial Distributed Feedback

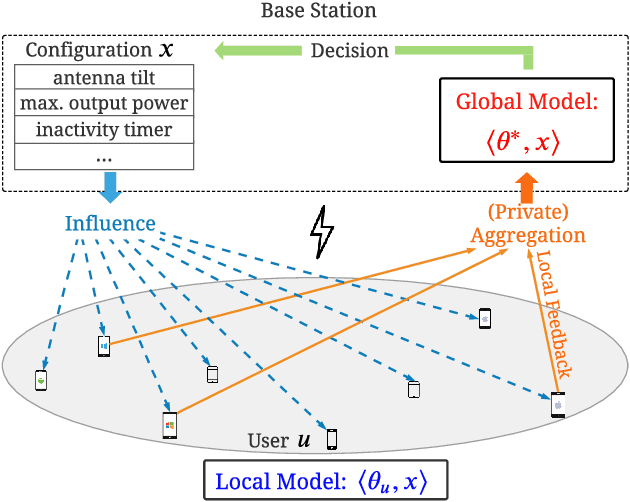
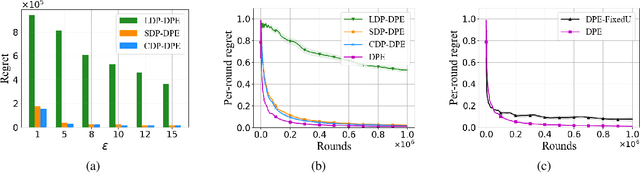
In this paper, we study the problem of global reward maximization with only partial distributed feedback. This problem is motivated by several real-world applications (e.g., cellular network configuration, dynamic pricing, and policy selection) where an action taken by a central entity influences a large population that contributes to the global reward. However, collecting such reward feedback from the entire population not only incurs a prohibitively high cost but often leads to privacy concerns. To tackle this problem, we consider differentially private distributed linear bandits, where only a subset of users from the population are selected (called clients) to participate in the learning process and the central server learns the global model from such partial feedback by iteratively aggregating these clients' local feedback in a differentially private fashion. We then propose a unified algorithmic learning framework, called differentially private distributed phased elimination (DP-DPE), which can be naturally integrated with popular differential privacy (DP) models (including central DP, local DP, and shuffle DP). Furthermore, we prove that DP-DPE achieves both sublinear regret and sublinear communication cost. Interestingly, DP-DPE also achieves privacy protection "for free" in the sense that the additional cost due to privacy guarantees is a lower-order additive term. In addition, as a by-product of our techniques, the same results of "free" privacy can also be achieved for the standard differentially private linear bandits. Finally, we conduct simulations to corroborate our theoretical results and demonstrate the effectiveness of DP-DPE.

Federated Learning with Fair Worker Selection: A Multi-Round Submodular Maximization Approach

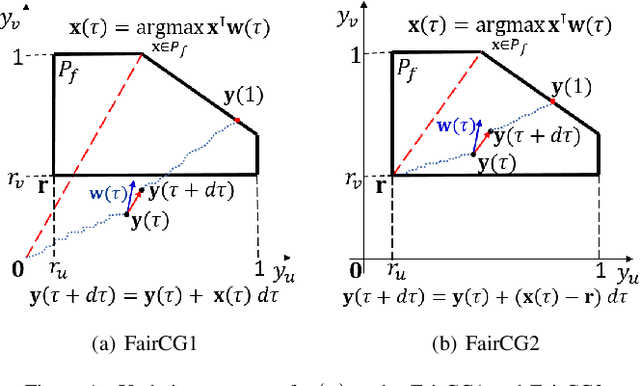
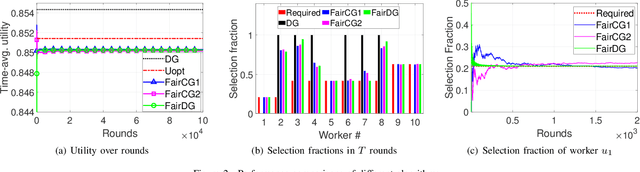
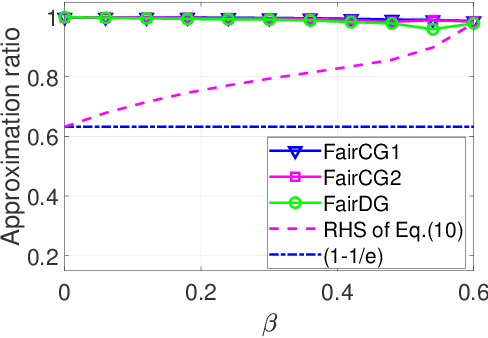
In this paper, we study the problem of fair worker selection in Federated Learning systems, where fairness serves as an incentive mechanism that encourages more workers to participate in the federation. Considering the achieved training accuracy of the global model as the utility of the selected workers, which is typically a monotone submodular function, we formulate the worker selection problem as a new multi-round monotone submodular maximization problem with cardinality and fairness constraints. The objective is to maximize the time-average utility over multiple rounds subject to an additional fairness requirement that each worker must be selected for a certain fraction of time. While the traditional submodular maximization with a cardinality constraint is already a well-known NP-Hard problem, the fairness constraint in the multi-round setting adds an extra layer of difficulty. To address this novel challenge, we propose three algorithms: Fair Continuous Greedy (FairCG1 and FairCG2) and Fair Discrete Greedy (FairDG), all of which satisfy the fairness requirement whenever feasible. Moreover, we prove nontrivial lower bounds on the achieved time-average utility under FairCG1 and FairCG2. In addition, by giving a higher priority to fairness, FairDG ensures a stronger short-term fairness guarantee, which holds in every round. Finally, we perform extensive simulations to verify the effectiveness of the proposed algorithms in terms of the time-average utility and fairness satisfaction.

Waiting but not Aging: Age-of-Information and Utility Optimization Under the Pull Model

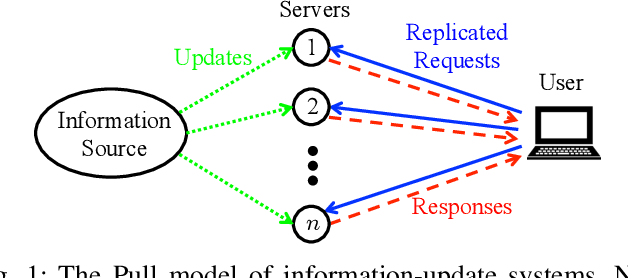
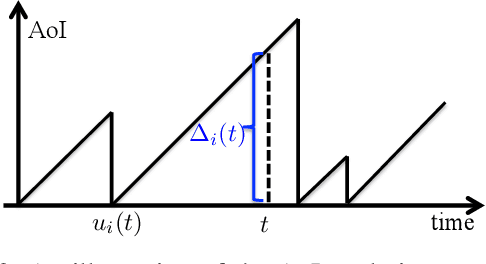
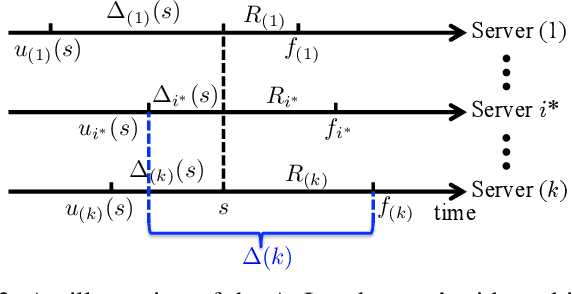
The Age-of-Information (AoI) has recently been proposed as an important metric for investigating the timeliness performance in information-update systems. In this paper, we introduce a new Pull model and study the AoI optimization problem under replication schemes. Interestingly, we find that under this new Pull model, replication schemes capture a novel tradeoff between different levels of information freshness and different response times across the servers, which can be exploited to minimize the expected AoI at the user's side. Specifically, assuming Poisson updating process for the servers and exponentially distributed response time, we derive a closed-form formula for computing the expected AoI and obtain the optimal number of responses to wait for to minimize the expected AoI. Then, we extend our analysis to the setting where the user aims to maximize the AoI-based utility, which represents the user's satisfaction level with respect to freshness of the received information. Furthermore, we consider a more realistic scenario where the user has no knowledge of the system. In this case, we reformulate the utility maximization problem as a stochastic Multi-Armed Bandit problem with side observations and leverage the unique structure of the problem to design learning algorithms with improved performance guarantees. Finally, we conduct extensive simulations to elucidate our theoretical results and compare the performance of different algorithms. Our findings reveal that under the Pull model, waiting for more than one response can significantly reduce the AoI and improve the AoI-based utility in most scenarios.

Combinatorial Sleeping Bandits with Fairness Constraints

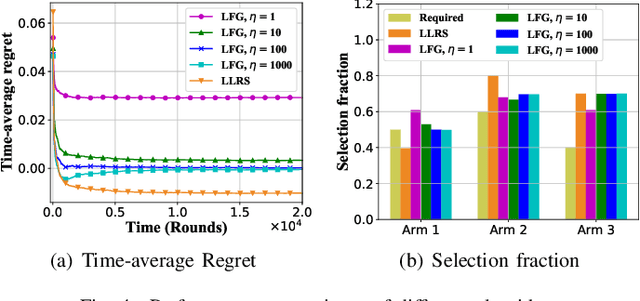
The multi-armed bandit (MAB) model has been widely adopted for studying many practical optimization problems (network resource allocation, ad placement, crowdsourcing, etc.) with unknown parameters. The goal of the player here is to maximize the cumulative reward in the face of uncertainty. However, the basic MAB model neglects several important factors of the system in many real-world applications, where multiple arms can be simultaneously played and an arm could sometimes be "sleeping". Besides, ensuring fairness is also a key design concern in practice. To that end, we propose a new Combinatorial Sleeping MAB model with Fairness constraints, called CSMAB-F, aiming to address the aforementioned crucial modeling issues. The objective is now to maximize the reward while satisfying the fairness requirement of a minimum selection fraction for each individual arm. To tackle this new problem, we extend an online learning algorithm, UCB, to deal with a critical tradeoff between exploitation and exploration and employ the virtual queue technique to properly handle the fairness constraints. By carefully integrating these two techniques, we develop a new algorithm, called Learning with Fairness Guarantee (LFG), for the CSMAB-F problem. Further, we rigorously prove that not only LFG is feasibility-optimal, but it also has a time-average regret upper bounded by $\frac{N}{2\eta}+\frac{\beta_1\sqrt{mNT\log{T}}+\beta_2 N}{T}$, where N is the total number of arms, m is the maximum number of arms that can be simultaneously played, T is the time horizon, $\beta_1$ and $\beta_2$ are constants, and $\eta$ is a design parameter that we can tune. Finally, we perform extensive simulations to corroborate the effectiveness of the proposed algorithm. Interestingly, the simulation results reveal an important tradeoff between the regret and the speed of convergence to a point satisfying the fairness constraints.