REWIND: Real-Time Egocentric Whole-Body Motion Diffusion with Exemplar-Based Identity Conditioning

We present REWIND (Real-Time Egocentric Whole-Body Motion Diffusion), a one-step diffusion model for real-time, high-fidelity human motion estimation from egocentric image inputs. While an existing method for egocentric whole-body (i.e., body and hands) motion estimation is non-real-time and acausal due to diffusion-based iterative motion refinement to capture correlations between body and hand poses, REWIND operates in a fully causal and real-time manner. To enable real-time inference, we introduce (1) cascaded body-hand denoising diffusion, which effectively models the correlation between egocentric body and hand motions in a fast, feed-forward manner, and (2) diffusion distillation, which enables high-quality motion estimation with a single denoising step. Our denoising diffusion model is based on a modified Transformer architecture, designed to causally model output motions while enhancing generalizability to unseen motion lengths. Additionally, REWIND optionally supports identity-conditioned motion estimation when identity prior is available. To this end, we propose a novel identity conditioning method based on a small set of pose exemplars of the target identity, which further enhances motion estimation quality. Through extensive experiments, we demonstrate that REWIND significantly outperforms the existing baselines both with and without exemplar-based identity conditioning.

No-regret Exploration in Shuffle Private Reinforcement Learning

Differential privacy (DP) has recently been introduced into episodic reinforcement learning (RL) to formally address user privacy concerns in personalized services. Previous work mainly focuses on two trust models of DP: the central model, where a central agent is responsible for protecting users' sensitive data, and the (stronger) local model, where the protection occurs directly on the user side. However, they either require a trusted central agent or incur a significantly higher privacy cost, making it unsuitable for many scenarios. This work introduces a trust model stronger than the central model but with a lower privacy cost than the local model, leveraging the emerging \emph{shuffle} model of privacy. We present the first generic algorithm for episodic RL under the shuffle model, where a trusted shuffler randomly permutes a batch of users' data before sending it to the central agent. We then instantiate the algorithm using our proposed shuffle Privatizer, relying on a shuffle private binary summation mechanism. Our analysis shows that the algorithm achieves a near-optimal regret bound comparable to that of the centralized model and significantly outperforms the local model in terms of privacy cost.

Universal Facial Encoding of Codec Avatars from VR Headsets

Faithful real-time facial animation is essential for avatar-mediated telepresence in Virtual Reality (VR). To emulate authentic communication, avatar animation needs to be efficient and accurate: able to capture both extreme and subtle expressions within a few milliseconds to sustain the rhythm of natural conversations. The oblique and incomplete views of the face, variability in the donning of headsets, and illumination variation due to the environment are some of the unique challenges in generalization to unseen faces. In this paper, we present a method that can animate a photorealistic avatar in realtime from head-mounted cameras (HMCs) on a consumer VR headset. We present a self-supervised learning approach, based on a cross-view reconstruction objective, that enables generalization to unseen users. We present a lightweight expression calibration mechanism that increases accuracy with minimal additional cost to run-time efficiency. We present an improved parameterization for precise ground-truth generation that provides robustness to environmental variation. The resulting system produces accurate facial animation for unseen users wearing VR headsets in realtime. We compare our approach to prior face-encoding methods demonstrating significant improvements in both quantitative metrics and qualitative results.

Fast Registration of Photorealistic Avatars for VR Facial Animation

Virtual Reality (VR) bares promise of social interactions that can feel more immersive than other media. Key to this is the ability to accurately animate a photorealistic avatar of one's likeness while wearing a VR headset. Although high quality registration of person-specific avatars to headset-mounted camera (HMC) images is possible in an offline setting, the performance of generic realtime models are significantly degraded. Online registration is also challenging due to oblique camera views and differences in modality. In this work, we first show that the domain gap between the avatar and headset-camera images is one of the primary sources of difficulty, where a transformer-based architecture achieves high accuracy on domain-consistent data, but degrades when the domain-gap is re-introduced. Building on this finding, we develop a system design that decouples the problem into two parts: 1) an iterative refinement module that takes in-domain inputs, and 2) a generic avatar-guided image-to-image style transfer module that is conditioned on current estimation of expression and head pose. These two modules reinforce each other, as image style transfer becomes easier when close-to-ground-truth examples are shown, and better domain-gap removal helps registration. Our system produces high-quality results efficiently, obviating the need for costly offline registration to generate personalized labels. We validate the accuracy and efficiency of our approach through extensive experiments on a commodity headset, demonstrating significant improvements over direct regression methods as well as offline registration.

From Audio to Photoreal Embodiment: Synthesizing Humans in Conversations

We present a framework for generating full-bodied photorealistic avatars that gesture according to the conversational dynamics of a dyadic interaction. Given speech audio, we output multiple possibilities of gestural motion for an individual, including face, body, and hands. The key behind our method is in combining the benefits of sample diversity from vector quantization with the high-frequency details obtained through diffusion to generate more dynamic, expressive motion. We visualize the generated motion using highly photorealistic avatars that can express crucial nuances in gestures (e.g. sneers and smirks). To facilitate this line of research, we introduce a first-of-its-kind multi-view conversational dataset that allows for photorealistic reconstruction. Experiments show our model generates appropriate and diverse gestures, outperforming both diffusion- and VQ-only methods. Furthermore, our perceptual evaluation highlights the importance of photorealism (vs. meshes) in accurately assessing subtle motion details in conversational gestures. Code and dataset available online.

Path Independent Equilibrium Models Can Better Exploit Test-Time Computation

Designing networks capable of attaining better performance with an increased inference budget is important to facilitate generalization to harder problem instances. Recent efforts have shown promising results in this direction by making use of depth-wise recurrent networks. We show that a broad class of architectures named equilibrium models display strong upwards generalization, and find that stronger performance on harder examples (which require more iterations of inference to get correct) strongly correlates with the path independence of the system -- its tendency to converge to the same steady-state behaviour regardless of initialization, given enough computation. Experimental interventions made to promote path independence result in improved generalization on harder problem instances, while those that penalize it degrade this ability. Path independence analyses are also useful on a per-example basis: for equilibrium models that have good in-distribution performance, path independence on out-of-distribution samples strongly correlates with accuracy. Our results help explain why equilibrium models are capable of strong upwards generalization and motivates future work that harnesses path independence as a general modelling principle to facilitate scalable test-time usage.

Stability of Weighted Majority Voting under Estimated Weights

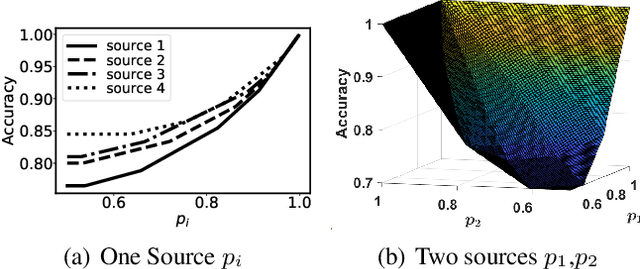
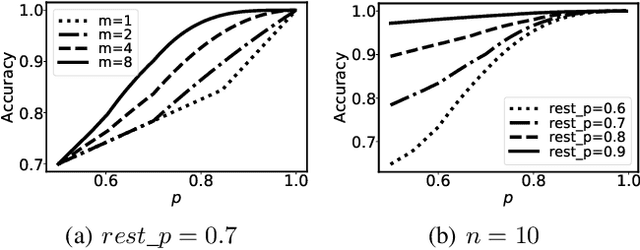
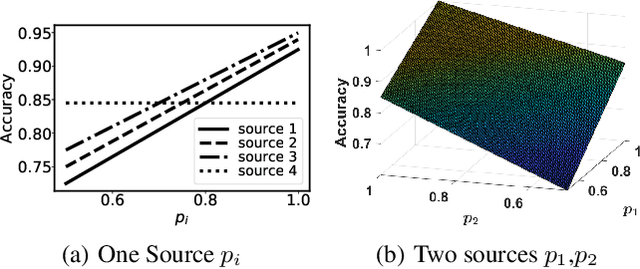
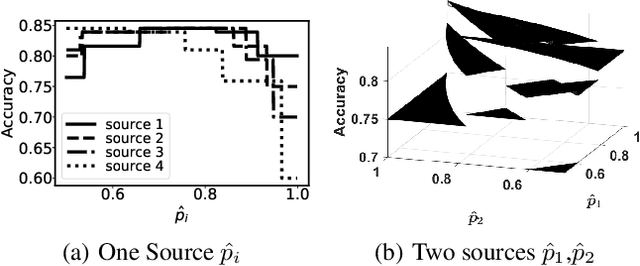
Weighted Majority Voting (WMV) is a well-known optimal decision rule for collective decision making, given the probability of sources to provide accurate information (trustworthiness). However, in reality, the trustworthiness is not a known quantity to the decision maker - they have to rely on an estimate called trust. A (machine learning) algorithm that computes trust is called unbiased when it has the property that it does not systematically overestimate or underestimate the trustworthiness. To formally analyse the uncertainty to the decision process, we introduce and analyse two important properties of such unbiased trust values: stability of correctness and stability of optimality. Stability of correctness means that the decision accuracy that the decision maker believes they achieved is equal to the actual accuracy. We prove stability of correctness holds. Stability of optimality means that the decisions made based on trust, are equally good as they would have been if they were based on trustworthiness. Stability of optimality does not hold. We analyse the difference between the two, and bounds thereon. We also present an overview of how sensitive decision correctness is to changes in trust and trustworthiness.

Deep Equilibrium Optical Flow Estimation

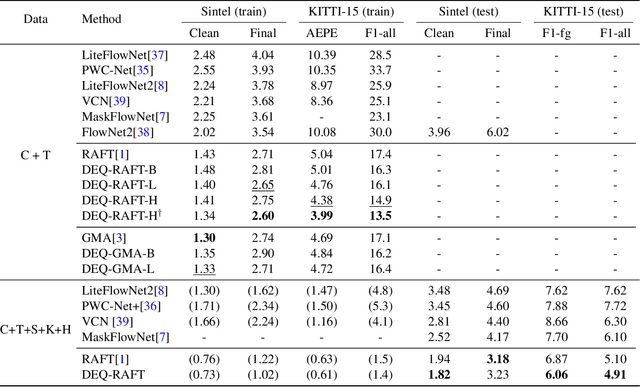
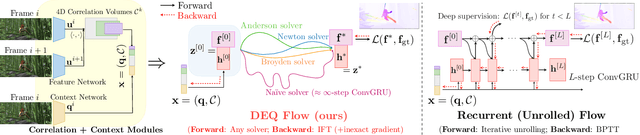
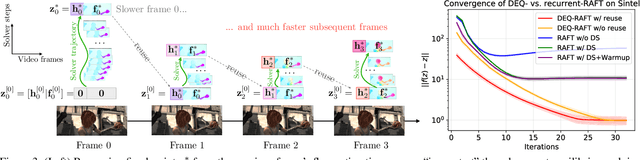
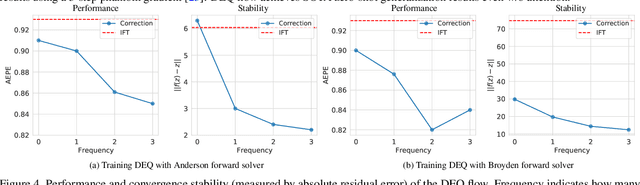
Many recent state-of-the-art (SOTA) optical flow models use finite-step recurrent update operations to emulate traditional algorithms by encouraging iterative refinements toward a stable flow estimation. However, these RNNs impose large computation and memory overheads, and are not directly trained to model such stable estimation. They can converge poorly and thereby suffer from performance degradation. To combat these drawbacks, we propose deep equilibrium (DEQ) flow estimators, an approach that directly solves for the flow as the infinite-level fixed point of an implicit layer (using any black-box solver), and differentiates through this fixed point analytically (thus requiring $O(1)$ training memory). This implicit-depth approach is not predicated on any specific model, and thus can be applied to a wide range of SOTA flow estimation model designs. The use of these DEQ flow estimators allows us to compute the flow faster using, e.g., fixed-point reuse and inexact gradients, consumes $4\sim6\times$ times less training memory than the recurrent counterpart, and achieves better results with the same computation budget. In addition, we propose a novel, sparse fixed-point correction scheme to stabilize our DEQ flow estimators, which addresses a longstanding challenge for DEQ models in general. We test our approach in various realistic settings and show that it improves SOTA methods on Sintel and KITTI datasets with substantially better computational and memory efficiency.

Joint inference and input optimization in equilibrium networks

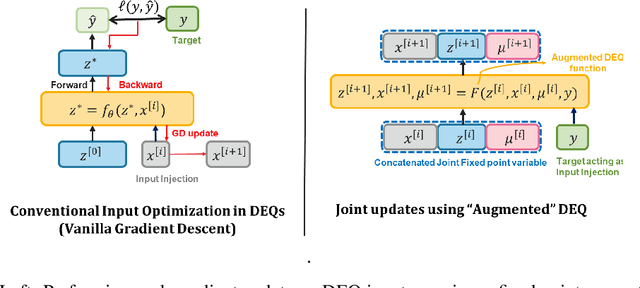
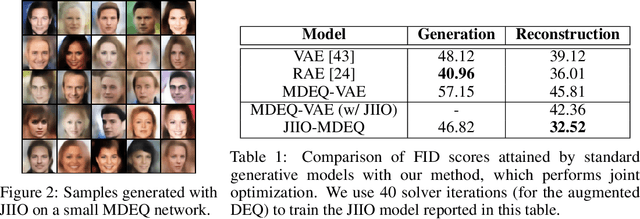
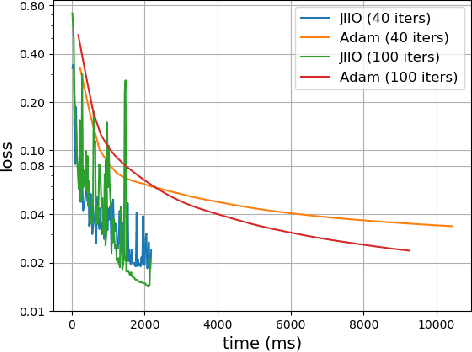
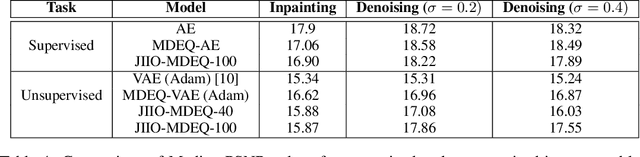
Many tasks in deep learning involve optimizing over the \emph{inputs} to a network to minimize or maximize some objective; examples include optimization over latent spaces in a generative model to match a target image, or adversarially perturbing an input to worsen classifier performance. Performing such optimization, however, is traditionally quite costly, as it involves a complete forward and backward pass through the network for each gradient step. In a separate line of work, a recent thread of research has developed the deep equilibrium (DEQ) model, a class of models that foregoes traditional network depth and instead computes the output of a network by finding the fixed point of a single nonlinear layer. In this paper, we show that there is a natural synergy between these two settings. Although, naively using DEQs for these optimization problems is expensive (owing to the time needed to compute a fixed point for each gradient step), we can leverage the fact that gradient-based optimization can \emph{itself} be cast as a fixed point iteration to substantially improve the overall speed. That is, we \emph{simultaneously} both solve for the DEQ fixed point \emph{and} optimize over network inputs, all within a single ``augmented'' DEQ model that jointly encodes both the original network and the optimization process. Indeed, the procedure is fast enough that it allows us to efficiently \emph{train} DEQ models for tasks traditionally relying on an ``inner'' optimization loop. We demonstrate this strategy on various tasks such as training generative models while optimizing over latent codes, training models for inverse problems like denoising and inpainting, adversarial training and gradient based meta-learning.

On Training Implicit Models

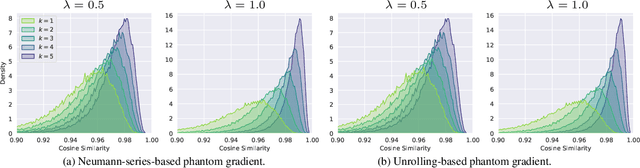
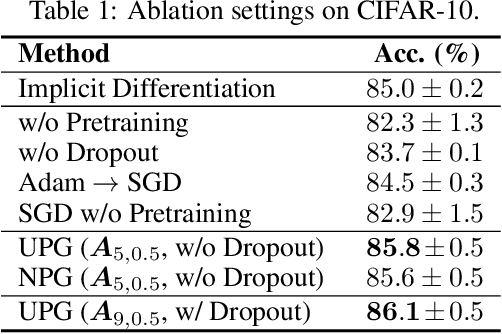
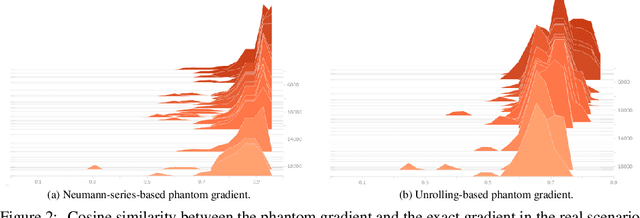
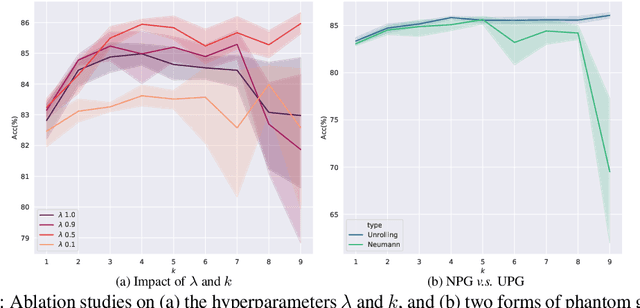
This paper focuses on training implicit models of infinite layers. Specifically, previous works employ implicit differentiation and solve the exact gradient for the backward propagation. However, is it necessary to compute such an exact but expensive gradient for training? In this work, we propose a novel gradient estimate for implicit models, named phantom gradient, that 1) forgoes the costly computation of the exact gradient; and 2) provides an update direction empirically preferable to the implicit model training. We theoretically analyze the condition under which an ascent direction of the loss landscape could be found, and provide two specific instantiations of the phantom gradient based on the damped unrolling and Neumann series. Experiments on large-scale tasks demonstrate that these lightweight phantom gradients significantly accelerate the backward passes in training implicit models by roughly 1.7 times, and even boost the performance over approaches based on the exact gradient on ImageNet.