GeoMotionGPT: Geometry-Aligned Motion Understanding with Large Language Models

Discrete motion tokenization has recently enabled Large Language Models (LLMs) to serve as versatile backbones for motion understanding and motion-language reasoning. However, existing pipelines typically decouple motion quantization from semantic embedding learning, linking them solely via token IDs. This approach fails to effectively align the intrinsic geometry of the motion space with the embedding space, thereby hindering the LLM's capacity for nuanced motion reasoning. We argue that alignment is most effective when both modalities share a unified geometric basis. Therefore, instead of forcing the LLM to reconstruct the complex geometry among motion tokens from scratch, we present a novel framework that explicitly enforces orthogonality on both the motion codebook and the LLM embedding space, ensuring that their relational structures naturally mirror each other. Specifically, we employ a decoder-only quantizer with Gumbel-Softmax for differentiable training and balanced codebook usage. To bridge the modalities, we use a sparse projection that maps motion codes into the LLM embedding space while preserving orthogonality. Finally, a two-stage orthonormal regularization schedule enforces soft constraints during tokenizer training and LLM fine-tuning to maintain geometric alignment without hindering semantic adaptation. Extensive experiments on HumanML3D demonstrate that our framework achieves a 20% performance improvement over current state-of-the-art methods, validating that a unified geometric basis effectively empowers the LLM for nuanced motion reasoning.

Dynamic Bayesian Optimization Framework for Instruction Tuning in Partial Differential Equation Discovery

Large Language Models (LLMs) show promise for equation discovery, yet their outputs are highly sensitive to prompt phrasing, a phenomenon we term instruction brittleness. Static prompts cannot adapt to the evolving state of a multi-step generation process, causing models to plateau at suboptimal solutions. To address this, we propose NeuroSymBO, which reframes prompt engineering as a sequential decision problem. Our method maintains a discrete library of reasoning strategies and uses Bayesian Optimization to select the optimal instruction at each step based on numerical feedback. Experiments on PDE discovery benchmarks show that adaptive instruction selection significantly outperforms fixed prompts, achieving higher recovery rates with more parsimonious solutions.

HyperEdit: Unlocking Instruction-based Text Editing in LLMs via Hypernetworks

Instruction-based text editing is increasingly critical for real-world applications such as code editors (e.g., Cursor), but Large Language Models (LLMs) continue to struggle with this task. Unlike free-form generation, editing requires faithfully implementing user instructions while preserving unchanged content, as even minor unintended modifications can break functionality. Existing approaches treat editing as generic text generation, leading to two key failures: they struggle to faithfully align edits with diverse user intents, and they often over-edit unchanged regions. We propose HyperEdit to address both issues. First, we introduce hypernetwork-based dynamic adaptation that generates request-specific parameters, enabling the model to tailor its editing strategy to each instruction. Second, we develop difference-aware regularization that focuses supervision on modified spans, preventing over-editing while ensuring precise, minimal changes. HyperEdit achieves a 9%--30% relative improvement in BLEU on modified regions over state-of-the-art baselines, despite utilizing only 3B parameters.

Cost-Aware Contrastive Routing for LLMs

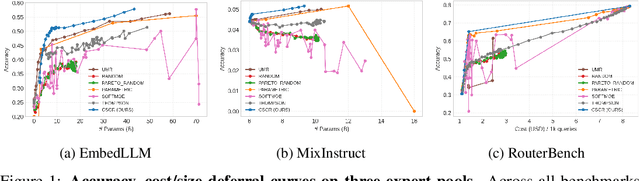
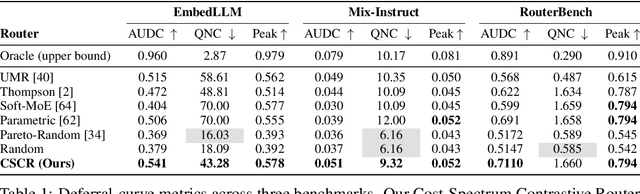
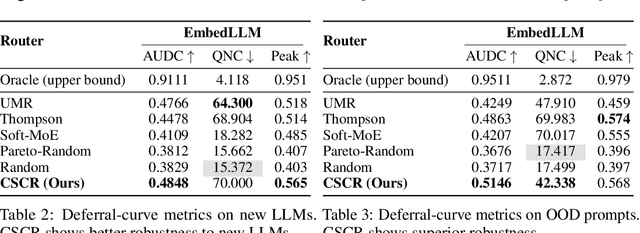
We study cost-aware routing for large language models across diverse and dynamic pools of models. Existing approaches often overlook prompt-specific context, rely on expensive model profiling, assume a fixed set of experts, or use inefficient trial-and-error strategies. We introduce Cost-Spectrum Contrastive Routing (CSCR), a lightweight framework that maps both prompts and models into a shared embedding space to enable fast, cost-sensitive selection. CSCR uses compact, fast-to-compute logit footprints for open-source models and perplexity fingerprints for black-box APIs. A contrastive encoder is trained to favor the cheapest accurate expert within adaptive cost bands. At inference time, routing reduces to a single k-NN lookup via a FAISS index, requiring no retraining when the expert pool changes and enabling microsecond latency. Across multiple benchmarks, CSCR consistently outperforms baselines, improving the accuracy-cost tradeoff by up to 25%, while generalizing robustly to unseen LLMs and out-of-distribution prompts.

ALTER: All-in-One Layer Pruning and Temporal Expert Routing for Efficient Diffusion Generation

Diffusion models have demonstrated exceptional capabilities in generating high-fidelity images. However, their iterative denoising process results in significant computational overhead during inference, limiting their practical deployment in resource-constrained environments. Existing acceleration methods often adopt uniform strategies that fail to capture the temporal variations during diffusion generation, while the commonly adopted sequential pruning-then-fine-tuning strategy suffers from sub-optimality due to the misalignment between pruning decisions made on pretrained weights and the model's final parameters. To address these limitations, we introduce ALTER: All-in-One Layer Pruning and Temporal Expert Routing, a unified framework that transforms diffusion models into a mixture of efficient temporal experts. ALTER achieves a single-stage optimization that unifies layer pruning, expert routing, and model fine-tuning by employing a trainable hypernetwork, which dynamically generates layer pruning decisions and manages timestep routing to specialized, pruned expert sub-networks throughout the ongoing fine-tuning of the UNet. This unified co-optimization strategy enables significant efficiency gains while preserving high generative quality. Specifically, ALTER achieves same-level visual fidelity to the original 50-step Stable Diffusion v2.1 model while utilizing only 25.9% of its total MACs with just 20 inference steps and delivering a 3.64x speedup through 35% sparsity.

Any Large Language Model Can Be a Reliable Judge: Debiasing with a Reasoning-based Bias Detector

LLM-as-a-Judge has emerged as a promising tool for automatically evaluating generated outputs, but its reliability is often undermined by potential biases in judgment. Existing efforts to mitigate these biases face key limitations: in-context learning-based methods fail to address rooted biases due to the evaluator's limited capacity for self-reflection, whereas fine-tuning is not applicable to all evaluator types, especially closed-source models. To address this challenge, we introduce the Reasoning-based Bias Detector (RBD), which is a plug-in module that identifies biased evaluations and generates structured reasoning to guide evaluator self-correction. Rather than modifying the evaluator itself, RBD operates externally and engages in an iterative process of bias detection and feedback-driven revision. To support its development, we design a complete pipeline consisting of biased dataset construction, supervision collection, distilled reasoning-based fine-tuning of RBD, and integration with LLM evaluators. We fine-tune four sizes of RBD models, ranging from 1.5B to 14B, and observe consistent performance improvements across all scales. Experimental results on 4 bias types--verbosity, position, bandwagon, and sentiment--evaluated using 8 LLM evaluators demonstrate RBD's strong effectiveness. For example, the RBD-8B model improves evaluation accuracy by an average of 18.5% and consistency by 10.9%, and surpasses prompting-based baselines and fine-tuned judges by 12.8% and 17.2%, respectively. These results highlight RBD's effectiveness and scalability. Additional experiments further demonstrate its strong generalization across biases and domains, as well as its efficiency.

Dynamic Noise Preference Optimization for LLM Self-Improvement via Synthetic Data

Although LLMs have achieved significant success, their reliance on large volumes of human-annotated data has limited their potential for further scaling. In this situation, utilizing self-generated synthetic data has become crucial for fine-tuning LLMs without extensive human annotation. However, current methods often fail to ensure consistent improvements across iterations, with performance stagnating after only minimal updates. To overcome these challenges, we introduce Dynamic Noise Preference Optimization (DNPO). DNPO employs a dynamic sample labeling mechanism to construct preference pairs for training and introduces controlled, trainable noise into the preference optimization process. Our approach effectively prevents stagnation and enables continuous improvement. In experiments with Zephyr-7B, DNPO consistently outperforms existing methods, showing an average performance boost of 2.6% across multiple benchmarks. Additionally, DNPO shows a significant improvement in model-generated data quality, with a 29.4% win-loss rate gap compared to the baseline in GPT-4 evaluations. This highlights its effectiveness in enhancing model performance through iterative refinement.

ToMoE: Converting Dense Large Language Models to Mixture-of-Experts through Dynamic Structural Pruning

Large Language Models (LLMs) have demonstrated remarkable abilities in tackling a wide range of complex tasks. However, their huge computational and memory costs raise significant challenges in deploying these models on resource-constrained devices or efficiently serving them. Prior approaches have attempted to alleviate these problems by permanently removing less important model structures, yet these methods often result in substantial performance degradation due to the permanent deletion of model parameters. In this work, we tried to mitigate this issue by reducing the number of active parameters without permanently removing them. Specifically, we introduce a differentiable dynamic pruning method that pushes dense models to maintain a fixed number of active parameters by converting their MLP layers into a Mixture of Experts (MoE) architecture. Our method, even without fine-tuning, consistently outperforms previous structural pruning techniques across diverse model families, including Phi-2, LLaMA-2, LLaMA-3, and Qwen-2.5.

FlexiGPT: Pruning and Extending Large Language Models with Low-Rank Weight Sharing

The rapid proliferation of large language models (LLMs) in natural language processing (NLP) has created a critical need for techniques that enable efficient deployment on memory-constrained devices without compromising performance. We present a method to prune LLMs that selectively prunes model blocks based on an importance score and replaces them with a low-parameter replacement strategy. Specifically, we propose a principled metric to replace each pruned block using a weight-sharing mechanism that leverages unpruned counterparts from the model and block-specific low-rank adapters. Furthermore, we facilitate the learning of these replacement blocks with output feature normalization and an adapter initialization scheme built on low-rank SVD reconstructions. Empirical evaluations demonstrate substantial performance gains over existing methods, achieving state-of-the-art performance on 5/6 benchmarks for a compression rate of 30% and 6/6 benchmarks for a compression rate of 40%. We also demonstrate that our approach can extend smaller models, boosting performance on 6/6 benchmarks using only ~0.3% tokens of extended training with minimal additional parameter costs.

All-in-One Tuning and Structural Pruning for Domain-Specific LLMs

Existing pruning techniques for large language models (LLMs) targeting domain-specific applications typically follow a two-stage process: pruning the pretrained general-purpose LLMs and then fine-tuning the pruned LLMs on specific domains. However, the pruning decisions, derived from the pretrained weights, remain unchanged during fine-tuning, even if the weights have been updated. Therefore, such a combination of the pruning decisions and the finetuned weights may be suboptimal, leading to non-negligible performance degradation. To address these limitations, we propose ATP: All-in-One Tuning and Structural Pruning, a unified one-stage structural pruning and fine-tuning approach that dynamically identifies the current optimal substructure throughout the fine-tuning phase via a trainable pruning decision generator. Moreover, given the limited available data for domain-specific applications, Low-Rank Adaptation (LoRA) becomes a common technique to fine-tune the LLMs. In ATP, we introduce LoRA-aware forward and sparsity regularization to ensure that the substructures corresponding to the learned pruning decisions can be directly removed after the ATP process. ATP outperforms the state-of-the-art two-stage pruning methods on tasks in the legal and healthcare domains. More specifically, ATP recovers up to 88% and 91% performance of the dense model when pruning 40% parameters of LLaMA2-7B and LLaMA3-8B models, respectively.