AutoML for Large Capacity Modeling of Meta's Ranking Systems

Web-scale ranking systems at Meta serving billions of users is complex. Improving ranking models is essential but engineering heavy. Automated Machine Learning (AutoML) can release engineers from labor intensive work of tuning ranking models; however, it is unknown if AutoML is efficient enough to meet tight production timeline in real-world and, at the same time, bring additional improvements to the strong baselines. Moreover, to achieve higher ranking performance, there is an ever-increasing demand to scale up ranking models to even larger capacity, which imposes more challenges on the efficiency. The large scale of models and tight production schedule requires AutoML to outperform human baselines by only using a small number of model evaluation trials (around 100). We presents a sampling-based AutoML method, focusing on neural architecture search and hyperparameter optimization, addressing these challenges in Meta-scale production when building large capacity models. Our approach efficiently handles large-scale data demands. It leverages a lightweight predictor-based searcher and reinforcement learning to explore vast search spaces, significantly reducing the number of model evaluations. Through experiments in large capacity modeling for CTR and CVR applications, we show that our method achieves outstanding Return on Investment (ROI) versus human tuned baselines, with up to 0.09% Normalized Entropy (NE) loss reduction or $25\%$ Query per Second (QPS) increase by only sampling one hundred models on average from a curated search space. The proposed AutoML method has already made real-world impact where a discovered Instagram CTR model with up to -0.36% NE gain (over existing production baseline) was selected for large-scale online A/B test and show statistically significant gain. These production results proved AutoML efficacy and accelerated its adoption in ranking systems at Meta.

Efficient Nonmyopic Bayesian Optimization via One-Shot Multi-Step Trees

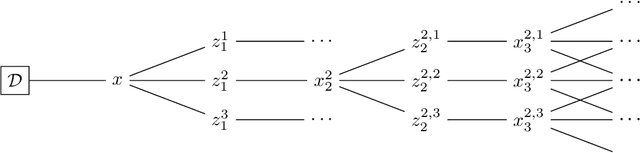
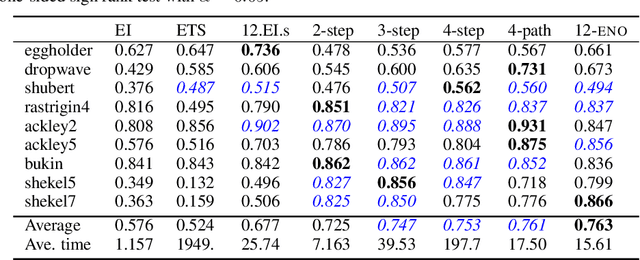
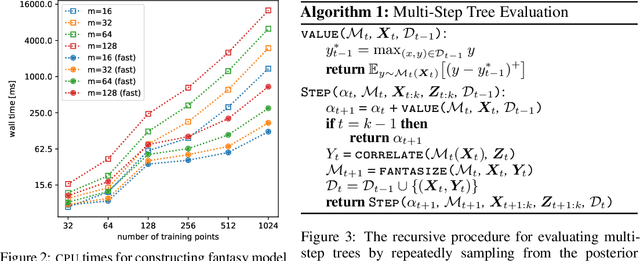
Bayesian optimization is a sequential decision making framework for optimizing expensive-to-evaluate black-box functions. Computing a full lookahead policy amounts to solving a highly intractable stochastic dynamic program. Myopic approaches, such as expected improvement, are often adopted in practice, but they ignore the long-term impact of the immediate decision. Existing nonmyopic approaches are mostly heuristic and/or computationally expensive. In this paper, we provide the first efficient implementation of general multi-step lookahead Bayesian optimization, formulated as a sequence of nested optimization problems within a multi-step scenario tree. Instead of solving these problems in a nested way, we equivalently optimize all decision variables in the full tree jointly, in a ``one-shot'' fashion. Combining this with an efficient method for implementing multi-step Gaussian process ``fantasization,'' we demonstrate that multi-step expected improvement is computationally tractable and exhibits performance superior to existing methods on a wide range of benchmarks.

Nearly Optimal Risk Bounds for Kernel K-Means

In this paper, we study the statistical properties of the kernel $k$-means and obtain a nearly optimal excess risk bound, substantially improving the state-of-art bounds in the existing clustering risk analyses. We further analyze the statistical effect of computational approximations of the Nystr\"{o}m kernel $k$-means, and demonstrate that it achieves the same statistical accuracy as the exact kernel $k$-means considering only $\sqrt{nk}$ Nystr\"{o}m landmark points. To the best of our knowledge, such sharp excess risk bounds for kernel (or approximate kernel) $k$-means have never been seen before.

Efficient nonmyopic Bayesian optimization and quadrature

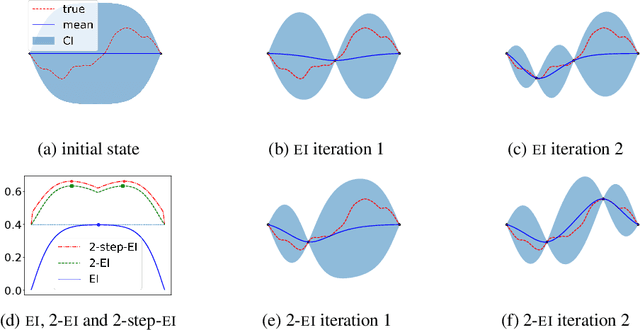
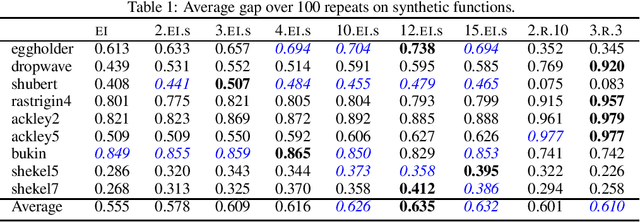
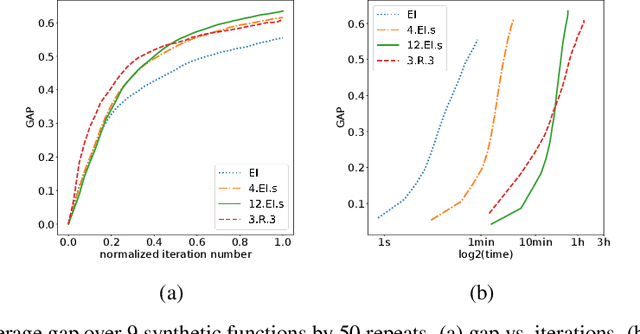
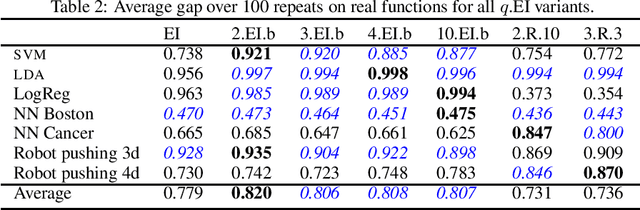
Finite-horizon sequential decision problems arise naturally in many machine learning contexts, including Bayesian optimization and Bayesian quadrature. Computing the optimal policy for such problems requires solving Bellman equations, which are generally intractable. Most existing work resorts to myopic approximations by limiting the decision horizon to only a single time-step, which can perform poorly at balancing exploration and exploitation. We propose a general framework for efficient, nonmyopic approximation of the optimal policy by drawing a connection between the optimal adaptive policy and its non-adaptive counterpart. Our proposal is to compute an optimal batch of points, then select a single point from within this batch to evaluate. We realize this idea for both Bayesian optimization and Bayesian quadrature and demonstrate that our proposed method significantly outperforms common myopic alternatives on a variety of tasks.

D-VAE: A Variational Autoencoder for Directed Acyclic Graphs

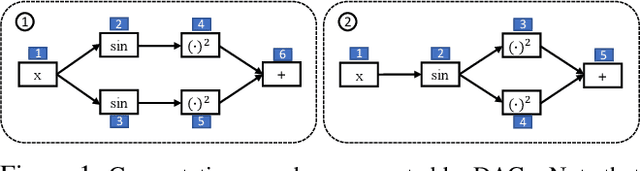
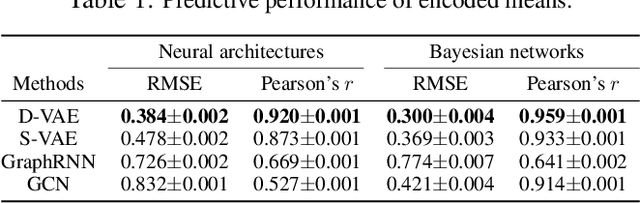
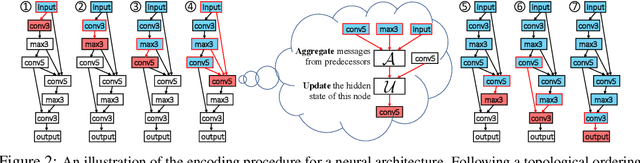
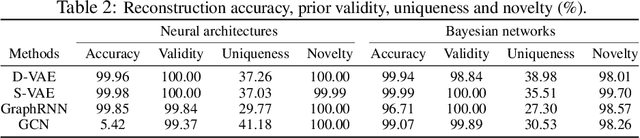
Graph structured data are abundant in the real world. Among different graph types, directed acyclic graphs (DAGs) are of particular interest to machine learning researchers, as many machine learning models are realized as computations on DAGs, including neural networks and Bayesian networks. In this paper, we study deep generative models for DAGs, and propose a novel DAG variational autoencoder (D-VAE). To encode DAGs into the latent space, we leverage graph neural networks. We propose an asynchronous message passing scheme that allows encoding the computations on DAGs, rather than using existing simultaneous message passing schemes to encode local graph structures. We demonstrate the effectiveness of our proposed D-VAE through two tasks: neural architecture search and Bayesian network structure learning. Experiments show that our model not only generates novel and valid DAGs, but also produces a smooth latent space that facilitates searching for DAGs with better performance through Bayesian optimization.

Efficient nonmyopic active search with applications in drug and materials discovery

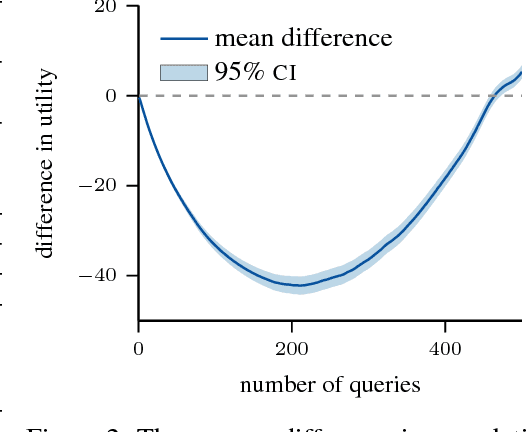
Active search is a learning paradigm for actively identifying as many members of a given class as possible. A critical target scenario is high-throughput screening for scientific discovery, such as drug or materials discovery. In this paper, we approach this problem in Bayesian decision framework. We first derive the Bayesian optimal policy under a natural utility, and establish a theoretical hardness of active search, proving that the optimal policy can not be approximated for any constant ratio. We also study the batch setting for the first time, where a batch of $b>1$ points can be queried at each iteration. We give an asymptotic lower bound, linear in batch size, on the adaptivity gap: how much we could lose if we query $b$ points at a time for $t$ iterations, instead of one point at a time for $bt$ iterations. We then introduce a novel approach to nonmyopic approximations of the optimal policy that admits efficient computation. Our proposed policy can automatically trade off exploration and exploitation, without relying on any tuning parameters. We also generalize our policy to batch setting, and propose two approaches to tackle the combinatorial search challenge. We evaluate our proposed policies on a large database of drug discovery and materials science. Results demonstrate the superior performance of our proposed policy in both sequential and batch setting; the nonmyopic behavior is also illustrated in various aspects.