Set Block Decoding is a Language Model Inference Accelerator

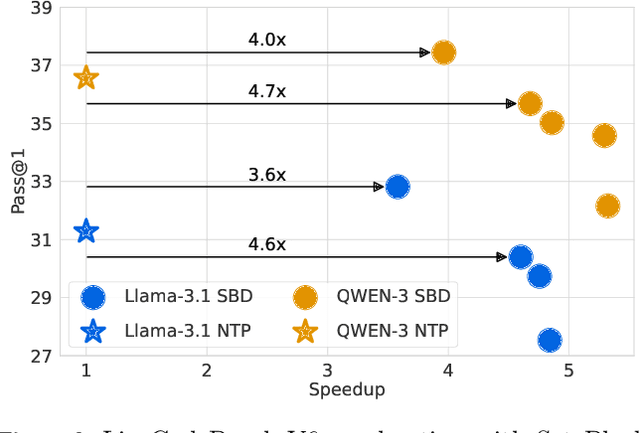
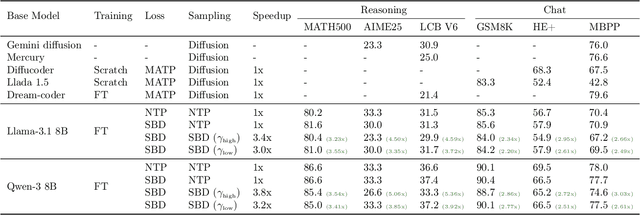
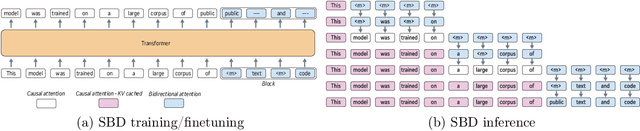
Autoregressive next token prediction language models offer powerful capabilities but face significant challenges in practical deployment due to the high computational and memory costs of inference, particularly during the decoding stage. We introduce Set Block Decoding (SBD), a simple and flexible paradigm that accelerates generation by integrating standard next token prediction (NTP) and masked token prediction (MATP) within a single architecture. SBD allows the model to sample multiple, not necessarily consecutive, future tokens in parallel, a key distinction from previous acceleration methods. This flexibility allows the use of advanced solvers from the discrete diffusion literature, offering significant speedups without sacrificing accuracy. SBD requires no architectural changes or extra training hyperparameters, maintains compatibility with exact KV-caching, and can be implemented by fine-tuning existing next token prediction models. By fine-tuning Llama-3.1 8B and Qwen-3 8B, we demonstrate that SBD enables a 3-5x reduction in the number of forward passes required for generation while achieving same performance as equivalent NTP training.

Edit Flows: Flow Matching with Edit Operations

Autoregressive generative models naturally generate variable-length sequences, while non-autoregressive models struggle, often imposing rigid, token-wise structures. We propose Edit Flows, a non-autoregressive model that overcomes these limitations by defining a discrete flow over sequences through edit operations-insertions, deletions, and substitutions. By modeling these operations within a Continuous-time Markov Chain over the sequence space, Edit Flows enable flexible, position-relative generation that aligns more closely with the structure of sequence data. Our training method leverages an expanded state space with auxiliary variables, making the learning process efficient and tractable. Empirical results show that Edit Flows outperforms both autoregressive and mask models on image captioning and significantly outperforms the mask construction in text and code generation.

Accelerated Sampling from Masked Diffusion Models via Entropy Bounded Unmasking

Recent masked diffusion models (MDMs) have shown competitive performance compared to autoregressive models (ARMs) for language modeling. While most literature has focused on performance enhancing sampling procedures, efficient sampling from MDMs has been scarcely explored. We make the observation that often a given sequence of partially masked tokens determines the values of multiple unknown tokens deterministically, meaning that a single prediction of a masked model holds additional information unused by standard sampling procedures. Based on this observation, we introduce EB-Sampler, a simple drop-in replacement for existing samplers, utilizing an Entropy Bounded unmasking procedure that dynamically unmasks multiple tokens in one function evaluation with predefined approximate error tolerance. We formulate the EB-Sampler as part of a broad family of adaptive samplers for which we provide an error analysis that motivates our algorithmic choices. EB-Sampler accelerates sampling from current state of the art MDMs by roughly 2-3x on standard coding and math reasoning benchmarks without loss in performance. We also validate the same procedure works well on smaller reasoning tasks including maze navigation and Sudoku, tasks ARMs often struggle with.

Learning Distributions over Permutations and Rankings with Factorized Representations

Learning distributions over permutations is a fundamental problem in machine learning, with applications in ranking, combinatorial optimization, structured prediction, and data association. Existing methods rely on mixtures of parametric families or neural networks with expensive variational inference procedures. In this work, we propose a novel approach that leverages alternative representations for permutations, including Lehmer codes, Fisher-Yates draws, and Insertion-Vectors. These representations form a bijection with the symmetric group, allowing for unconstrained learning using conventional deep learning techniques, and can represent any probability distribution over permutations. Our approach enables a trade-off between expressivity of the model family and computational requirements. In the least expressive and most computationally efficient case, our method subsumes previous families of well established probabilistic models over permutations, including Mallow's and the Repeated Insertion Model. Experiments indicate our method significantly outperforms current approaches on the jigsaw puzzle benchmark, a common task for permutation learning. However, we argue this benchmark is limited in its ability to assess learning probability distributions, as the target is a delta distribution (i.e., a single correct solution exists). We therefore propose two additional benchmarks: learning cyclic permutations and re-ranking movies based on user preference. We show that our method learns non-trivial distributions even in the least expressive mode, while traditional models fail to even generate valid permutations in this setting.

Adjoint Sampling: Highly Scalable Diffusion Samplers via Adjoint Matching

We introduce Adjoint Sampling, a highly scalable and efficient algorithm for learning diffusion processes that sample from unnormalized densities, or energy functions. It is the first on-policy approach that allows significantly more gradient updates than the number of energy evaluations and model samples, allowing us to scale to much larger problem settings than previously explored by similar methods. Our framework is theoretically grounded in stochastic optimal control and shares the same theoretical guarantees as Adjoint Matching, being able to train without the need for corrective measures that push samples towards the target distribution. We show how to incorporate key symmetries, as well as periodic boundary conditions, for modeling molecules in both cartesian and torsional coordinates. We demonstrate the effectiveness of our approach through extensive experiments on classical energy functions, and further scale up to neural network-based energy models where we perform amortized conformer generation across many molecular systems. To encourage further research in developing highly scalable sampling methods, we plan to open source these challenging benchmarks, where successful methods can directly impact progress in computational chemistry.

Flow Matching Guide and Code

Flow Matching (FM) is a recent framework for generative modeling that has achieved state-of-the-art performance across various domains, including image, video, audio, speech, and biological structures. This guide offers a comprehensive and self-contained review of FM, covering its mathematical foundations, design choices, and extensions. By also providing a PyTorch package featuring relevant examples (e.g., image and text generation), this work aims to serve as a resource for both novice and experienced researchers interested in understanding, applying and further developing FM.

Flow Matching with General Discrete Paths: A Kinetic-Optimal Perspective

The design space of discrete-space diffusion or flow generative models are significantly less well-understood than their continuous-space counterparts, with many works focusing only on a simple masked construction. In this work, we aim to take a holistic approach to the construction of discrete generative models based on continuous-time Markov chains, and for the first time, allow the use of arbitrary discrete probability paths, or colloquially, corruption processes. Through the lens of optimizing the symmetric kinetic energy, we propose velocity formulas that can be applied to any given probability path, completely decoupling the probability and velocity, and giving the user the freedom to specify any desirable probability path based on expert knowledge specific to the data domain. Furthermore, we find that a special construction of mixture probability paths optimizes the symmetric kinetic energy for the discrete case. We empirically validate the usefulness of this new design space across multiple modalities: text generation, inorganic material generation, and image generation. We find that we can outperform the mask construction even in text with kinetic-optimal mixture paths, while we can make use of domain-specific constructions of the probability path over the visual domain.

Generator Matching: Generative modeling with arbitrary Markov processes

We introduce generator matching, a modality-agnostic framework for generative modeling using arbitrary Markov processes. Generators characterize the infinitesimal evolution of a Markov process, which we leverage for generative modeling in a similar vein to flow matching: we construct conditional generators which generate single data points, then learn to approximate the marginal generator which generates the full data distribution. We show that generator matching unifies various generative modeling methods, including diffusion models, flow matching and discrete diffusion models. Furthermore, it provides the foundation to expand the design space to new and unexplored Markov processes such as jump processes. Finally, generator matching enables the construction of superpositions of Markov generative processes and enables the construction of multimodal models in a rigorous manner. We empirically validate our method on protein and image structure generation, showing that superposition with a jump process improves image generation.

Adjoint Matching: Fine-tuning Flow and Diffusion Generative Models with Memoryless Stochastic Optimal Control

Dynamical generative models that produce samples through an iterative process, such as Flow Matching and denoising diffusion models, have seen widespread use, but there has not been many theoretically-sound methods for improving these models with reward fine-tuning. In this work, we cast reward fine-tuning as stochastic optimal control (SOC). Critically, we prove that a very specific memoryless noise schedule must be enforced during fine-tuning, in order to account for the dependency between the noise variable and the generated samples. We also propose a new algorithm named Adjoint Matching which outperforms existing SOC algorithms, by casting SOC problems as a regression problem. We find that our approach significantly improves over existing methods for reward fine-tuning, achieving better consistency, realism, and generalization to unseen human preference reward models, while retaining sample diversity.

D-Flow: Differentiating through Flows for Controlled Generation

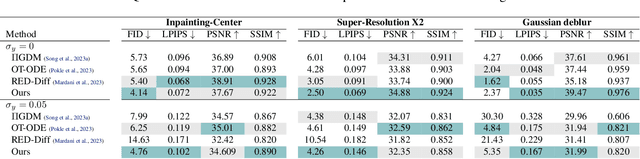
Taming the generation outcome of state of the art Diffusion and Flow-Matching (FM) models without having to re-train a task-specific model unlocks a powerful tool for solving inverse problems, conditional generation, and controlled generation in general. In this work we introduce D-Flow, a simple framework for controlling the generation process by differentiating through the flow, optimizing for the source (noise) point. We motivate this framework by our key observation stating that for Diffusion/FM models trained with Gaussian probability paths, differentiating through the generation process projects gradient on the data manifold, implicitly injecting the prior into the optimization process. We validate our framework on linear and non-linear controlled generation problems including: image and audio inverse problems and conditional molecule generation reaching state of the art performance across all.