Model Sparsification Can Simplify Machine Unlearning

Recent data regulations necessitate machine unlearning (MU): The removal of the effect of specific examples from the model. While exact unlearning is possible by conducting a model retraining with the remaining data from scratch, its computational cost has led to the development of approximate but efficient unlearning schemes. Beyond data-centric MU solutions, we advance MU through a novel model-based viewpoint: sparsification via weight pruning. Our results in both theory and practice indicate that model sparsity can boost the multi-criteria unlearning performance of an approximate unlearner, closing the approximation gap, while continuing to be efficient. With this insight, we develop two new sparsity-aware unlearning meta-schemes, termed `prune first, then unlearn' and `sparsity-aware unlearning'. Extensive experiments show that our findings and proposals consistently benefit MU in various scenarios, including class-wise data scrubbing, random data scrubbing, and backdoor data forgetting. One highlight is the 77% unlearning efficacy gain of fine-tuning (one of the simplest approximate unlearning methods) in the proposed sparsity-aware unlearning paradigm. Codes are available at https://github.com/OPTML-Group/Unlearn-Sparse.

What Is Missing in IRM Training and Evaluation? Challenges and Solutions

Invariant risk minimization (IRM) has received increasing attention as a way to acquire environment-agnostic data representations and predictions, and as a principled solution for preventing spurious correlations from being learned and for improving models' out-of-distribution generalization. Yet, recent works have found that the optimality of the originally-proposed IRM optimization (IRM) may be compromised in practice or could be impossible to achieve in some scenarios. Therefore, a series of advanced IRM algorithms have been developed that show practical improvement over IRM. In this work, we revisit these recent IRM advancements, and identify and resolve three practical limitations in IRM training and evaluation. First, we find that the effect of batch size during training has been chronically overlooked in previous studies, leaving room for further improvement. We propose small-batch training and highlight the improvements over a set of large-batch optimization techniques. Second, we find that improper selection of evaluation environments could give a false sense of invariance for IRM. To alleviate this effect, we leverage diversified test-time environments to precisely characterize the invariance of IRM when applied in practice. Third, we revisit (Ahuja et al. (2020))'s proposal to convert IRM into an ensemble game and identify a limitation when a single invariant predictor is desired instead of an ensemble of individual predictors. We propose a new IRM variant to address this limitation based on a novel viewpoint of ensemble IRM games as consensus-constrained bi-level optimization. Lastly, we conduct extensive experiments (covering 7 existing IRM variants and 7 datasets) to justify the practical significance of revisiting IRM training and evaluation in a principled manner.

Federated Minimax Optimization with Client Heterogeneity

Minimax optimization has seen a surge in interest with the advent of modern applications such as GANs, and it is inherently more challenging than simple minimization. The difficulty is exacerbated by the training data residing at multiple edge devices or \textit{clients}, especially when these clients can have heterogeneous datasets and local computation capabilities. We propose a general federated minimax optimization framework that subsumes such settings and several existing methods like Local SGDA. We show that naive aggregation of heterogeneous local progress results in optimizing a mismatched objective function -- a phenomenon previously observed in standard federated minimization. To fix this problem, we propose normalizing the client updates by the number of local steps undertaken between successive communication rounds. We analyze the convergence of the proposed algorithm for classes of nonconvex-concave and nonconvex-nonconcave functions and characterize the impact of heterogeneous client data, partial client participation, and heterogeneous local computations. Our analysis works under more general assumptions on the intra-client noise and inter-client heterogeneity than so far considered in the literature. For all the function classes considered, we significantly improve the existing computation and communication complexity results. Experimental results support our theoretical claims.

On the Convergence of Federated Averaging with Cyclic Client Participation

Federated Averaging (FedAvg) and its variants are the most popular optimization algorithms in federated learning (FL). Previous convergence analyses of FedAvg either assume full client participation or partial client participation where the clients can be uniformly sampled. However, in practical cross-device FL systems, only a subset of clients that satisfy local criteria such as battery status, network connectivity, and maximum participation frequency requirements (to ensure privacy) are available for training at a given time. As a result, client availability follows a natural cyclic pattern. We provide (to our knowledge) the first theoretical framework to analyze the convergence of FedAvg with cyclic client participation with several different client optimizers such as GD, SGD, and shuffled SGD. Our analysis discovers that cyclic client participation can achieve a faster asymptotic convergence rate than vanilla FedAvg with uniform client participation under suitable conditions, providing valuable insights into the design of client sampling protocols.

FedVARP: Tackling the Variance Due to Partial Client Participation in Federated Learning

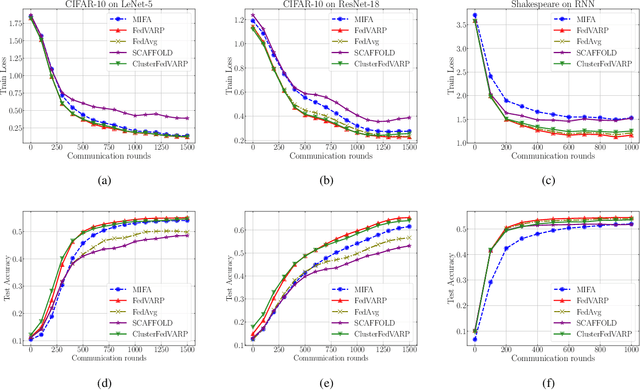
Data-heterogeneous federated learning (FL) systems suffer from two significant sources of convergence error: 1) client drift error caused by performing multiple local optimization steps at clients, and 2) partial client participation error caused by the fact that only a small subset of the edge clients participate in every training round. We find that among these, only the former has received significant attention in the literature. To remedy this, we propose FedVARP, a novel variance reduction algorithm applied at the server that eliminates error due to partial client participation. To do so, the server simply maintains in memory the most recent update for each client and uses these as surrogate updates for the non-participating clients in every round. Further, to alleviate the memory requirement at the server, we propose a novel clustering-based variance reduction algorithm ClusterFedVARP. Unlike previously proposed methods, both FedVARP and ClusterFedVARP do not require additional computation at clients or communication of additional optimization parameters. Through extensive experiments, we show that FedVARP outperforms state-of-the-art methods, and ClusterFedVARP achieves performance comparable to FedVARP with much less memory requirements.

Federated Reinforcement Learning: Linear Speedup Under Markovian Sampling

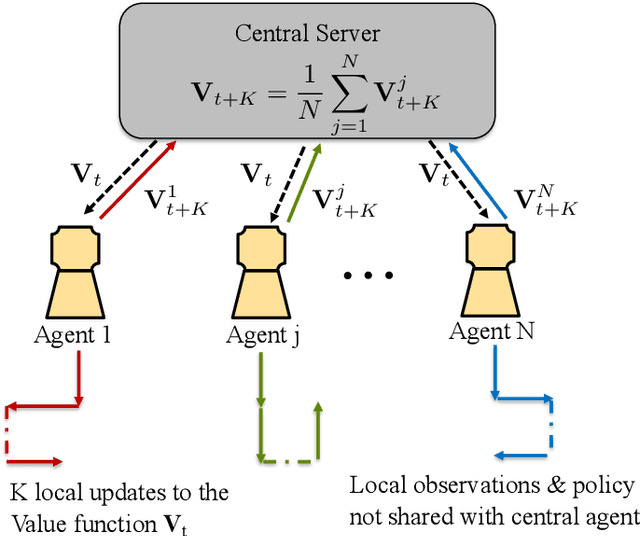
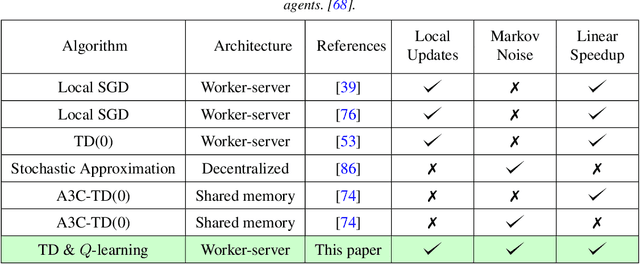
Since reinforcement learning algorithms are notoriously data-intensive, the task of sampling observations from the environment is usually split across multiple agents. However, transferring these observations from the agents to a central location can be prohibitively expensive in terms of the communication cost, and it can also compromise the privacy of each agent's local behavior policy. In this paper, we consider a federated reinforcement learning framework where multiple agents collaboratively learn a global model, without sharing their individual data and policies. Each agent maintains a local copy of the model and updates it using locally sampled data. Although having N agents enables the sampling of N times more data, it is not clear if it leads to proportional convergence speedup. We propose federated versions of on-policy TD, off-policy TD and Q-learning, and analyze their convergence. For all these algorithms, to the best of our knowledge, we are the first to consider Markovian noise and multiple local updates, and prove a linear convergence speedup with respect to the number of agents. To obtain these results, we show that federated TD and Q-learning are special cases of a general framework for federated stochastic approximation with Markovian noise, and we leverage this framework to provide a unified convergence analysis that applies to all the algorithms.

Distributed Estimation in Large Scale Wireless Sensor Networks via a Two Step Group-based Approach

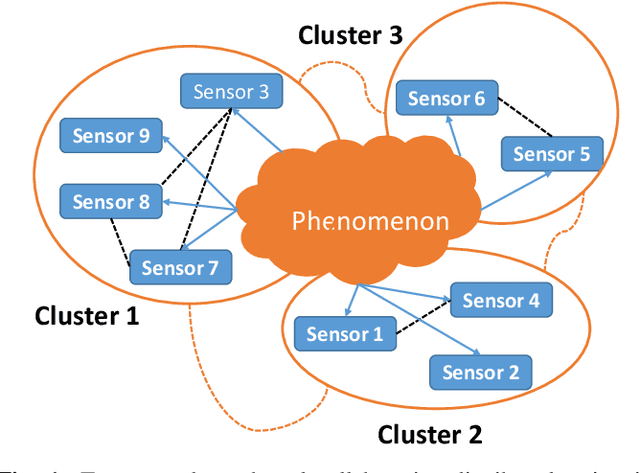
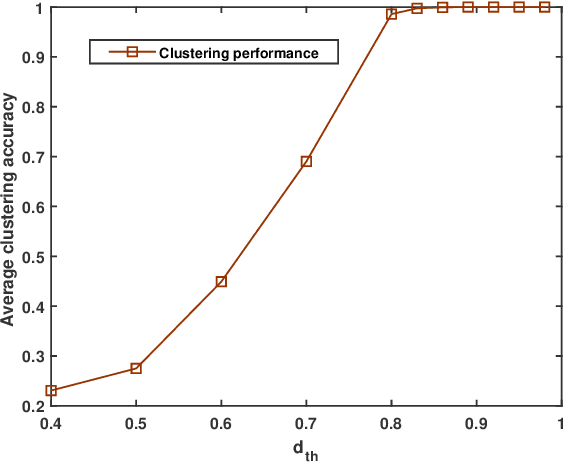
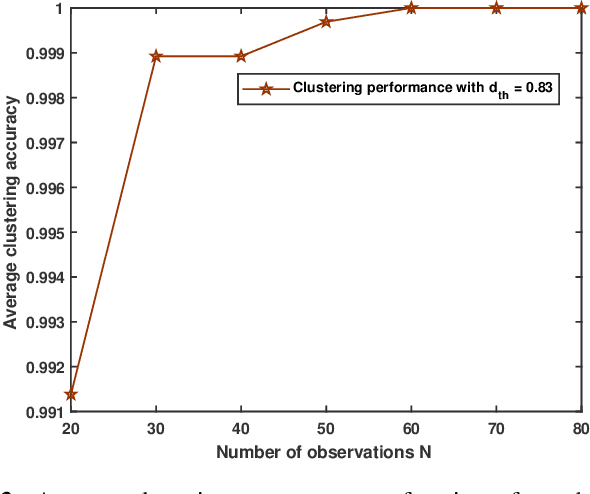
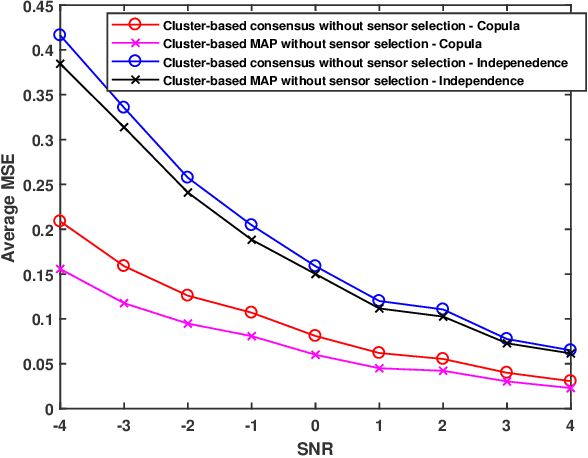
We consider the problem of collaborative distributed estimation in a large scale sensor network with statistically dependent sensor observations. In collaborative setup, the aim is to maximize the overall estimation performance by modeling the underlying statistical dependence and efficiently utilizing the deployed sensors. To achieve greater sensor transmission and estimation efficiency, we propose a two step group-based collaborative distributed estimation scheme, where in the first step, sensors form dependence driven groups such that sensors in the same group are highly dependent, while sensors from different groups are independent, and perform a copula-based maximum a posteriori probability (MAP) estimation via intragroup collaboration. In the second step, the estimates generated in the first step are shared via inter-group collaboration to reach an average consensus. A merge based K-medoid dependence driven grouping algorithm is proposed. Moreover, we further propose a group-based sensor selection scheme using mutual information prior to the estimation. The aim is to select sensors with maximum relevance and minimum redundancy regarding the parameter of interest under certain pre-specified energy constraint. Also, the proposed group-based sensor selection scheme is shown to be equivalent to the global/non-group based selection scheme with high probability, but computationally more efficient. Numerical experiments are conducted to demonstrate the effectiveness of our approach.

Federated Minimax Optimization: Improved Convergence Analyses and Algorithms

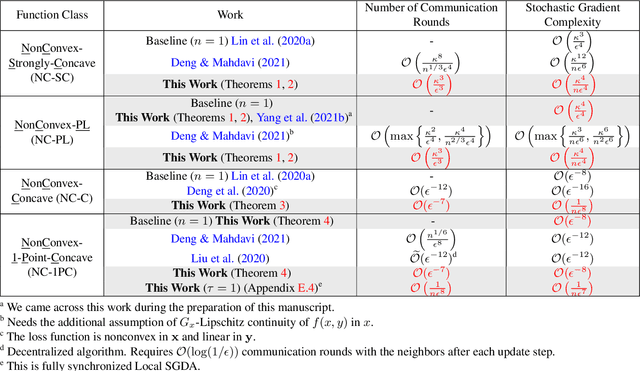
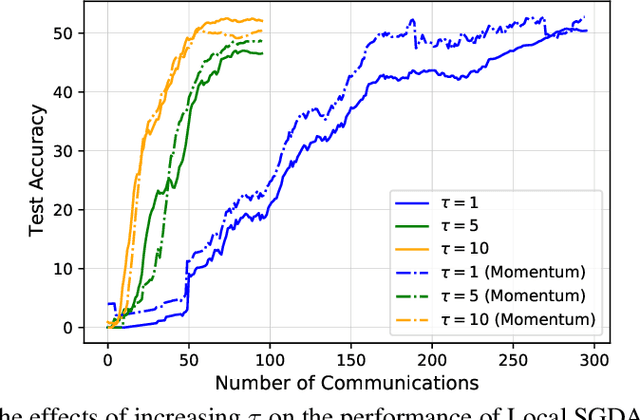
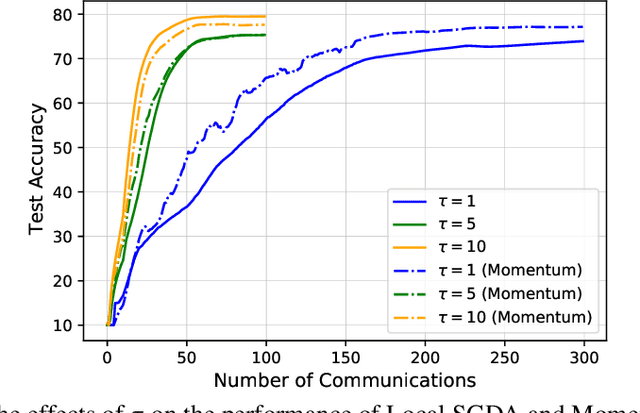
In this paper, we consider nonconvex minimax optimization, which is gaining prominence in many modern machine learning applications such as GANs. Large-scale edge-based collection of training data in these applications calls for communication-efficient distributed optimization algorithms, such as those used in federated learning, to process the data. In this paper, we analyze Local stochastic gradient descent ascent (SGDA), the local-update version of the SGDA algorithm. SGDA is the core algorithm used in minimax optimization, but it is not well-understood in a distributed setting. We prove that Local SGDA has \textit{order-optimal} sample complexity for several classes of nonconvex-concave and nonconvex-nonconcave minimax problems, and also enjoys \textit{linear speedup} with respect to the number of clients. We provide a novel and tighter analysis, which improves the convergence and communication guarantees in the existing literature. For nonconvex-PL and nonconvex-one-point-concave functions, we improve the existing complexity results for centralized minimax problems. Furthermore, we propose a momentum-based local-update algorithm, which has the same convergence guarantees, but outperforms Local SGDA as demonstrated in our experiments.

STEM: A Stochastic Two-Sided Momentum Algorithm Achieving Near-Optimal Sample and Communication Complexities for Federated Learning

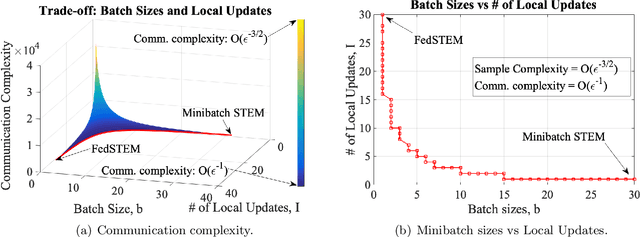
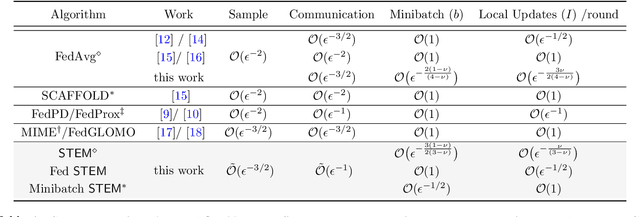
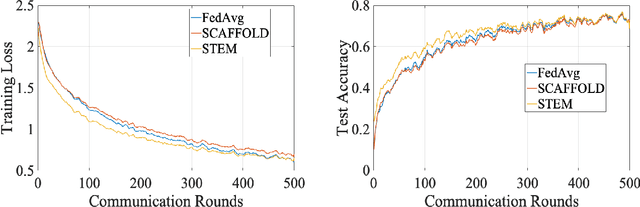
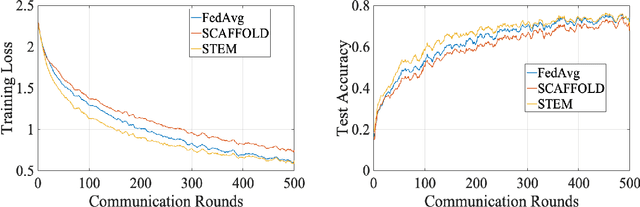
Federated Learning (FL) refers to the paradigm where multiple worker nodes (WNs) build a joint model by using local data. Despite extensive research, for a generic non-convex FL problem, it is not clear, how to choose the WNs' and the server's update directions, the minibatch sizes, and the local update frequency, so that the WNs use the minimum number of samples and communication rounds to achieve the desired solution. This work addresses the above question and considers a class of stochastic algorithms where the WNs perform a few local updates before communication. We show that when both the WN's and the server's directions are chosen based on a stochastic momentum estimator, the algorithm requires $\tilde{\mathcal{O}}(\epsilon^{-3/2})$ samples and $\tilde{\mathcal{O}}(\epsilon^{-1})$ communication rounds to compute an $\epsilon$-stationary solution. To the best of our knowledge, this is the first FL algorithm that achieves such {\it near-optimal} sample and communication complexities simultaneously. Further, we show that there is a trade-off curve between local update frequencies and local minibatch sizes, on which the above sample and communication complexities can be maintained. Finally, we show that for the classical FedAvg (a.k.a. Local SGD, which is a momentum-less special case of the STEM), a similar trade-off curve exists, albeit with worse sample and communication complexities. Our insights on this trade-off provides guidelines for choosing the four important design elements for FL algorithms, the update frequency, directions, and minibatch sizes to achieve the best performance.

Zeroth-Order Hybrid Gradient Descent: Towards A Principled Black-Box Optimization Framework

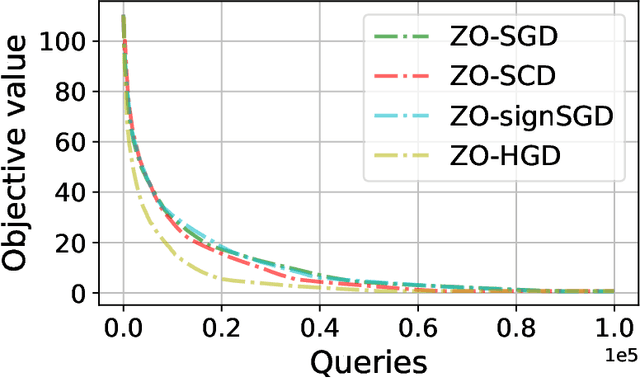
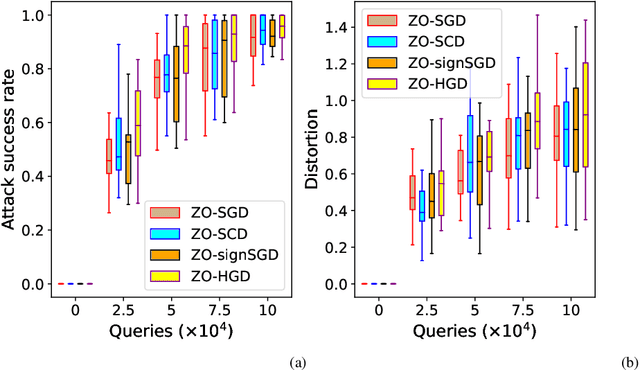
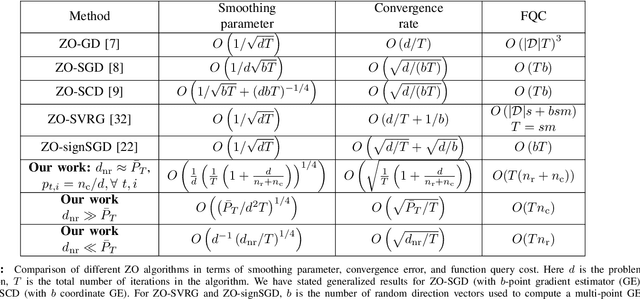
In this work, we focus on the study of stochastic zeroth-order (ZO) optimization which does not require first-order gradient information and uses only function evaluations. The problem of ZO optimization has emerged in many recent machine learning applications, where the gradient of the objective function is either unavailable or difficult to compute. In such cases, we can approximate the full gradients or stochastic gradients through function value based gradient estimates. Here, we propose a novel hybrid gradient estimator (HGE), which takes advantage of the query-efficiency of random gradient estimates as well as the variance-reduction of coordinate-wise gradient estimates. We show that with a graceful design in coordinate importance sampling, the proposed HGE-based ZO optimization method is efficient both in terms of iteration complexity as well as function query cost. We provide a thorough theoretical analysis of the convergence of our proposed method for non-convex, convex, and strongly-convex optimization. We show that the convergence rate that we derive generalizes the results for some prominent existing methods in the nonconvex case, and matches the optimal result in the convex case. We also corroborate the theory with a real-world black-box attack generation application to demonstrate the empirical advantage of our method over state-of-the-art ZO optimization approaches.