Microscaling Data Formats for Deep Learning

Narrow bit-width data formats are key to reducing the computational and storage costs of modern deep learning applications. This paper evaluates Microscaling (MX) data formats that combine a per-block scaling factor with narrow floating-point and integer types for individual elements. MX formats balance the competing needs of hardware efficiency, model accuracy, and user friction. Empirical results on over two dozen benchmarks demonstrate practicality of MX data formats as a drop-in replacement for baseline FP32 for AI inference and training with low user friction. We also show the first instance of training generative language models at sub-8-bit weights, activations, and gradients with minimal accuracy loss and no modifications to the training recipe.

FP8 Formats for Deep Learning

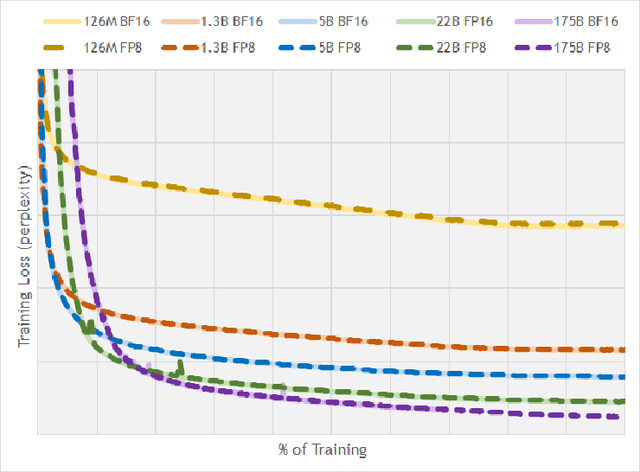
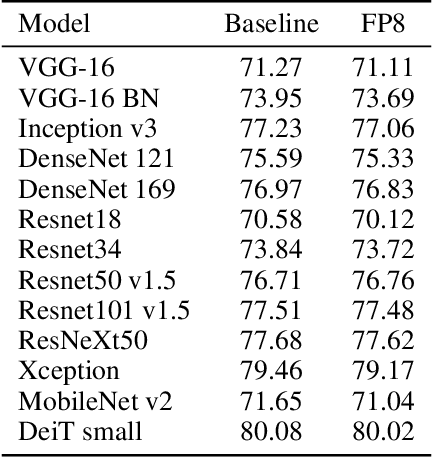
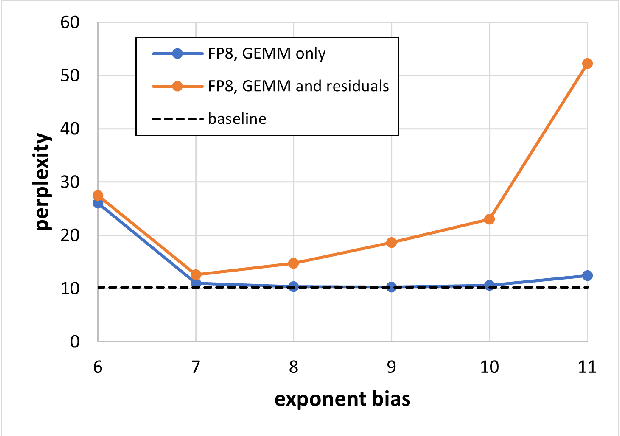
FP8 is a natural progression for accelerating deep learning training inference beyond the 16-bit formats common in modern processors. In this paper we propose an 8-bit floating point (FP8) binary interchange format consisting of two encodings - E4M3 (4-bit exponent and 3-bit mantissa) and E5M2 (5-bit exponent and 2-bit mantissa). While E5M2 follows IEEE 754 conventions for representatio of special values, E4M3's dynamic range is extended by not representing infinities and having only one mantissa bit-pattern for NaNs. We demonstrate the efficacy of the FP8 format on a variety of image and language tasks, effectively matching the result quality achieved by 16-bit training sessions. Our study covers the main modern neural network architectures - CNNs, RNNs, and Transformer-based models, leaving all the hyperparameters unchanged from the 16-bit baseline training sessions. Our training experiments include large, up to 175B parameter, language models. We also examine FP8 post-training-quantization of language models trained using 16-bit formats that resisted fixed point int8 quantization.

Accelerating Sparse Deep Neural Networks

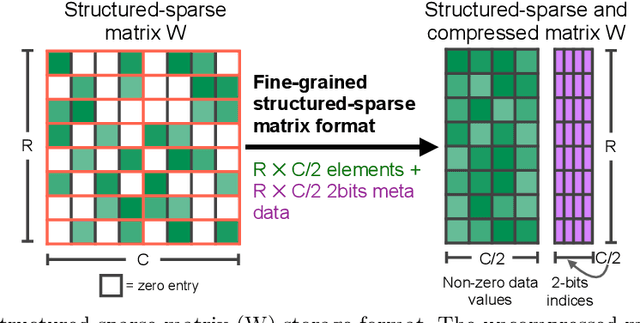
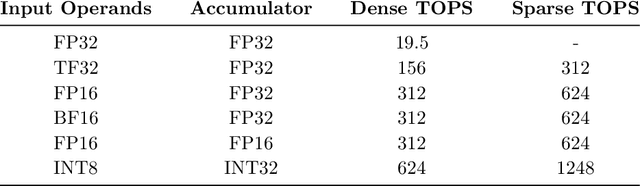
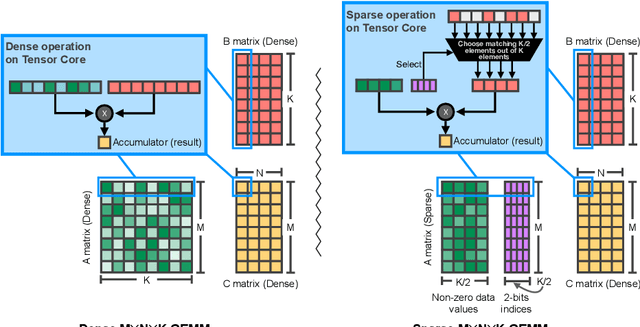
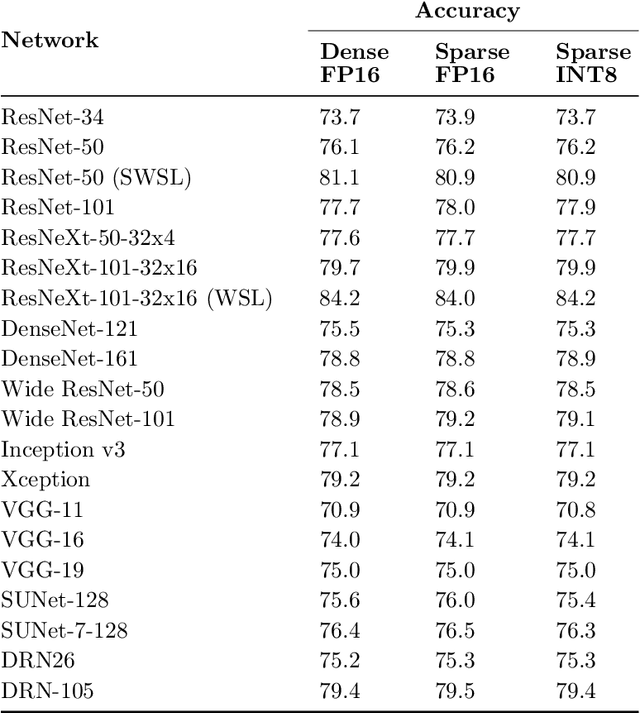
As neural network model sizes have dramatically increased, so has the interest in various techniques to reduce their parameter counts and accelerate their execution. An active area of research in this field is sparsity - encouraging zero values in parameters that can then be discarded from storage or computations. While most research focuses on high levels of sparsity, there are challenges in universally maintaining model accuracy as well as achieving significant speedups over modern matrix-math hardware. To make sparsity adoption practical, the NVIDIA Ampere GPU architecture introduces sparsity support in its matrix-math units, Tensor Cores. We present the design and behavior of Sparse Tensor Cores, which exploit a 2:4 (50%) sparsity pattern that leads to twice the math throughput of dense matrix units. We also describe a simple workflow for training networks that both satisfy 2:4 sparsity pattern requirements and maintain accuracy, verifying it on a wide range of common tasks and model architectures. This workflow makes it easy to prepare accurate models for efficient deployment on Sparse Tensor Cores.

Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation

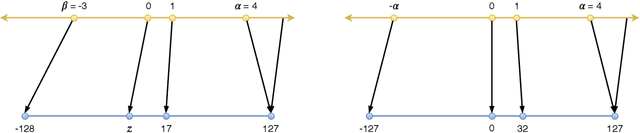
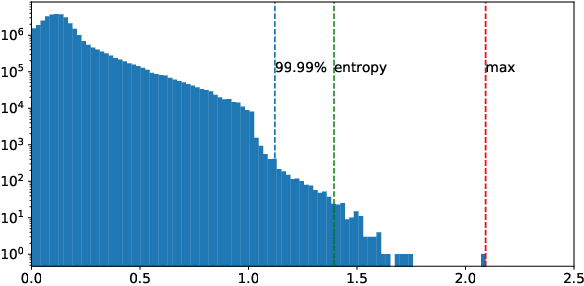
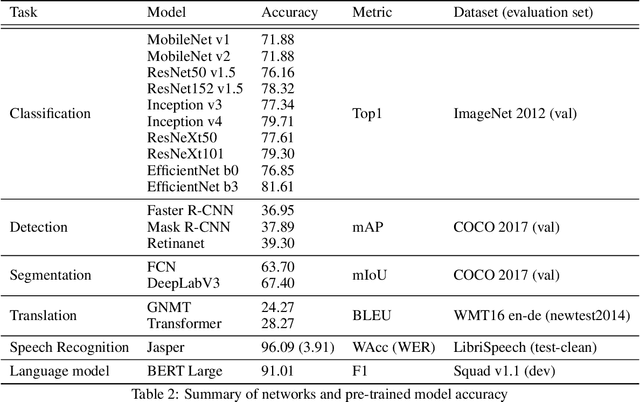
Quantization techniques can reduce the size of Deep Neural Networks and improve inference latency and throughput by taking advantage of high throughput integer instructions. In this paper we review the mathematical aspects of quantization parameters and evaluate their choices on a wide range of neural network models for different application domains, including vision, speech, and language. We focus on quantization techniques that are amenable to acceleration by processors with high-throughput integer math pipelines. We also present a workflow for 8-bit quantization that is able to maintain accuracy within 1% of the floating-point baseline on all networks studied, including models that are more difficult to quantize, such as MobileNets and BERT-large.

MLPerf Inference Benchmark

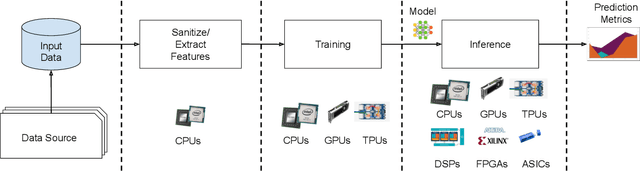
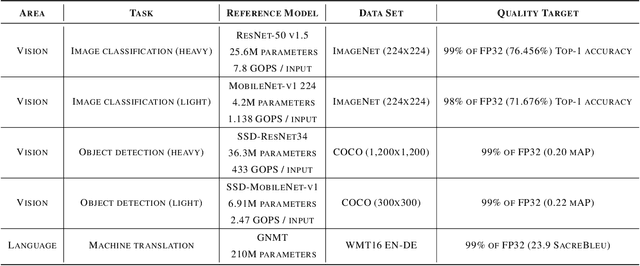
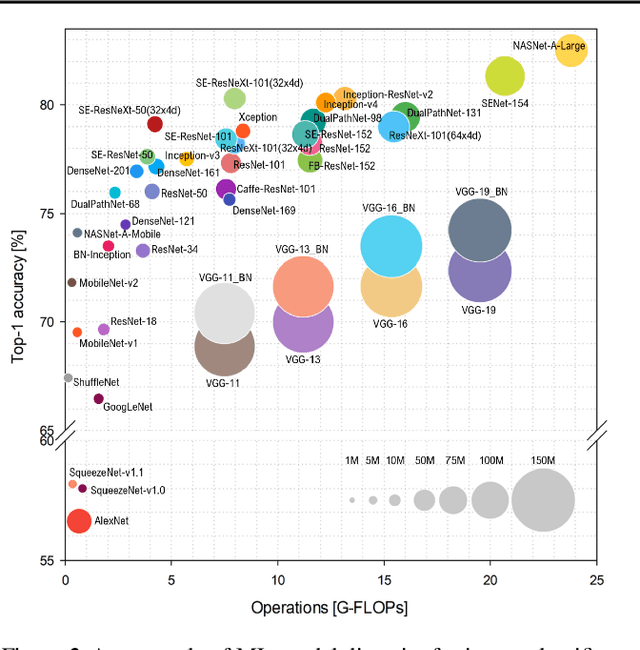
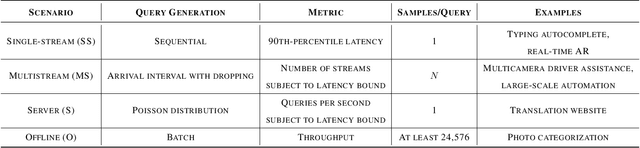
Machine-learning (ML) hardware and software system demand is burgeoning. Driven by ML applications, the number of different ML inference systems has exploded. Over 100 organizations are building ML inference chips, and the systems that incorporate existing models span at least three orders of magnitude in power consumption and four orders of magnitude in performance; they range from embedded devices to data-center solutions. Fueling the hardware are a dozen or more software frameworks and libraries. The myriad combinations of ML hardware and ML software make assessing ML-system performance in an architecture-neutral, representative, and reproducible manner challenging. There is a clear need for industry-wide standard ML benchmarking and evaluation criteria. MLPerf Inference answers that call. Driven by more than 30 organizations as well as more than 200 ML engineers and practitioners, MLPerf implements a set of rules and practices to ensure comparability across systems with wildly differing architectures. In this paper, we present the method and design principles of the initial MLPerf Inference release. The first call for submissions garnered more than 600 inference-performance measurements from 14 organizations, representing over 30 systems that show a range of capabilities.

MLPerf Training Benchmark

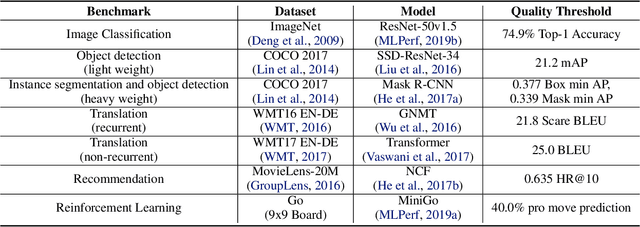
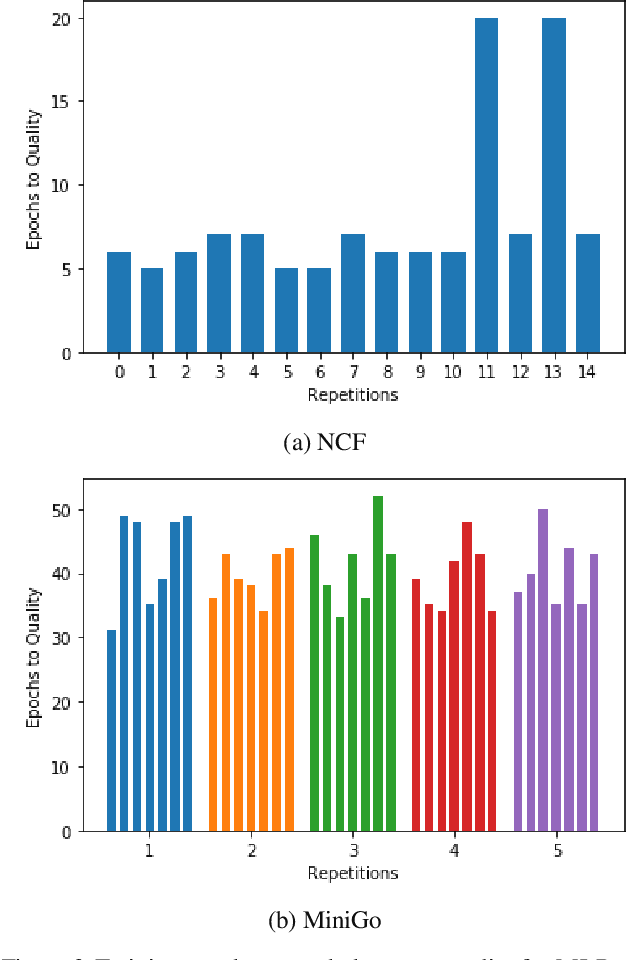
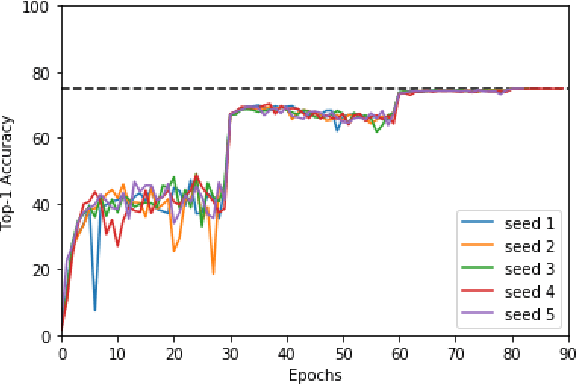
Machine learning is experiencing an explosion of software and hardware solutions, and needs industry-standard performance benchmarks to drive design and enable competitive evaluation. However, machine learning training presents a number of unique challenges to benchmarking that do not exist in other domains: (1) some optimizations that improve training throughput actually increase time to solution, (2) training is stochastic and time to solution has high variance, and (3) the software and hardware systems are so diverse that they cannot be fairly benchmarked with the same binary, code, or even hyperparameters. We present MLPerf, a machine learning benchmark that overcomes these challenges. We quantitatively evaluate the efficacy of MLPerf in driving community progress on performance and scalability across two rounds of results from multiple vendors.

OpenSeq2Seq: extensible toolkit for distributed and mixed precision training of sequence-to-sequence models

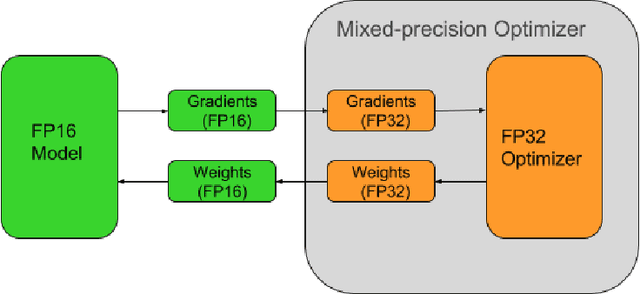
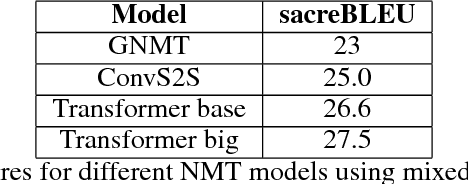
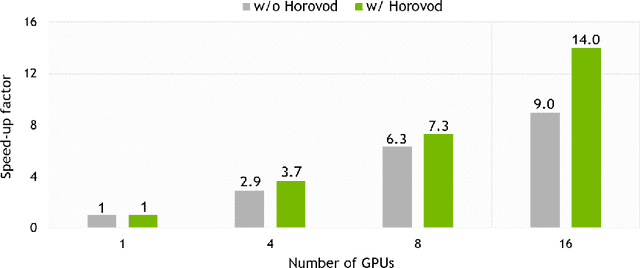
We present OpenSeq2Seq -- an open-source toolkit for training sequence-to-sequence models. The main goal of our toolkit is to allow researchers to most effectively explore different sequence-to-sequence architectures. The efficiency is achieved by fully supporting distributed and mixed-precision training. OpenSeq2Seq provides building blocks for training encoder-decoder models for neural machine translation and automatic speech recognition. We plan to extend it with other modalities in the future.

Mixed Precision Training

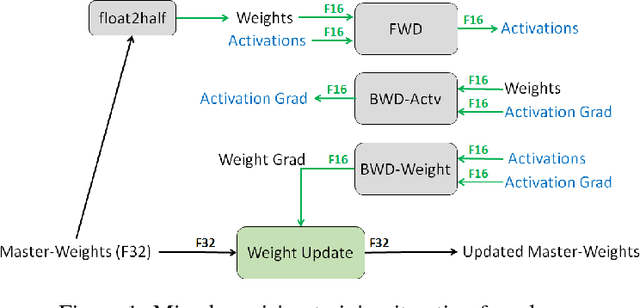
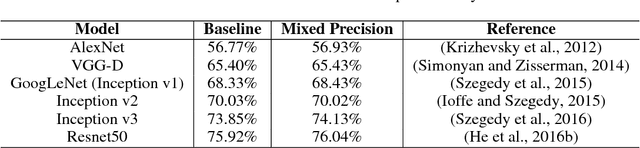
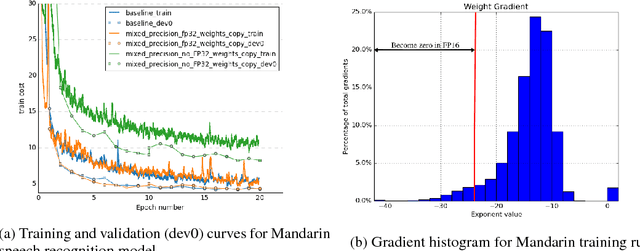
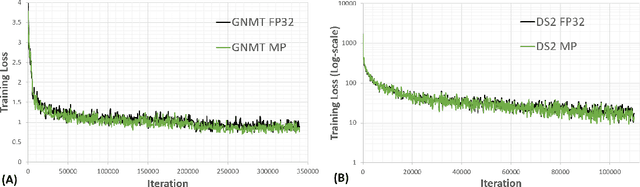
Deep neural networks have enabled progress in a wide variety of applications. Growing the size of the neural network typically results in improved accuracy. As model sizes grow, the memory and compute requirements for training these models also increases. We introduce a technique to train deep neural networks using half precision floating point numbers. In our technique, weights, activations and gradients are stored in IEEE half-precision format. Half-precision floating numbers have limited numerical range compared to single-precision numbers. We propose two techniques to handle this loss of information. Firstly, we recommend maintaining a single-precision copy of the weights that accumulates the gradients after each optimizer step. This single-precision copy is rounded to half-precision format during training. Secondly, we propose scaling the loss appropriately to handle the loss of information with half-precision gradients. We demonstrate that this approach works for a wide variety of models including convolution neural networks, recurrent neural networks and generative adversarial networks. This technique works for large scale models with more than 100 million parameters trained on large datasets. Using this approach, we can reduce the memory consumption of deep learning models by nearly 2x. In future processors, we can also expect a significant computation speedup using half-precision hardware units.