Discovering Order in Unordered Datasets: Generative Markov Networks

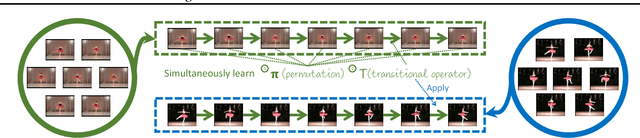
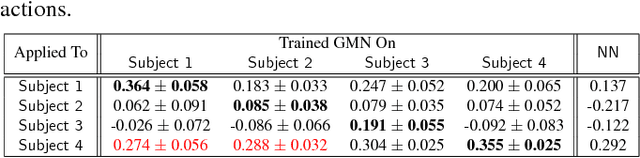
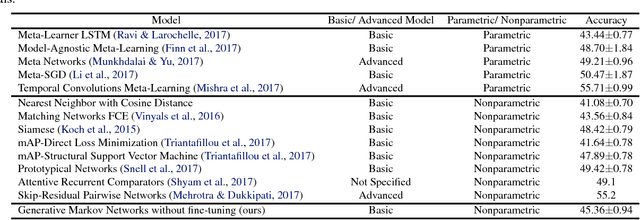
The assumption that data samples are independently identically distributed is the backbone of many learning algorithms. Nevertheless, datasets often exhibit rich structures in practice, and we argue that there exist some unknown orders within the data instances. Aiming to find such orders, we introduce a novel Generative Markov Network (GMN) which we use to extract the order of data instances automatically. Specifically, we assume that the instances are sampled from a Markov chain. Our goal is to learn the transitional operator of the chain as well as the generation order by maximizing the generation probability under all possible data permutations. One of our key ideas is to use neural networks as a soft lookup table for approximating the possibly huge, but discrete transition matrix. This strategy allows us to amortize the space complexity with a single model and make the transitional operator generalizable to unseen instances. To ensure the learned Markov chain is ergodic, we propose a greedy batch-wise permutation scheme that allows fast training. Empirically, we evaluate the learned Markov chain by showing that GMNs are able to discover orders among data instances and also perform comparably well to state-of-the-art methods on the one-shot recognition benchmark task.

Steering Output Style and Topic in Neural Response Generation

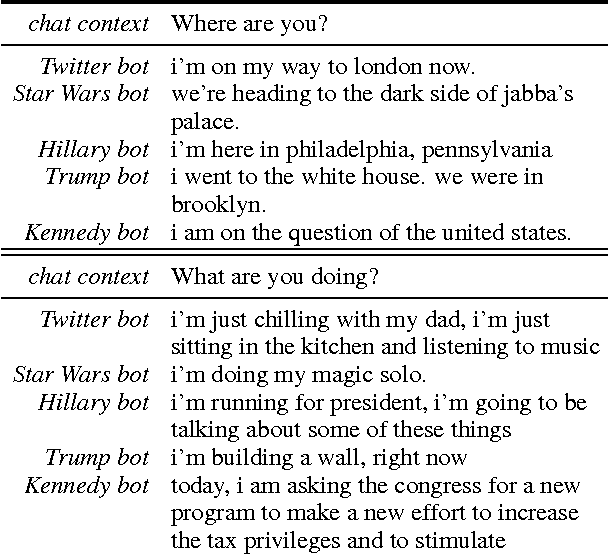
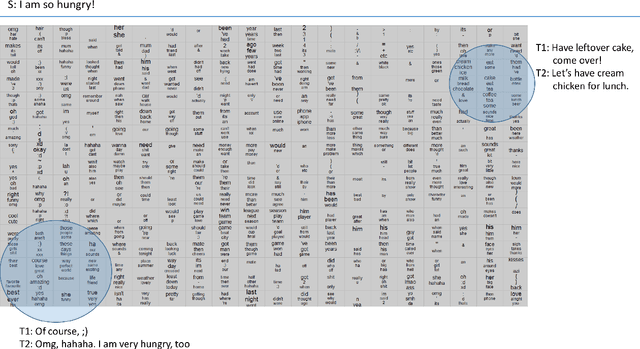
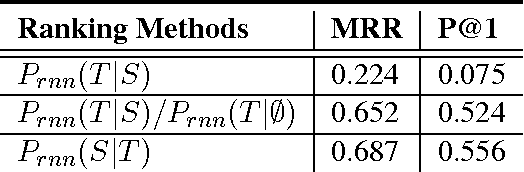
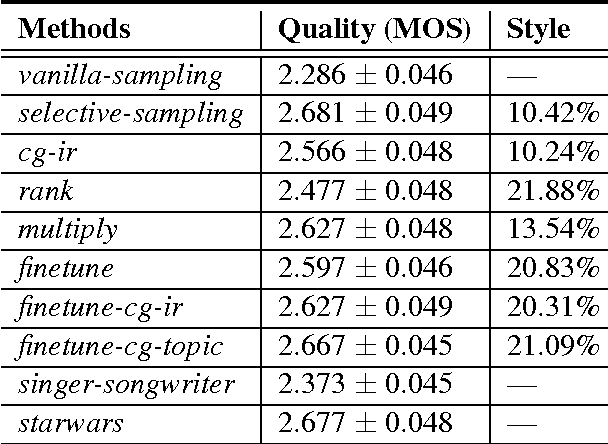
We propose simple and flexible training and decoding methods for influencing output style and topic in neural encoder-decoder based language generation. This capability is desirable in a variety of applications, including conversational systems, where successful agents need to produce language in a specific style and generate responses steered by a human puppeteer or external knowledge. We decompose the neural generation process into empirically easier sub-problems: a faithfulness model and a decoding method based on selective-sampling. We also describe training and sampling algorithms that bias the generation process with a specific language style restriction, or a topic restriction. Human evaluation results show that our proposed methods are able to restrict style and topic without degrading output quality in conversational tasks.

Discriminative Similarity for Clustering and Semi-Supervised Learning

Similarity-based clustering and semi-supervised learning methods separate the data into clusters or classes according to the pairwise similarity between the data, and the pairwise similarity is crucial for their performance. In this paper, we propose a novel discriminative similarity learning framework which learns discriminative similarity for either data clustering or semi-supervised learning. The proposed framework learns classifier from each hypothetical labeling, and searches for the optimal labeling by minimizing the generalization error of the learned classifiers associated with the hypothetical labeling. Kernel classifier is employed in our framework. By generalization analysis via Rademacher complexity, the generalization error bound for the kernel classifier learned from hypothetical labeling is expressed as the sum of pairwise similarity between the data from different classes, parameterized by the weights of the kernel classifier. Such pairwise similarity serves as the discriminative similarity for the purpose of clustering and semi-supervised learning, and discriminative similarity with similar form can also be induced by the integrated squared error bound for kernel density classification. Based on the discriminative similarity induced by the kernel classifier, we propose new clustering and semi-supervised learning methods.

On the Suboptimality of Proximal Gradient Descent for $\ell^{0}$ Sparse Approximation

We study the proximal gradient descent (PGD) method for $\ell^{0}$ sparse approximation problem as well as its accelerated optimization with randomized algorithms in this paper. We first offer theoretical analysis of PGD showing the bounded gap between the sub-optimal solution by PGD and the globally optimal solution for the $\ell^{0}$ sparse approximation problem under conditions weaker than Restricted Isometry Property widely used in compressive sensing literature. Moreover, we propose randomized algorithms to accelerate the optimization by PGD using randomized low rank matrix approximation (PGD-RMA) and randomized dimension reduction (PGD-RDR). Our randomized algorithms substantially reduces the computation cost of the original PGD for the $\ell^{0}$ sparse approximation problem, and the resultant sub-optimal solution still enjoys provable suboptimality, namely, the sub-optimal solution to the reduced problem still has bounded gap to the globally optimal solution to the original problem.

Hierarchical learning of grids of microtopics

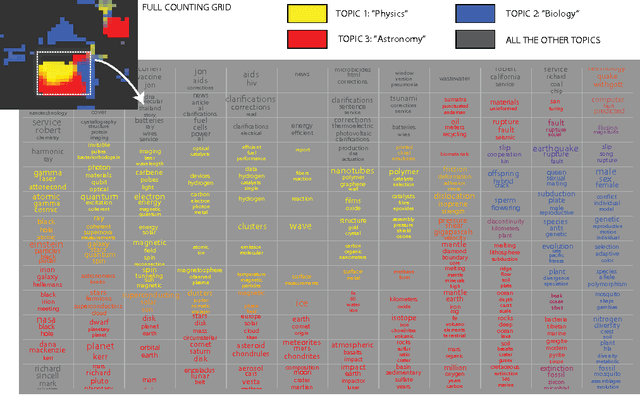
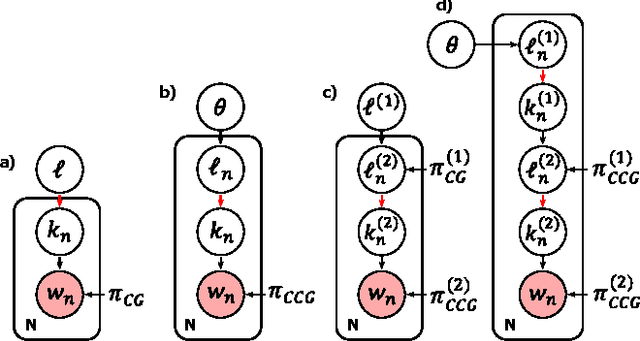
The counting grid is a grid of microtopics, sparse word/feature distributions. The generative model associated with the grid does not use these microtopics individually. Rather, it groups them in overlapping rectangular windows and uses these grouped microtopics as either mixture or admixture components. This paper builds upon the basic counting grid model and it shows that hierarchical reasoning helps avoid bad local minima, produces better classification accuracy and, most interestingly, allows for extraction of large numbers of coherent microtopics even from small datasets. We evaluate this in terms of consistency, diversity and clarity of the indexed content, as well as in a user study on word intrusion tasks. We demonstrate that these models work well as a technique for embedding raw images and discuss interesting parallels between hierarchical CG models and other deep architectures.

Capturing spatial interdependence in image features: the counting grid, an epitomic representation for bags of features

In recent scene recognition research images or large image regions are often represented as disorganized "bags" of features which can then be analyzed using models originally developed to capture co-variation of word counts in text. However, image feature counts are likely to be constrained in different ways than word counts in text. For example, as a camera pans upwards from a building entrance over its first few floors and then further up into the sky Fig. 1, some feature counts in the image drop while others rise -- only to drop again giving way to features found more often at higher elevations. The space of all possible feature count combinations is constrained both by the properties of the larger scene and the size and the location of the window into it. To capture such variation, in this paper we propose the use of the counting grid model. This generative model is based on a grid of feature counts, considerably larger than any of the modeled images, and considerably smaller than the real estate needed to tile the images next to each other tightly. Each modeled image is assumed to have a representative window in the grid in which the feature counts mimic the feature distribution in the image. We provide a learning procedure that jointly maps all images in the training set to the counting grid and estimates the appropriate local counts in it. Experimentally, we demonstrate that the resulting representation captures the space of feature count combinations more accurately than the traditional models, not only when the input images come from a panning camera, but even when modeling images of different scenes from the same category.

In the sight of my wearable camera: Classifying my visual experience

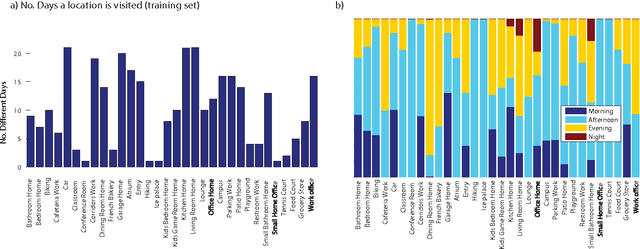
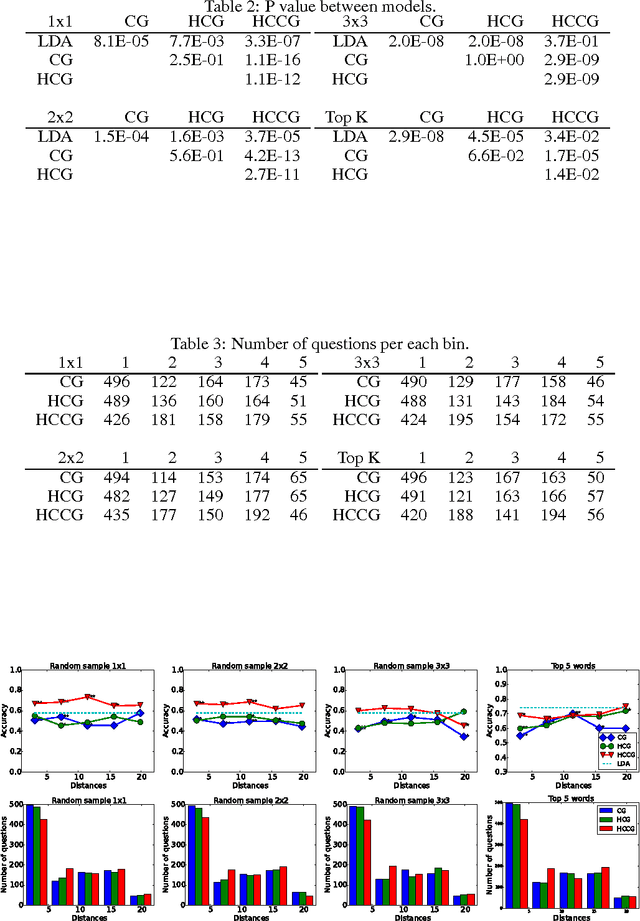
We introduce and we analyze a new dataset which resembles the input to biological vision systems much more than most previously published ones. Our analysis leaded to several important conclusions. First, it is possible to disambiguate over dozens of visual scenes (locations) encountered over the course of several weeks of a human life with accuracy of over 80%, and this opens up possibility for numerous novel vision applications, from early detection of dementia to everyday use of wearable camera streams for automatic reminders, and visual stream exchange. Second, our experimental results indicate that, generative models such as Latent Dirichlet Allocation or Counting Grids, are more suitable to such types of data, as they are more robust to overtraining and comfortable with images at low resolution, blurred and characterized by relatively random clutter and a mix of objects.

Learning Graphical Models of Images, Videos and Their Spatial Transformations

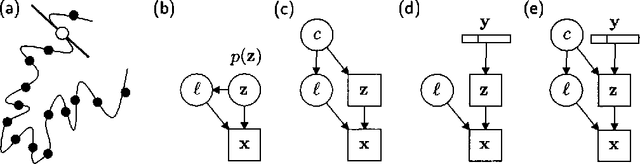
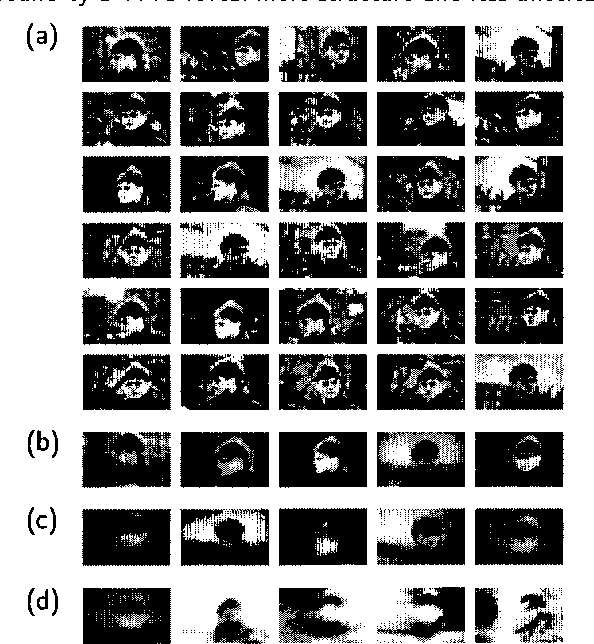
Mixtures of Gaussians, factor analyzers (probabilistic PCA) and hidden Markov models are staples of static and dynamic data modeling and image and video modeling in particular. We show how topographic transformations in the input, such as translation and shearing in images, can be accounted for in these models by including a discrete transformation variable. The resulting models perform clustering, dimensionality reduction and time-series analysis in a way that is invariant to transformations in the input. Using the EM algorithm, these transformation-invariant models can be fit to static data and time series. We give results on filtering microscopy images, face and facial pose clustering, handwritten digit modeling and recognition, video clustering, object tracking, and removal of distractions from video sequences.

Probabilistic index maps for modeling natural signals

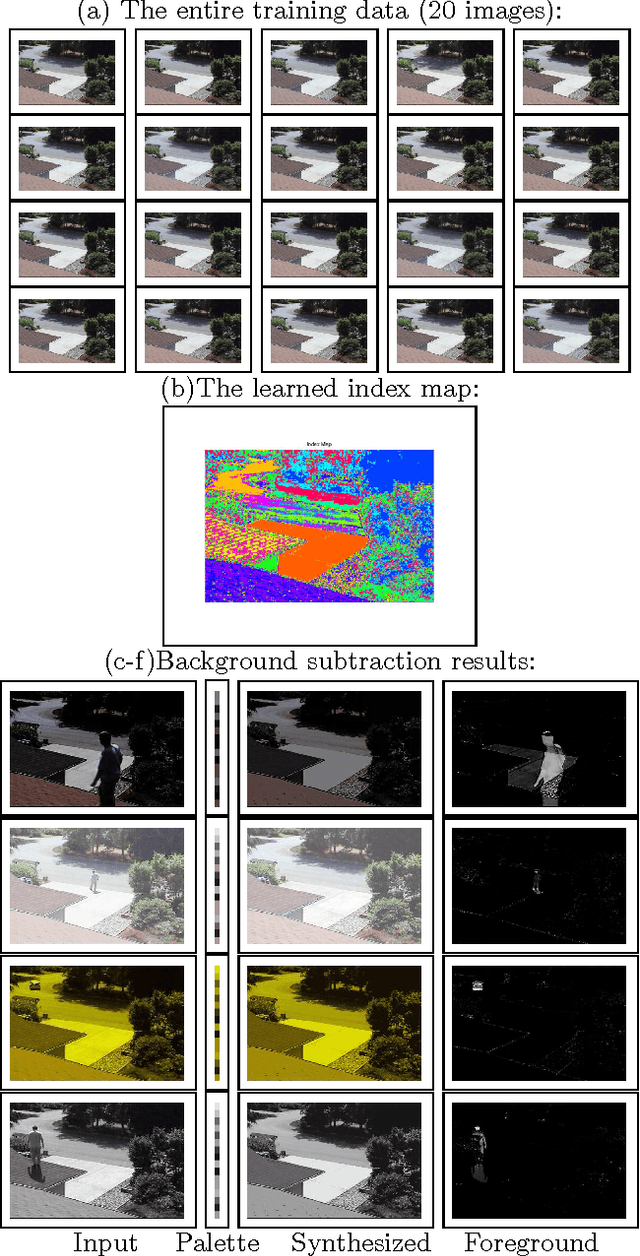
One of the major problems in modeling natural signals is that signals with very similar structure may locally have completely different measurements, e.g., images taken under different illumination conditions, or the speech signal captured in different environments. While there have been many successful attempts to address these problems in application-specific settings, we believe that underlying a large set of problems in signal representation is a representational deficiency of intensity-derived local measurements that are the basis of most efficient models. We argue that interesting structure in signals is better captured when the signal is de- fined as a matrix whose entries are discrete indices to a separate palette of possible measurements. In order to model the variability in signal structure, we define a signal class not by a single index map, but by a probability distribution over the index maps, which can be estimated from the data, and which we call probabilistic index maps. The existing algorithm can be adapted to work with this representation. Furthermore, the probabilistic index map representation leads to algorithms with computational costs proportional to either the size of the palette or the log of the size of the palette, making the cost of significantly increased invariance to non-structural changes quite bearable. We illustrate the benefits of the probabilistic index map representation in several applications in computer vision and speech processing.

Discovering Patterns in Biological Sequences by Optimal Segmentation

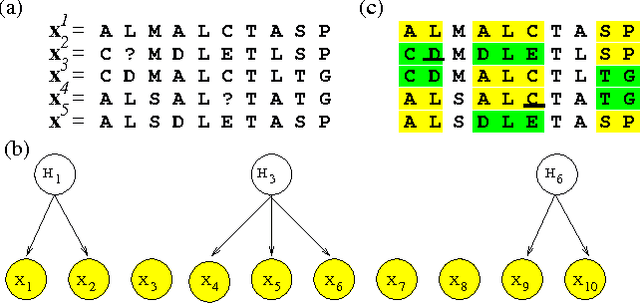
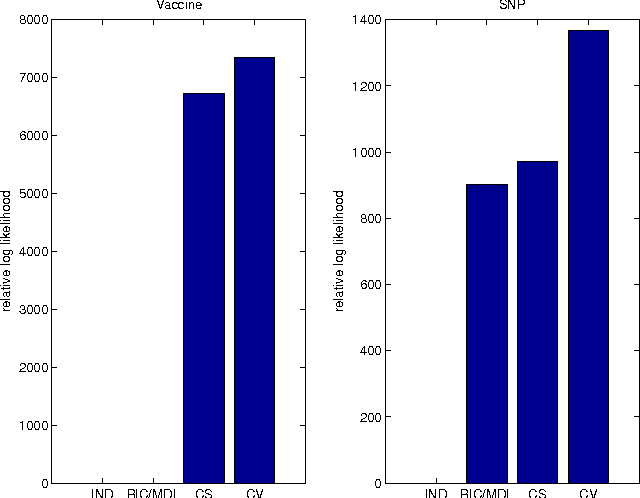
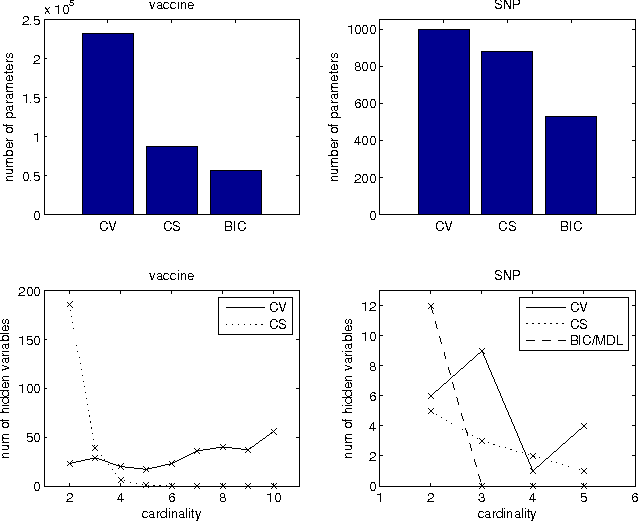
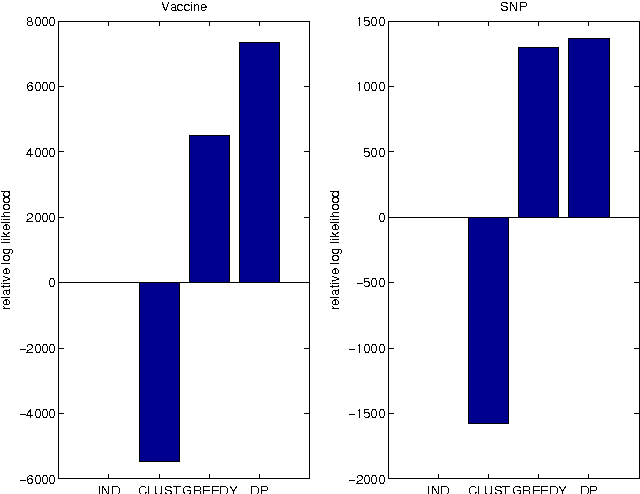
Computational methods for discovering patterns of local correlations in sequences are important in computational biology. Here we show how to determine the optimal partitioning of aligned sequences into non-overlapping segments such that positions in the same segment are strongly correlated while positions in different segments are not. Our approach involves discovering the hidden variables of a Bayesian network that interact with observed sequences so as to form a set of independent mixture models. We introduce a dynamic program to efficiently discover the optimal segmentation, or equivalently the optimal set of hidden variables. We evaluate our approach on two computational biology tasks. One task is related to the design of vaccines against polymorphic pathogens and the other task involves analysis of single nucleotide polymorphisms (SNPs) in human DNA. We show how common tasks in these problems naturally correspond to inference procedures in the learned models. Error rates of our learned models for the prediction of missing SNPs are up to 1/3 less than the error rates of a state-of-the-art SNP prediction method. Source code is available at www.uwm.edu/~joebock/segmentation.