Training Transformers with Enforced Lipschitz Constants

Neural networks are often highly sensitive to input and weight perturbations. This sensitivity has been linked to pathologies such as vulnerability to adversarial examples, divergent training, and overfitting. To combat these problems, past research has looked at building neural networks entirely from Lipschitz components. However, these techniques have not matured to the point where researchers have trained a modern architecture such as a transformer with a Lipschitz certificate enforced beyond initialization. To explore this gap, we begin by developing and benchmarking novel, computationally-efficient tools for maintaining norm-constrained weight matrices. Applying these tools, we are able to train transformer models with Lipschitz bounds enforced throughout training. We find that optimizer dynamics matter: switching from AdamW to Muon improves standard methods -- weight decay and spectral normalization -- allowing models to reach equal performance with a lower Lipschitz bound. Inspired by Muon's update having a fixed spectral norm, we co-design a weight constraint method that improves the Lipschitz vs. performance tradeoff on MLPs and 2M parameter transformers. Our 2-Lipschitz transformer on Shakespeare text reaches validation accuracy 60%. Scaling to 145M parameters, our 10-Lipschitz transformer reaches 21% accuracy on internet text. However, to match the NanoGPT baseline validation accuracy of 39.4%, our Lipschitz upper bound increases to 10^264. Nonetheless, our Lipschitz transformers train without stability measures such as layer norm, QK norm, and logit tanh softcapping.

Modular Duality in Deep Learning

An old idea in optimization theory says that since the gradient is a dual vector it may not be subtracted from the weights without first being mapped to the primal space where the weights reside. We take this idea seriously in this paper and construct such a duality map for general neural networks. Our map, which we call modular dualization, forms a unifying theoretical basis for training algorithms that are a) fast and b) scalable. Modular dualization involves first assigning operator norms to layers based on the semantics of each layer, and then using these layerwise norms to recursively induce a duality map on the weight space of the full neural architecture. We conclude by deriving GPU-friendly algorithms for dualizing Embed, Linear and Conv2D layers -- the latter two methods are based on a new rectangular Newton-Schulz iteration that we propose. Our iteration was recently used to set new speed records for training NanoGPT. Overall, we hope that our theory of modular duality will yield a next generation of fast and scalable optimizers for general neural architectures.

Old Optimizer, New Norm: An Anthology

Deep learning optimizers are often motivated through a mix of convex and approximate second-order theory. We select three such methods -- Adam, Shampoo and Prodigy -- and argue that each method can instead be understood as a squarely first-order method without convexity assumptions. In fact, after switching off exponential moving averages, each method is equivalent to steepest descent under a particular norm. By generalizing this observation, we chart a new design space for training algorithms. Different operator norms should be assigned to different tensors based on the role that the tensor plays within the network. For example, while linear and embedding layers may have the same weight space of $\mathbb{R}^{m\times n}$, these layers play different roles and should be assigned different norms. We hope that this idea of carefully metrizing the neural architecture might lead to more stable, scalable and indeed faster training.

Scalable Optimization in the Modular Norm

To improve performance in contemporary deep learning, one is interested in scaling up the neural network in terms of both the number and the size of the layers. When ramping up the width of a single layer, graceful scaling of training has been linked to the need to normalize the weights and their updates in the "natural norm" particular to that layer. In this paper, we significantly generalize this idea by defining the modular norm, which is the natural norm on the full weight space of any neural network architecture. The modular norm is defined recursively in tandem with the network architecture itself. We show that the modular norm has several promising applications. On the practical side, the modular norm can be used to normalize the updates of any base optimizer so that the learning rate becomes transferable across width and depth. This means that the user does not need to compute optimizer-specific scale factors in order to scale training. On the theoretical side, we show that for any neural network built from "well-behaved" atomic modules, the gradient of the network is Lipschitz-continuous in the modular norm, with the Lipschitz constant admitting a simple recursive formula. This characterization opens the door to porting standard ideas in optimization theory over to deep learning. We have created a Python package called Modula that automatically normalizes weight updates in the modular norm of the architecture. The package is available via "pip install modula" with source code at https://github.com/jxbz/modula.

Training Neural Networks from Scratch with Parallel Low-Rank Adapters

The scalability of deep learning models is fundamentally limited by computing resources, memory, and communication. Although methods like low-rank adaptation (LoRA) have reduced the cost of model finetuning, its application in model pre-training remains largely unexplored. This paper explores extending LoRA to model pre-training, identifying the inherent constraints and limitations of standard LoRA in this context. We introduce LoRA-the-Explorer (LTE), a novel bi-level optimization algorithm designed to enable parallel training of multiple low-rank heads across computing nodes, thereby reducing the need for frequent synchronization. Our approach includes extensive experimentation on vision transformers using various vision datasets, demonstrating that LTE is competitive with standard pre-training.

A Spectral Condition for Feature Learning

The push to train ever larger neural networks has motivated the study of initialization and training at large network width. A key challenge is to scale training so that a network's internal representations evolve nontrivially at all widths, a process known as feature learning. Here, we show that feature learning is achieved by scaling the spectral norm of weight matrices and their updates like $\sqrt{\texttt{fan-out}/\texttt{fan-in}}$, in contrast to widely used but heuristic scalings based on Frobenius norm and entry size. Our spectral scaling analysis also leads to an elementary derivation of \emph{maximal update parametrization}. All in all, we aim to provide the reader with a solid conceptual understanding of feature learning in neural networks.

SketchOGD: Memory-Efficient Continual Learning

When machine learning models are trained continually on a sequence of tasks, they are liable to forget what they learned on previous tasks -- a phenomenon known as catastrophic forgetting. Proposed solutions to catastrophic forgetting tend to involve storing information about past tasks, meaning that memory usage is a chief consideration in determining their practicality. This paper proposes a memory-efficient solution to catastrophic forgetting, improving upon an established algorithm known as orthogonal gradient descent (OGD). OGD utilizes prior model gradients to find weight updates that preserve performance on prior datapoints. However, since the memory cost of storing prior model gradients grows with the runtime of the algorithm, OGD is ill-suited to continual learning over arbitrarily long time horizons. To address this problem, this paper proposes SketchOGD. SketchOGD employs an online sketching algorithm to compress model gradients as they are encountered into a matrix of a fixed, user-determined size. In contrast to existing memory-efficient variants of OGD, SketchOGD runs online without the need for advance knowledge of the total number of tasks, is simple to implement, and is more amenable to analysis. We provide theoretical guarantees on the approximation error of the relevant sketches under a novel metric suited to the downstream task of OGD. Experimentally, we find that SketchOGD tends to outperform current state-of-the-art variants of OGD given a fixed memory budget.

Automatic Gradient Descent: Deep Learning without Hyperparameters

The architecture of a deep neural network is defined explicitly in terms of the number of layers, the width of each layer and the general network topology. Existing optimisation frameworks neglect this information in favour of implicit architectural information (e.g. second-order methods) or architecture-agnostic distance functions (e.g. mirror descent). Meanwhile, the most popular optimiser in practice, Adam, is based on heuristics. This paper builds a new framework for deriving optimisation algorithms that explicitly leverage neural architecture. The theory extends mirror descent to non-convex composite objective functions: the idea is to transform a Bregman divergence to account for the non-linear structure of neural architecture. Working through the details for deep fully-connected networks yields automatic gradient descent: a first-order optimiser without any hyperparameters. Automatic gradient descent trains both fully-connected and convolutional networks out-of-the-box and at ImageNet scale. A PyTorch implementation is available at https://github.com/jxbz/agd and also in Appendix B. Overall, the paper supplies a rigorous theoretical foundation for a next-generation of architecture-dependent optimisers that work automatically and without hyperparameters.

Optimisation & Generalisation in Networks of Neurons

The goal of this thesis is to develop the optimisation and generalisation theoretic foundations of learning in artificial neural networks. On optimisation, a new theoretical framework is proposed for deriving architecture-dependent first-order optimisation algorithms. The approach works by combining a "functional majorisation" of the loss function with "architectural perturbation bounds" that encode an explicit dependence on neural architecture. The framework yields optimisation methods that transfer hyperparameters across learning problems. On generalisation, a new correspondence is proposed between ensembles of networks and individual networks. It is argued that, as network width and normalised margin are taken large, the space of networks that interpolate a particular training set concentrates on an aggregated Bayesian method known as a "Bayes point machine". This correspondence provides a route for transferring PAC-Bayesian generalisation theorems over to individual networks. More broadly, the correspondence presents a fresh perspective on the role of regularisation in networks with vastly more parameters than data.

Investigating Generalization by Controlling Normalized Margin

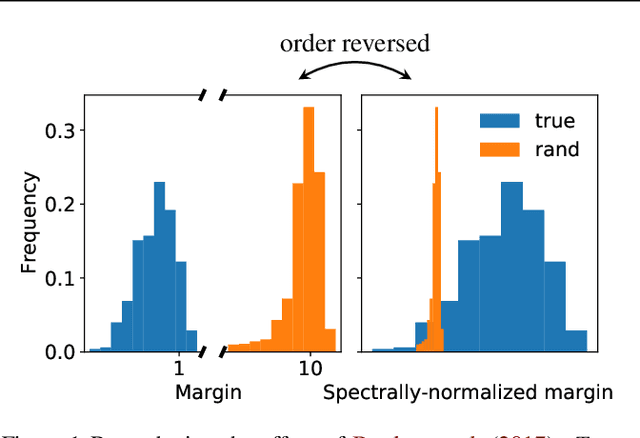
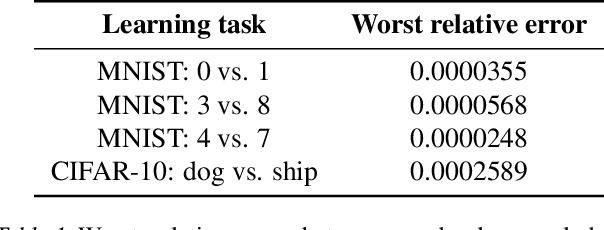
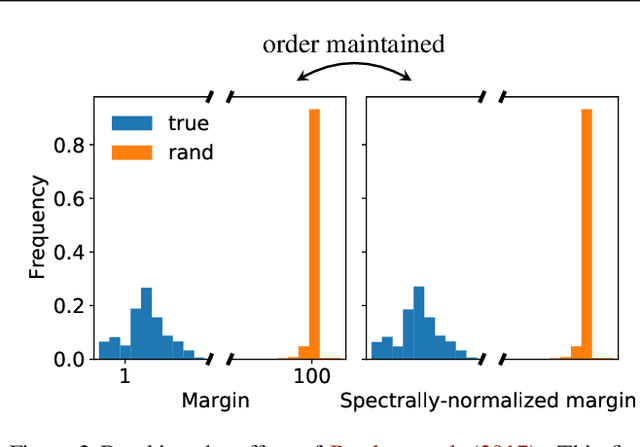
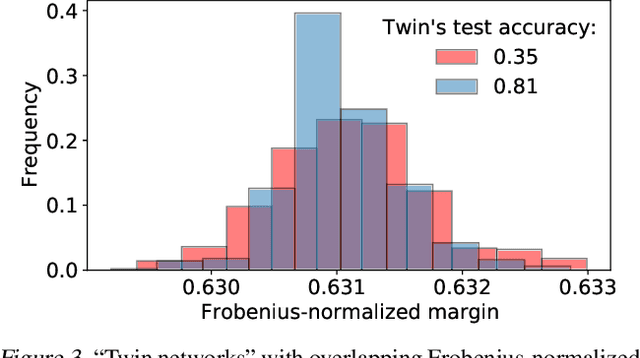
Weight norm $\|w\|$ and margin $\gamma$ participate in learning theory via the normalized margin $\gamma/\|w\|$. Since standard neural net optimizers do not control normalized margin, it is hard to test whether this quantity causally relates to generalization. This paper designs a series of experimental studies that explicitly control normalized margin and thereby tackle two central questions. First: does normalized margin always have a causal effect on generalization? The paper finds that no -- networks can be produced where normalized margin has seemingly no relationship with generalization, counter to the theory of Bartlett et al. (2017). Second: does normalized margin ever have a causal effect on generalization? The paper finds that yes -- in a standard training setup, test performance closely tracks normalized margin. The paper suggests a Gaussian process model as a promising explanation for this behavior.