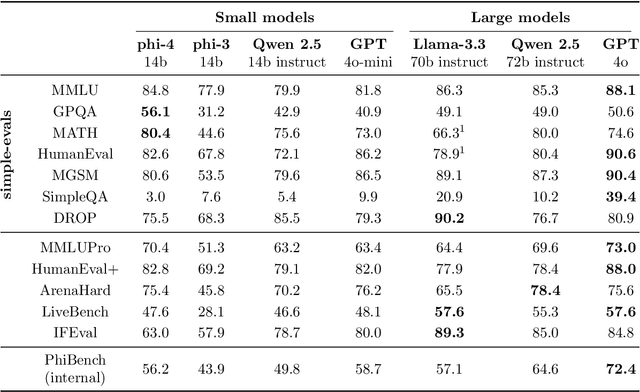
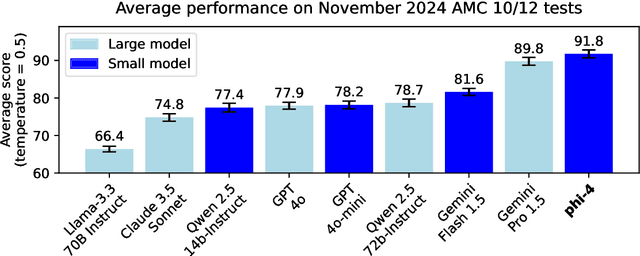
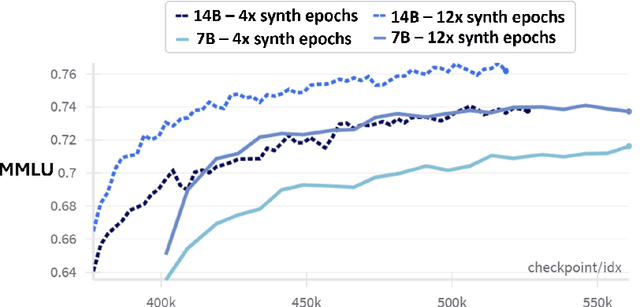
Phi-4 Technical Report

We present phi-4, a 14-billion parameter language model developed with a training recipe that is centrally focused on data quality. Unlike most language models, where pre-training is based primarily on organic data sources such as web content or code, phi-4 strategically incorporates synthetic data throughout the training process. While previous models in the Phi family largely distill the capabilities of a teacher model (specifically GPT-4), phi-4 substantially surpasses its teacher model on STEM-focused QA capabilities, giving evidence that our data-generation and post-training techniques go beyond distillation. Despite minimal changes to the phi-3 architecture, phi-4 achieves strong performance relative to its size -- especially on reasoning-focused benchmarks -- due to improved data, training curriculum, and innovations in the post-training scheme.

Can Models Learn Skill Composition from Examples?

As large language models (LLMs) become increasingly advanced, their ability to exhibit compositional generalization -- the capacity to combine learned skills in novel ways not encountered during training -- has garnered significant attention. This type of generalization, particularly in scenarios beyond training data, is also of great interest in the study of AI safety and alignment. A recent study introduced the SKILL-MIX evaluation, where models are tasked with composing a short paragraph demonstrating the use of a specified $k$-tuple of language skills. While small models struggled with composing even with $k=3$, larger models like GPT-4 performed reasonably well with $k=5$ and $6$. In this paper, we employ a setup akin to SKILL-MIX to evaluate the capacity of smaller models to learn compositional generalization from examples. Utilizing a diverse set of language skills -- including rhetorical, literary, reasoning, theory of mind, and common sense -- GPT-4 was used to generate text samples that exhibit random subsets of $k$ skills. Subsequent fine-tuning of 7B and 13B parameter models on these combined skill texts, for increasing values of $k$, revealed the following findings: (1) Training on combinations of $k=2$ and $3$ skills results in noticeable improvements in the ability to compose texts with $k=4$ and $5$ skills, despite models never having seen such examples during training. (2) When skill categories are split into training and held-out groups, models significantly improve at composing texts with held-out skills during testing despite having only seen training skills during fine-tuning, illustrating the efficacy of the training approach even with previously unseen skills. This study also suggests that incorporating skill-rich (potentially synthetic) text into training can substantially enhance the compositional capabilities of models.

ConceptMix: A Compositional Image Generation Benchmark with Controllable Difficulty

Compositionality is a critical capability in Text-to-Image (T2I) models, as it reflects their ability to understand and combine multiple concepts from text descriptions. Existing evaluations of compositional capability rely heavily on human-designed text prompts or fixed templates, limiting their diversity and complexity, and yielding low discriminative power. We propose ConceptMix, a scalable, controllable, and customizable benchmark which automatically evaluates compositional generation ability of T2I models. This is done in two stages. First, ConceptMix generates the text prompts: concretely, using categories of visual concepts (e.g., objects, colors, shapes, spatial relationships), it randomly samples an object and k-tuples of visual concepts, then uses GPT4-o to generate text prompts for image generation based on these sampled concepts. Second, ConceptMix evaluates the images generated in response to these prompts: concretely, it checks how many of the k concepts actually appeared in the image by generating one question per visual concept and using a strong VLM to answer them. Through administering ConceptMix to a diverse set of T2I models (proprietary as well as open ones) using increasing values of k, we show that our ConceptMix has higher discrimination power than earlier benchmarks. Specifically, ConceptMix reveals that the performance of several models, especially open models, drops dramatically with increased k. Importantly, it also provides insight into the lack of prompt diversity in widely-used training datasets. Additionally, we conduct extensive human studies to validate the design of ConceptMix and compare our automatic grading with human judgement. We hope it will guide future T2I model development.

AI-Assisted Generation of Difficult Math Questions

Current LLM training positions mathematical reasoning as a core capability. With publicly available sources fully tapped, there is unmet demand for diverse and challenging math questions. Relying solely on human experts is both time-consuming and costly, while LLM-generated questions often lack the requisite diversity and difficulty. We present a design framework that combines the strengths of LLMs with a human-in-the-loop approach to generate a diverse array of challenging math questions. We leverage LLM metacognition skills [Didolkar et al., 2024] of a strong LLM to extract core "skills" from existing math datasets. These skills serve as the basis for generating novel and difficult questions by prompting the LLM with random pairs of core skills. The use of two different skills within each question makes finding such questions an "out of distribution" task for both LLMs and humans. Our pipeline employs LLMs to iteratively generate and refine questions and solutions through multiturn prompting. Human annotators then verify and further refine the questions, with their efficiency enhanced via further LLM interactions. Applying this pipeline on skills extracted from the MATH dataset [Hendrycks et al., 2021] resulted in MATH$^2$ - a dataset of higher-quality math questions, as evidenced by: (a) Lower performance of all models on MATH$^2$ than on MATH (b) Higher performance on MATH when using MATH$^2$ questions as in-context examples. Although focused on mathematics, our methodology seems applicable to other domains requiring structured reasoning, and potentially as a component of scalable oversight. Also of interest is a striking relationship observed between models' performance on the new dataset: the success rate on MATH$^2$ is the square on MATH, suggesting that successfully solving the question in MATH$^2$ requires a nontrivial combination of two distinct math skills.

Keeping LLMs Aligned After Fine-tuning: The Crucial Role of Prompt Templates

Public LLMs such as the Llama 2-Chat have driven huge activity in LLM research. These models underwent alignment training and were considered safe. Recently Qi et al. (2023) reported that even benign fine-tuning (e.g., on seemingly safe datasets) can give rise to unsafe behaviors in the models. The current paper is about methods and best practices to mitigate such loss of alignment. Through extensive experiments on several chat models (Meta's Llama 2-Chat, Mistral AI's Mistral 7B Instruct v0.2, and OpenAI's GPT-3.5 Turbo), this paper uncovers that the prompt templates used during fine-tuning and inference play a crucial role in preserving safety alignment, and proposes the "Pure Tuning, Safe Testing" (PTST) principle -- fine-tune models without a safety prompt, but include it at test time. Fine-tuning experiments on GSM8K, ChatDoctor, and OpenOrca show that PTST significantly reduces the rise of unsafe behaviors, and even almost eliminates them in some cases.

Skill-Mix: a Flexible and Expandable Family of Evaluations for AI models

With LLMs shifting their role from statistical modeling of language to serving as general-purpose AI agents, how should LLM evaluations change? Arguably, a key ability of an AI agent is to flexibly combine, as needed, the basic skills it has learned. The capability to combine skills plays an important role in (human) pedagogy and also in a paper on emergence phenomena (Arora & Goyal, 2023). This work introduces Skill-Mix, a new evaluation to measure ability to combine skills. Using a list of $N$ skills the evaluator repeatedly picks random subsets of $k$ skills and asks the LLM to produce text combining that subset of skills. Since the number of subsets grows like $N^k$, for even modest $k$ this evaluation will, with high probability, require the LLM to produce text significantly different from any text in the training set. The paper develops a methodology for (a) designing and administering such an evaluation, and (b) automatic grading (plus spot-checking by humans) of the results using GPT-4 as well as the open LLaMA-2 70B model. Administering a version of to popular chatbots gave results that, while generally in line with prior expectations, contained surprises. Sizeable differences exist among model capabilities that are not captured by their ranking on popular LLM leaderboards ("cramming for the leaderboard"). Furthermore, simple probability calculations indicate that GPT-4's reasonable performance on $k=5$ is suggestive of going beyond "stochastic parrot" behavior (Bender et al., 2021), i.e., it combines skills in ways that it had not seen during training. We sketch how the methodology can lead to a Skill-Mix based eco-system of open evaluations for AI capabilities of future models.

Tensor Programs VI: Feature Learning in Infinite-Depth Neural Networks

By classifying infinite-width neural networks and identifying the *optimal* limit, Tensor Programs IV and V demonstrated a universal way, called $\mu$P, for *widthwise hyperparameter transfer*, i.e., predicting optimal hyperparameters of wide neural networks from narrow ones. Here we investigate the analogous classification for *depthwise parametrizations* of deep residual networks (resnets). We classify depthwise parametrizations of block multiplier and learning rate by their infinite-width-then-depth limits. In resnets where each block has only one layer, we identify a unique optimal parametrization, called Depth-$\mu$P that extends $\mu$P and show empirically it admits depthwise hyperparameter transfer. We identify *feature diversity* as a crucial factor in deep networks, and Depth-$\mu$P can be characterized as maximizing both feature learning and feature diversity. Exploiting this, we find that absolute value, among all homogeneous nonlinearities, maximizes feature diversity and indeed empirically leads to significantly better performance. However, if each block is deeper (such as modern transformers), then we find fundamental limitations in all possible infinite-depth limits of such parametrizations, which we illustrate both theoretically and empirically on simple networks as well as Megatron transformer trained on Common Crawl.

New Definitions and Evaluations for Saliency Methods: Staying Intrinsic, Complete and Sound

Saliency methods compute heat maps that highlight portions of an input that were most {\em important} for the label assigned to it by a deep net. Evaluations of saliency methods convert this heat map into a new {\em masked input} by retaining the $k$ highest-ranked pixels of the original input and replacing the rest with \textquotedblleft uninformative\textquotedblright\ pixels, and checking if the net's output is mostly unchanged. This is usually seen as an {\em explanation} of the output, but the current paper highlights reasons why this inference of causality may be suspect. Inspired by logic concepts of {\em completeness \& soundness}, it observes that the above type of evaluation focuses on completeness of the explanation, but ignores soundness. New evaluation metrics are introduced to capture both notions, while staying in an {\em intrinsic} framework -- i.e., using the dataset and the net, but no separately trained nets, human evaluations, etc. A simple saliency method is described that matches or outperforms prior methods in the evaluations. Experiments also suggest new intrinsic justifications, based on soundness, for popular heuristic tricks such as TV regularization and upsampling.

A Kernel-Based View of Language Model Fine-Tuning

It has become standard to solve NLP tasks by fine-tuning pre-trained language models (LMs), especially in low-data settings. There is minimal theoretical understanding of empirical success, e.g., why fine-tuning a model with $10^8$ or more parameters on a couple dozen training points does not result in overfitting. We investigate whether the Neural Tangent Kernel (NTK) - which originated as a model to study the gradient descent dynamics of infinitely wide networks with suitable random initialization - describes fine-tuning of pre-trained LMs. This study was inspired by the decent performance of NTK for computer vision tasks (Wei et al., 2022). We also extend the NTK formalism to fine-tuning with Adam. We present extensive experiments that show that once the downstream task is formulated as a language modeling problem through prompting, the NTK lens can often reasonably describe the model updates during fine-tuning with both SGD and Adam. This kernel view also suggests an explanation for success of parameter-efficient subspace-based fine-tuning methods. Finally, we suggest a path toward a formal explanation for our findings via Tensor Programs (Yang, 2020).

Enhanced Convolutional Neural Tangent Kernels

Recent research shows that for training with $\ell_2$ loss, convolutional neural networks (CNNs) whose width (number of channels in convolutional layers) goes to infinity correspond to regression with respect to the CNN Gaussian Process kernel (CNN-GP) if only the last layer is trained, and correspond to regression with respect to the Convolutional Neural Tangent Kernel (CNTK) if all layers are trained. An exact algorithm to compute CNTK (Arora et al., 2019) yielded the finding that classification accuracy of CNTK on CIFAR-10 is within 6-7% of that of that of the corresponding CNN architecture (best figure being around 78%) which is interesting performance for a fixed kernel. Here we show how to significantly enhance the performance of these kernels using two ideas. (1) Modifying the kernel using a new operation called Local Average Pooling (LAP) which preserves efficient computability of the kernel and inherits the spirit of standard data augmentation using pixel shifts. Earlier papers were unable to incorporate naive data augmentation because of the quadratic training cost of kernel regression. This idea is inspired by Global Average Pooling (GAP), which we show for CNN-GP and CNTK is equivalent to full translation data augmentation. (2) Representing the input image using a pre-processing technique proposed by Coates et al. (2011), which uses a single convolutional layer composed of random image patches. On CIFAR-10, the resulting kernel, CNN-GP with LAP and horizontal flip data augmentation, achieves 89% accuracy, matching the performance of AlexNet (Krizhevsky et al., 2012). Note that this is the best such result we know of for a classifier that is not a trained neural network. Similar improvements are obtained for Fashion-MNIST.