Learning Compositional Functions with Transformers from Easy-to-Hard Data

Transformer-based language models have demonstrated impressive capabilities across a range of complex reasoning tasks. Prior theoretical work exploring the expressive power of transformers has shown that they can efficiently perform multi-step reasoning tasks involving parallelizable computations. However, the learnability of such constructions, particularly the conditions on the data distribution that enable efficient learning via gradient-based optimization, remains an open question. Towards answering this question, in this work we study the learnability of the $k$-fold composition task, which requires computing an interleaved composition of $k$ input permutations and $k$ hidden permutations, and can be expressed by a transformer with $O(\log k)$ layers. On the negative front, we prove a Statistical Query (SQ) lower bound showing that any SQ learner that makes only polynomially-many queries to an SQ oracle for the $k$-fold composition task distribution must have sample size exponential in $k$, thus establishing a statistical-computational gap. On the other hand, we show that this function class can be efficiently learned, with runtime and sample complexity polynomial in $k$, by gradient descent on an $O(\log k)$-depth transformer via two different curriculum learning strategies: one in which data consists of $k'$-fold composition functions with $k' \le k$ presented in increasing difficulty, and another in which all such data is presented simultaneously. Our work sheds light on the necessity and sufficiency of having both easy and hard examples in the data distribution for transformers to learn complex compositional tasks.

Emergence and scaling laws in SGD learning of shallow neural networks

We study the complexity of online stochastic gradient descent (SGD) for learning a two-layer neural network with $P$ neurons on isotropic Gaussian data: $f_*(\boldsymbol{x}) = \sum_{p=1}^P a_p\cdot \sigma(\langle\boldsymbol{x},\boldsymbol{v}_p^*\rangle)$, $\boldsymbol{x} \sim \mathcal{N}(0,\boldsymbol{I}_d)$, where the activation $\sigma:\mathbb{R}\to\mathbb{R}$ is an even function with information exponent $k_*>2$ (defined as the lowest degree in the Hermite expansion), $\{\boldsymbol{v}^*_p\}_{p\in[P]}\subset \mathbb{R}^d$ are orthonormal signal directions, and the non-negative second-layer coefficients satisfy $\sum_{p} a_p^2=1$. We focus on the challenging ``extensive-width'' regime $P\gg 1$ and permit diverging condition number in the second-layer, covering as a special case the power-law scaling $a_p\asymp p^{-\beta}$ where $\beta\in\mathbb{R}_{\ge 0}$. We provide a precise analysis of SGD dynamics for the training of a student two-layer network to minimize the mean squared error (MSE) objective, and explicitly identify sharp transition times to recover each signal direction. In the power-law setting, we characterize scaling law exponents for the MSE loss with respect to the number of training samples and SGD steps, as well as the number of parameters in the student neural network. Our analysis entails that while the learning of individual teacher neurons exhibits abrupt transitions, the juxtaposition of $P\gg 1$ emergent learning curves at different timescales leads to a smooth scaling law in the cumulative objective.

Propagation of Chaos in One-hidden-layer Neural Networks beyond Logarithmic Time

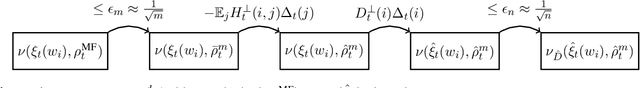
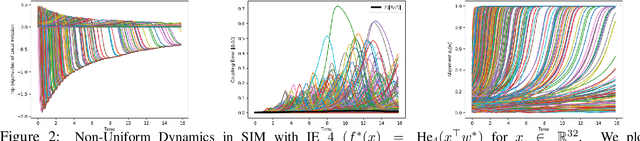
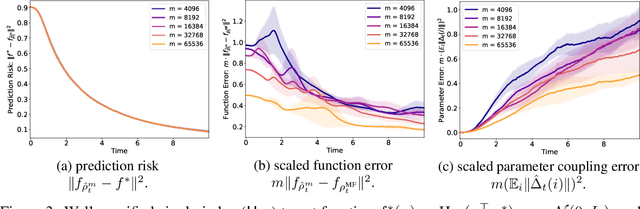
We study the approximation gap between the dynamics of a polynomial-width neural network and its infinite-width counterpart, both trained using projected gradient descent in the mean-field scaling regime. We demonstrate how to tightly bound this approximation gap through a differential equation governed by the mean-field dynamics. A key factor influencing the growth of this ODE is the local Hessian of each particle, defined as the derivative of the particle's velocity in the mean-field dynamics with respect to its position. We apply our results to the canonical feature learning problem of estimating a well-specified single-index model; we permit the information exponent to be arbitrarily large, leading to convergence times that grow polynomially in the ambient dimension $d$. We show that, due to a certain ``self-concordance'' property in these problems -- where the local Hessian of a particle is bounded by a constant times the particle's velocity -- polynomially many neurons are sufficient to closely approximate the mean-field dynamics throughout training.

When Do Transformers Outperform Feedforward and Recurrent Networks? A Statistical Perspective

Theoretical efforts to prove advantages of Transformers in comparison with classical architectures such as feedforward and recurrent neural networks have mostly focused on representational power. In this work, we take an alternative perspective and prove that even with infinite compute, feedforward and recurrent networks may suffer from larger sample complexity compared to Transformers, as the latter can adapt to a form of dynamic sparsity. Specifically, we consider a sequence-to-sequence data generating model on sequences of length $N$, in which the output at each position depends only on $q$ relevant tokens with $q \ll N$, and the positions of these tokens are described in the input prompt. We prove that a single-layer Transformer can learn this model if and only if its number of attention heads is at least $q$, in which case it achieves a sample complexity almost independent of $N$, while recurrent networks require $N^{\Omega(1)}$ samples on the same problem. If we simplify this model, recurrent networks may achieve a complexity almost independent of $N$, while feedforward networks still require $N$ samples. Consequently, our proposed sparse retrieval model illustrates a natural hierarchy in sample complexity across these architectures.

Metastable Dynamics of Chain-of-Thought Reasoning: Provable Benefits of Search, RL and Distillation

A key paradigm to improve the reasoning capabilities of large language models (LLMs) is to allocate more inference-time compute to search against a verifier or reward model. This process can then be utilized to refine the pretrained model or distill its reasoning patterns into more efficient models. In this paper, we study inference-time compute by viewing chain-of-thought (CoT) generation as a metastable Markov process: easy reasoning steps (e.g., algebraic manipulations) form densely connected clusters, while hard reasoning steps (e.g., applying a relevant theorem) create sparse, low-probability edges between clusters, leading to phase transitions at longer timescales. Under this framework, we prove that implementing a search protocol that rewards sparse edges improves CoT by decreasing the expected number of steps to reach different clusters. In contrast, we establish a limit on reasoning capability when the model is restricted to local information of the pretrained graph. We also show that the information gained by search can be utilized to obtain a better reasoning model: (1) the pretrained model can be directly finetuned to favor sparse edges via policy gradient methods, and moreover (2) a compressed metastable representation of the reasoning dynamics can be distilled into a smaller, more efficient model.

Pretrained transformer efficiently learns low-dimensional target functions in-context

Transformers can efficiently learn in-context from example demonstrations. Most existing theoretical analyses studied the in-context learning (ICL) ability of transformers for linear function classes, where it is typically shown that the minimizer of the pretraining loss implements one gradient descent step on the least squares objective. However, this simplified linear setting arguably does not demonstrate the statistical efficiency of ICL, since the pretrained transformer does not outperform directly solving linear regression on the test prompt. In this paper, we study ICL of a nonlinear function class via transformer with nonlinear MLP layer: given a class of \textit{single-index} target functions $f_*(\boldsymbol{x}) = \sigma_*(\langle\boldsymbol{x},\boldsymbol{\beta}\rangle)$, where the index features $\boldsymbol{\beta}\in\mathbb{R}^d$ are drawn from a $r$-dimensional subspace, we show that a nonlinear transformer optimized by gradient descent (with a pretraining sample complexity that depends on the \textit{information exponent} of the link functions $\sigma_*$) learns $f_*$ in-context with a prompt length that only depends on the dimension of the distribution of target functions $r$; in contrast, any algorithm that directly learns $f_*$ on test prompt yields a statistical complexity that scales with the ambient dimension $d$. Our result highlights the adaptivity of the pretrained transformer to low-dimensional structures of the function class, which enables sample-efficient ICL that outperforms estimators that only have access to the in-context data.

Learning Multi-Index Models with Neural Networks via Mean-Field Langevin Dynamics

We study the problem of learning multi-index models in high-dimensions using a two-layer neural network trained with the mean-field Langevin algorithm. Under mild distributional assumptions on the data, we characterize the effective dimension $d_{\mathrm{eff}}$ that controls both sample and computational complexity by utilizing the adaptivity of neural networks to latent low-dimensional structures. When the data exhibit such a structure, $d_{\mathrm{eff}}$ can be significantly smaller than the ambient dimension. We prove that the sample complexity grows almost linearly with $d_{\mathrm{eff}}$, bypassing the limitations of the information and generative exponents that appeared in recent analyses of gradient-based feature learning. On the other hand, the computational complexity may inevitably grow exponentially with $d_{\mathrm{eff}}$ in the worst-case scenario. Motivated by improving computational complexity, we take the first steps towards polynomial time convergence of the mean-field Langevin algorithm by investigating a setting where the weights are constrained to be on a compact manifold with positive Ricci curvature, such as the hypersphere. There, we study assumptions under which polynomial time convergence is achievable, whereas similar assumptions in the Euclidean setting lead to exponential time complexity.

Learning sum of diverse features: computational hardness and efficient gradient-based training for ridge combinations

We study the computational and sample complexity of learning a target function $f_*:\mathbb{R}^d\to\mathbb{R}$ with additive structure, that is, $f_*(x) = \frac{1}{\sqrt{M}}\sum_{m=1}^M f_m(\langle x, v_m\rangle)$, where $f_1,f_2,...,f_M:\mathbb{R}\to\mathbb{R}$ are nonlinear link functions of single-index models (ridge functions) with diverse and near-orthogonal index features $\{v_m\}_{m=1}^M$, and the number of additive tasks $M$ grows with the dimensionality $M\asymp d^\gamma$ for $\gamma\ge 0$. This problem setting is motivated by the classical additive model literature, the recent representation learning theory of two-layer neural network, and large-scale pretraining where the model simultaneously acquires a large number of "skills" that are often localized in distinct parts of the trained network. We prove that a large subset of polynomial $f_*$ can be efficiently learned by gradient descent training of a two-layer neural network, with a polynomial statistical and computational complexity that depends on the number of tasks $M$ and the information exponent of $f_m$, despite the unknown link function and $M$ growing with the dimensionality. We complement this learnability guarantee with computational hardness result by establishing statistical query (SQ) lower bounds for both the correlational SQ and full SQ algorithms.

Neural network learns low-dimensional polynomials with SGD near the information-theoretic limit

We study the problem of gradient descent learning of a single-index target function $f_*(\boldsymbol{x}) = \textstyle\sigma_*\left(\langle\boldsymbol{x},\boldsymbol{\theta}\rangle\right)$ under isotropic Gaussian data in $\mathbb{R}^d$, where the link function $\sigma_*:\mathbb{R}\to\mathbb{R}$ is an unknown degree $q$ polynomial with information exponent $p$ (defined as the lowest degree in the Hermite expansion). Prior works showed that gradient-based training of neural networks can learn this target with $n\gtrsim d^{\Theta(p)}$ samples, and such statistical complexity is predicted to be necessary by the correlational statistical query lower bound. Surprisingly, we prove that a two-layer neural network optimized by an SGD-based algorithm learns $f_*$ of arbitrary polynomial link function with a sample and runtime complexity of $n \asymp T \asymp C(q) \cdot d\mathrm{polylog} d$, where constant $C(q)$ only depends on the degree of $\sigma_*$, regardless of information exponent; this dimension dependence matches the information theoretic limit up to polylogarithmic factors. Core to our analysis is the reuse of minibatch in the gradient computation, which gives rise to higher-order information beyond correlational queries.

Nonlinear spiked covariance matrices and signal propagation in deep neural networks

Many recent works have studied the eigenvalue spectrum of the Conjugate Kernel (CK) defined by the nonlinear feature map of a feedforward neural network. However, existing results only establish weak convergence of the empirical eigenvalue distribution, and fall short of providing precise quantitative characterizations of the ''spike'' eigenvalues and eigenvectors that often capture the low-dimensional signal structure of the learning problem. In this work, we characterize these signal eigenvalues and eigenvectors for a nonlinear version of the spiked covariance model, including the CK as a special case. Using this general result, we give a quantitative description of how spiked eigenstructure in the input data propagates through the hidden layers of a neural network with random weights. As a second application, we study a simple regime of representation learning where the weight matrix develops a rank-one signal component over training and characterize the alignment of the target function with the spike eigenvector of the CK on test data.