A System-Level View on Out-of-Distribution Data in Robotics

When testing conditions differ from those represented in training data, so-called out-of-distribution (OOD) inputs can mar the reliability of black-box learned components in the modern robot autonomy stack. Therefore, coping with OOD data is an important challenge on the path towards trustworthy learning-enabled open-world autonomy. In this paper, we aim to demystify the topic of OOD data and its associated challenges in the context of data-driven robotic systems, drawing connections to emerging paradigms in the ML community that study the effect of OOD data on learned models in isolation. We argue that as roboticists, we should reason about the overall system-level competence of a robot as it performs tasks in OOD conditions. We highlight key research questions around this system-level view of OOD problems to guide future research toward safe and reliable learning-enabled autonomy.

Online Distribution Shift Detection via Recency Prediction

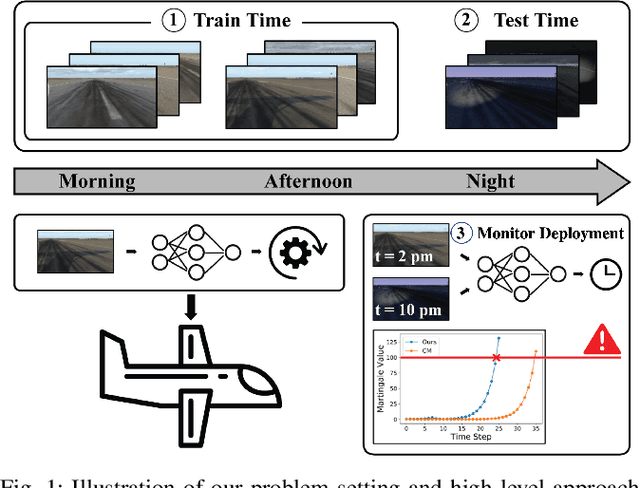
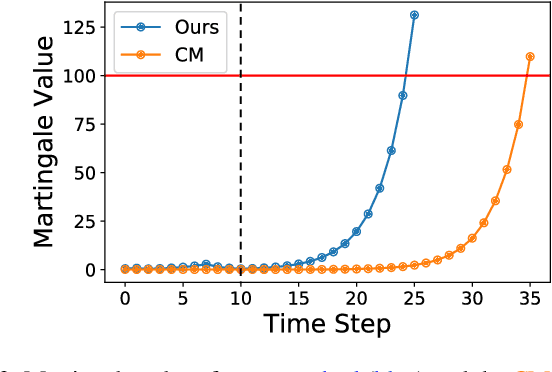
When deploying modern machine learning-enabled robotic systems in high-stakes applications, detecting distribution shift is critical. However, most existing methods for detecting distribution shift are not well-suited to robotics settings, where data often arrives in a streaming fashion and may be very high-dimensional. In this work, we present an online method for detecting distribution shift with guarantees on the false positive rate - i.e., when there is no distribution shift, our system is very unlikely (with probability $< \epsilon$) to falsely issue an alert; any alerts that are issued should therefore be heeded. Our method is specifically designed for efficient detection even with high dimensional data, and it empirically achieves up to 11x faster detection on realistic robotics settings compared to prior work while maintaining a low false negative rate in practice (whenever there is a distribution shift in our experiments, our method indeed emits an alert).

Learning Autonomous Vehicle Safety Concepts from Demonstrations

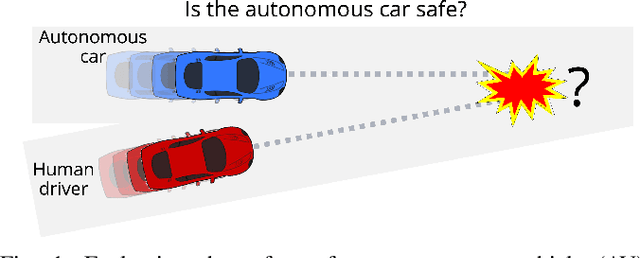
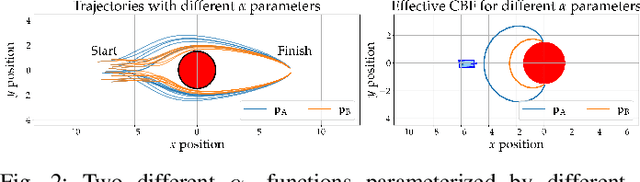
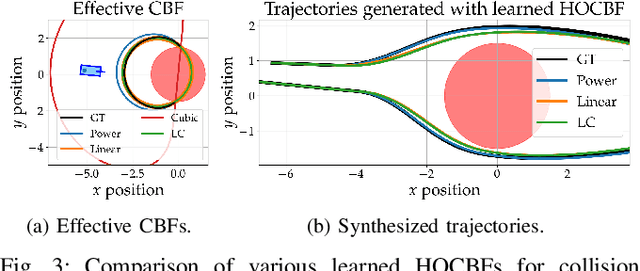
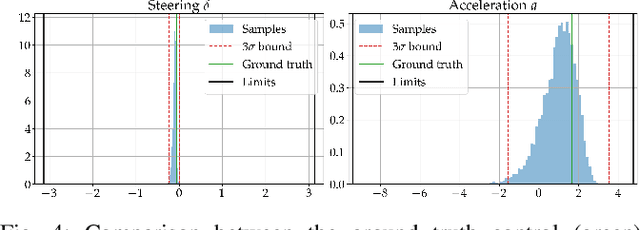
Evaluating the safety of an autonomous vehicle (AV) depends on the behavior of surrounding agents which can be heavily influenced by factors such as environmental context and informally-defined driving etiquette. A key challenge is in determining a minimum set of assumptions on what constitutes reasonable foreseeable behaviors of other road users for the development of AV safety models and techniques. In this paper, we propose a data-driven AV safety design methodology that first learns ``reasonable'' behavioral assumptions from data, and then synthesizes an AV safety concept using these learned behavioral assumptions. We borrow techniques from control theory, namely high order control barrier functions and Hamilton-Jacobi reachability, to provide inductive bias to aid interpretability, verifiability, and tractability of our approach. In our experiments, we learn an AV safety concept using demonstrations collected from a highway traffic-weaving scenario, compare our learned concept to existing baselines, and showcase its efficacy in evaluating real-world driving logs.

Data Lifecycle Management in Evolving Input Distributions for Learning-based Aerospace Applications

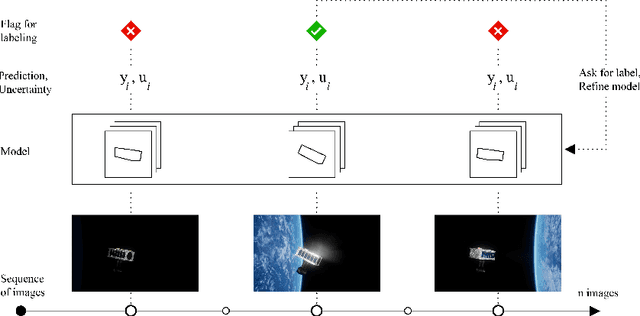
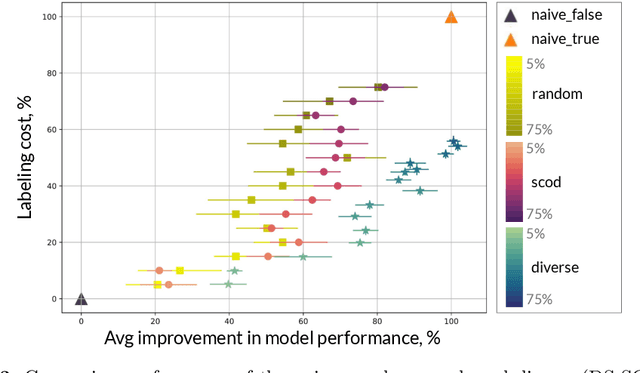
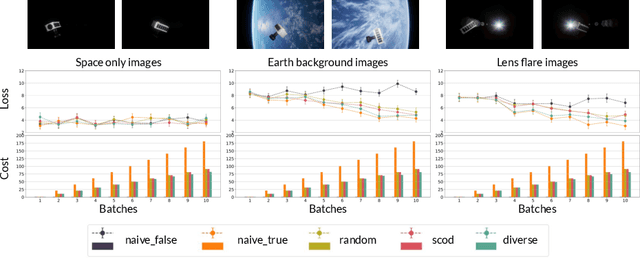
As input distributions evolve over a mission lifetime, maintaining performance of learning-based models becomes challenging. This paper presents a framework to incrementally retrain a model by selecting a subset of test inputs to label, which allows the model to adapt to changing input distributions. Algorithms within this framework are evaluated based on (1) model performance throughout mission lifetime and (2) cumulative costs associated with labeling and model retraining. We provide an open-source benchmark of a satellite pose estimation model trained on images of a satellite in space and deployed in novel scenarios (e.g., different backgrounds or misbehaving pixels), where algorithms are evaluated on their ability to maintain high performance by retraining on a subset of inputs. We also propose a novel algorithm to select a diverse subset of inputs for labeling, by characterizing the information gain from an input using Bayesian uncertainty quantification and choosing a subset that maximizes collective information gain using concepts from batch active learning. We show that our algorithm outperforms others on the benchmark, e.g., achieves comparable performance to an algorithm that labels 100% of inputs, while only labeling 50% of inputs, resulting in low costs and high performance over the mission lifetime.

Motion Planning for a Climbing Robot with Stochastic Grasps

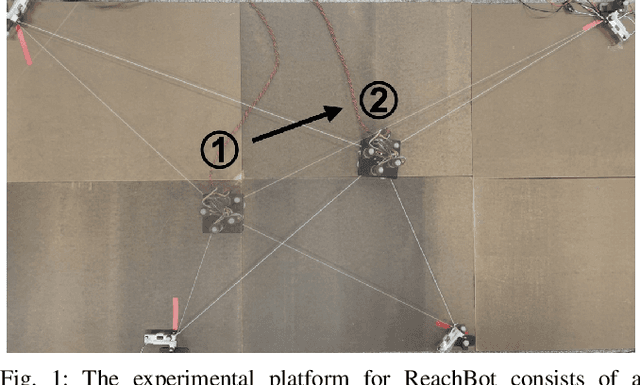
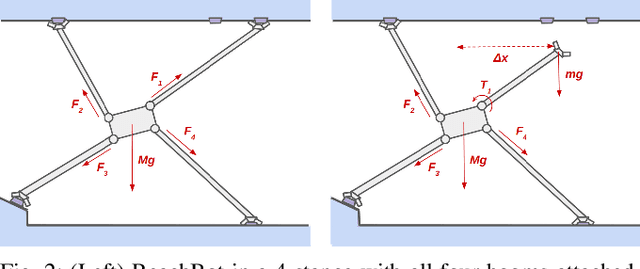
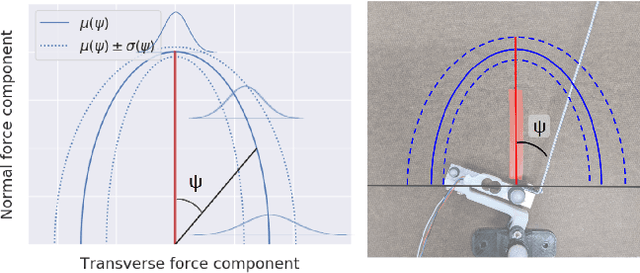
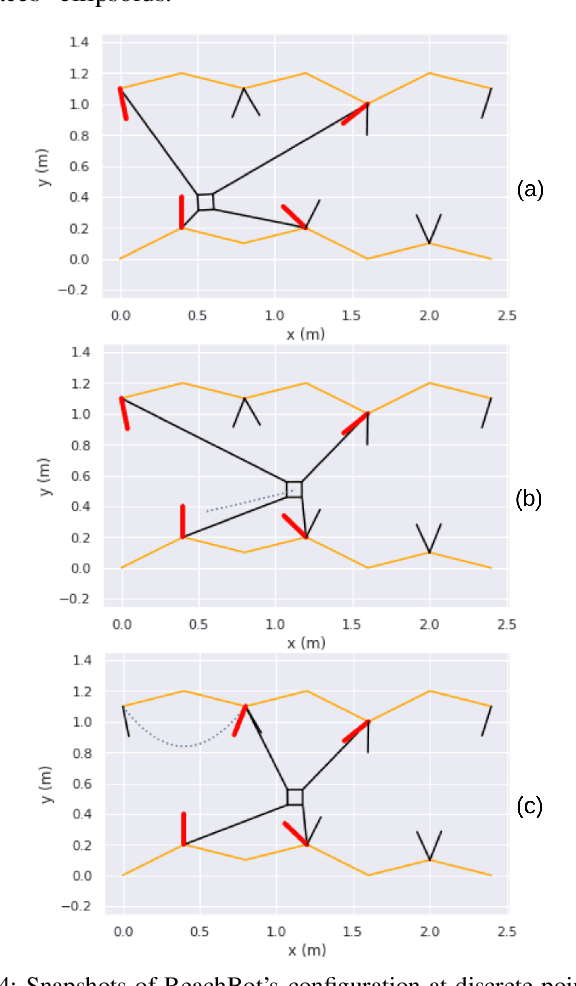
Motion planning for a multi-limbed climbing robot must consider the robot's posture, joint torques, and how it uses contact forces to interact with its environment. This paper focuses on motion planning for a robot that uses nontraditional locomotion to explore unpredictable environments such as martian caves. Our robotic concept, ReachBot, uses extendable and retractable booms as limbs to achieve a large reachable workspace while climbing. Each extendable boom is capped by a microspine gripper designed for grasping rocky surfaces. ReachBot leverages its large workspace to navigate around obstacles, over crevasses, and through challenging terrain. Our planning approach must be versatile to accommodate variable terrain features and robust to mitigate risks from the stochastic nature of grasping with spines. In this paper, we introduce a graph traversal algorithm to select a discrete sequence of grasps based on available terrain features suitable for grasping. This discrete plan is complemented by a decoupled motion planner that considers the alternating phases of body movement and end-effector movement, using a combination of sampling-based planning and sequential convex programming to optimize individual phases. We use our motion planner to plan a trajectory across a simulated 2D cave environment with at least 95% probability of success and demonstrate improved robustness over a baseline trajectory. Finally, we verify our motion planning algorithm through experimentation on a 2D planar prototype.

Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots

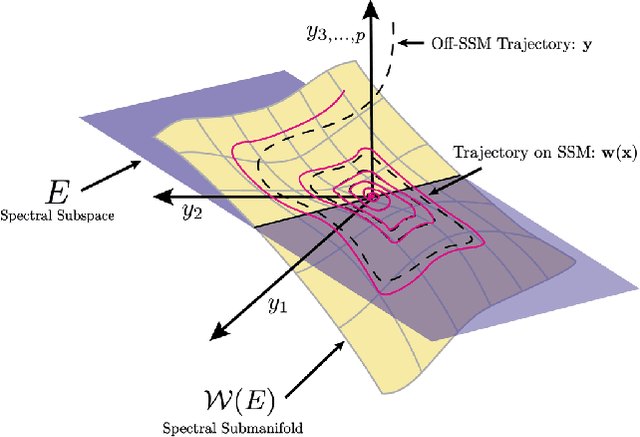
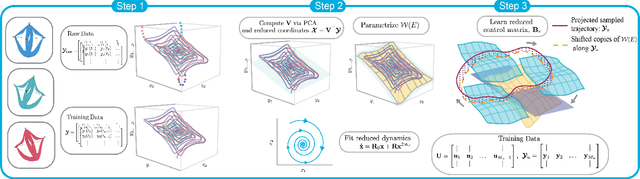
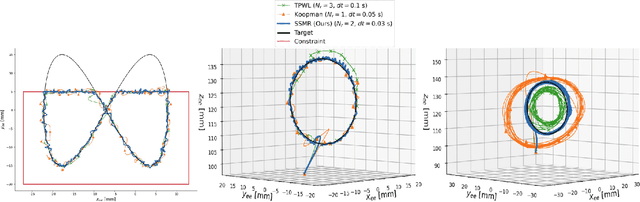
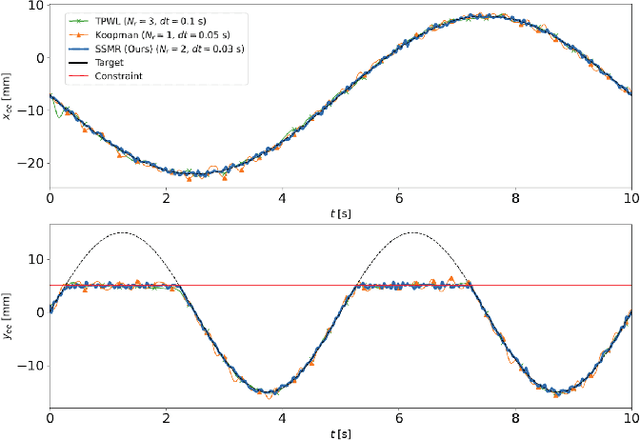
Modeling and control of high-dimensional, nonlinear robotic systems remains a challenging task. While various model- and learning-based approaches have been proposed to address these challenges, they broadly lack generalizability to different control tasks and rarely preserve the structure of the dynamics. In this work, we propose a new, data-driven approach for extracting low-dimensional models from data using Spectral Submanifold Reduction (SSMR). In contrast to other data-driven methods which fit dynamical models to training trajectories, we identify the dynamics on generic, low-dimensional attractors embedded in the full phase space of the robotic system. This allows us to obtain computationally-tractable models for control which preserve the system's dominant dynamics and better track trajectories radically different from the training data. We demonstrate the superior performance and generalizability of SSMR in dynamic trajectory tracking tasks vis-a-vis the state of the art, including Koopman operator-based approaches.

Using Spectral Submanifolds for Nonlinear Periodic Control

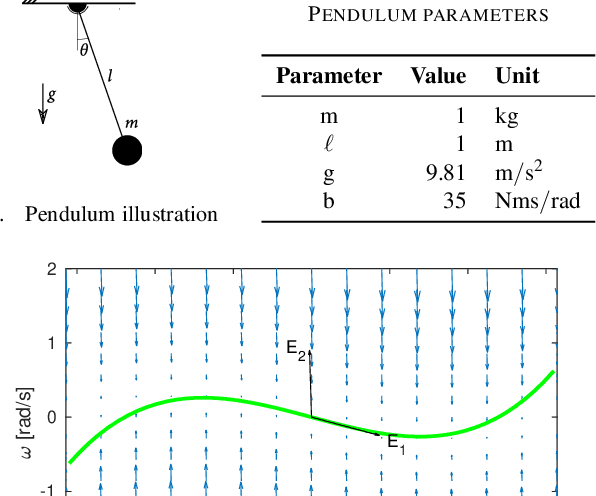
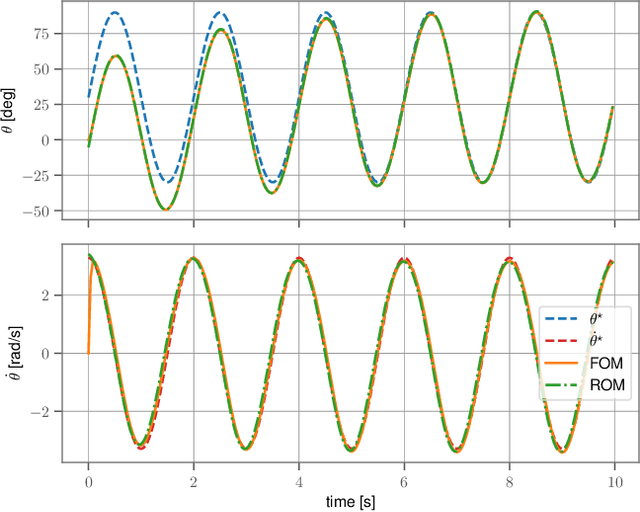
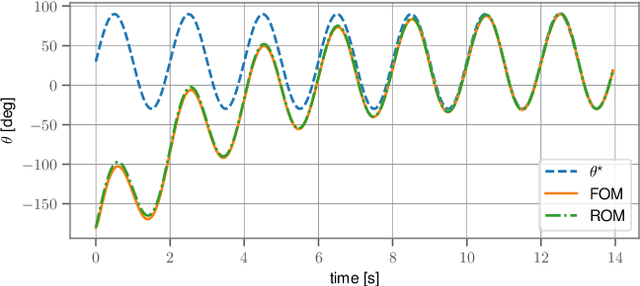
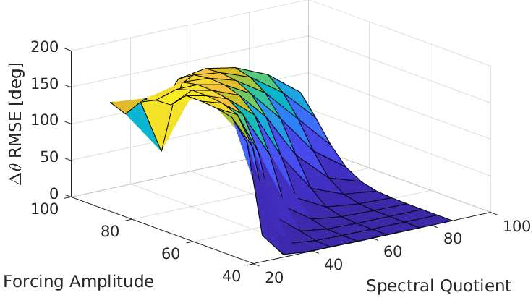
Very high dimensional nonlinear systems arise in many engineering problems due to semi-discretization of the governing partial differential equations, e.g. through finite element methods. The complexity of these systems present computational challenges for direct application to automatic control. While model reduction has seen ubiquitous applications in control, the use of nonlinear model reduction methods in this setting remains difficult. The problem lies in preserving the structure of the nonlinear dynamics in the reduced order model for high-fidelity control. In this work, we leverage recent advances in Spectral Submanifold (SSM) theory to enable model reduction under well-defined assumptions for the purpose of efficiently synthesizing feedback controllers.

Interaction-Dynamics-Aware Perception Zones for Obstacle Detection Safety Evaluation

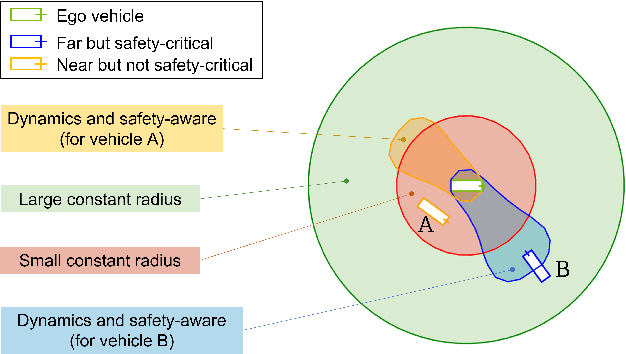
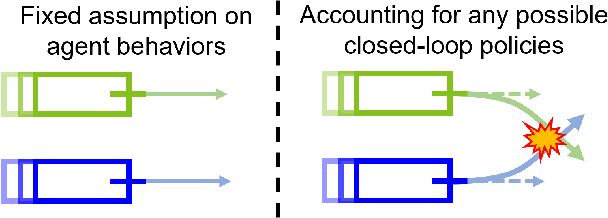
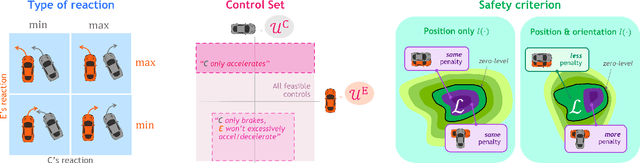
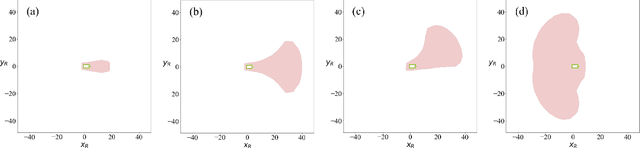
To enable safe autonomous vehicle (AV) operations, it is critical that an AV's obstacle detection module can reliably detect obstacles that pose a safety threat (i.e., are safety-critical). It is therefore desirable that the evaluation metric for the perception system captures the safety-criticality of objects. Unfortunately, existing perception evaluation metrics tend to make strong assumptions about the objects and ignore the dynamic interactions between agents, and thus do not accurately capture the safety risks in reality. To address these shortcomings, we introduce an interaction-dynamics-aware obstacle detection evaluation metric by accounting for closed-loop dynamic interactions between an ego vehicle and obstacles in the scene. By borrowing existing theory from optimal control theory, namely Hamilton-Jacobi reachability, we present a computationally tractable method for constructing a ``safety zone'': a region in state space that defines where safety-critical obstacles lie for the purpose of defining safety metrics. Our proposed safety zone is mathematically complete, and can be easily computed to reflect a variety of safety requirements. Using an off-the-shelf detection algorithm from the nuScenes detection challenge leaderboard, we demonstrate that our approach is computationally lightweight, and can better capture safety-critical perception errors than a baseline approach.

Robust-RRT: Probabilistically-Complete Motion Planning for Uncertain Nonlinear Systems

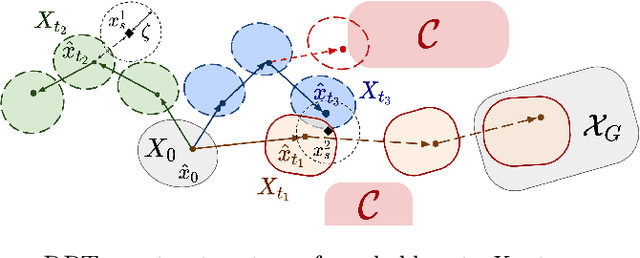
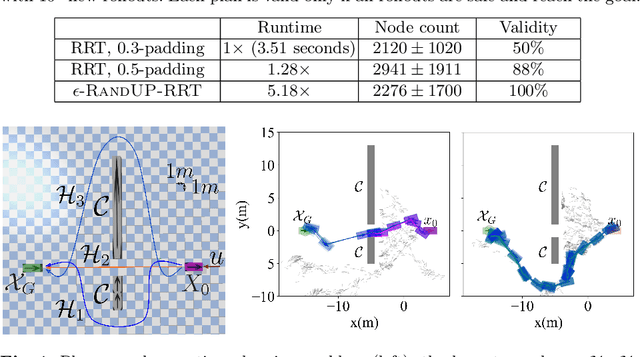
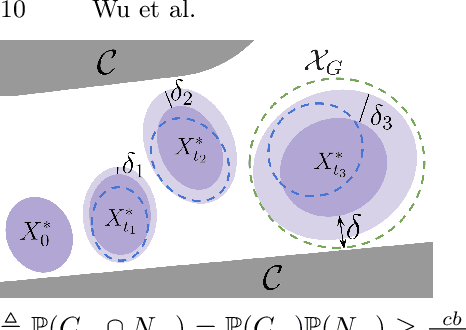
Robust motion planning entails computing a global motion plan that is safe under all possible uncertainty realizations, be it in the system dynamics, the robot's initial position, or with respect to external disturbances. Current approaches for robust motion planning either lack theoretical guarantees, or make restrictive assumptions on the system dynamics and uncertainty distributions. In this paper, we address these limitations by proposing the robust rapidly-exploring random-tree (Robust-RRT) algorithm, which integrates forward reachability analysis directly into sampling-based control trajectory synthesis. We prove that Robust-RRT is probabilistically complete (PC) for nonlinear Lipschitz continuous dynamical systems with bounded uncertainty. In other words, Robust-RRT eventually finds a robust motion plan that is feasible under all possible uncertainty realizations assuming such a plan exists. Our analysis applies even to unstable systems that admit only short-horizon feasible plans; this is because we explicitly consider the time evolution of reachable sets along control trajectories. Thanks to the explicit consideration of time dependency in our analysis, PC applies to unstabilizable systems. To the best of our knowledge, this is the most general PC proof for robust sampling-based motion planning, in terms of the types of uncertainties and dynamical systems it can handle. Considering that an exact computation of reachable sets can be computationally expensive for some dynamical systems, we incorporate sampling-based reachability analysis into Robust-RRT and demonstrate our robust planner on nonlinear, underactuated, and hybrid systems.

Second-Order Sensitivity Analysis for Bilevel Optimization

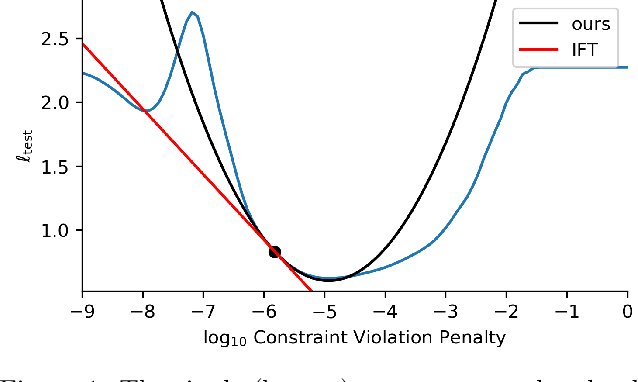
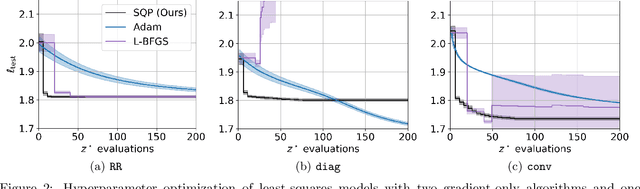
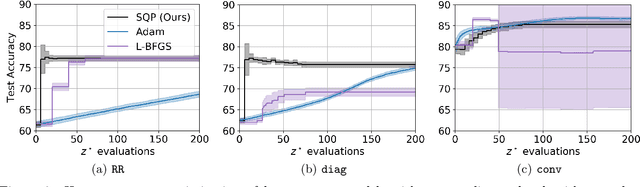
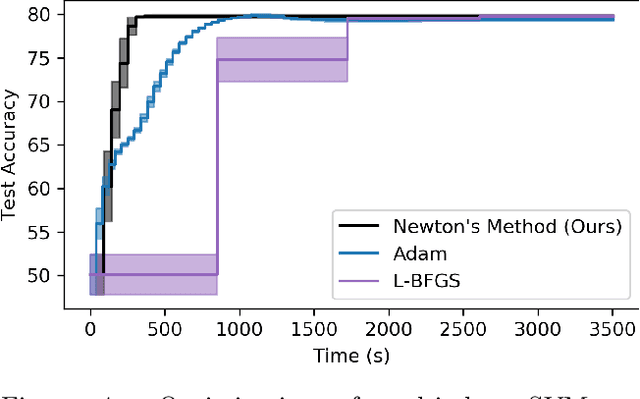
In this work we derive a second-order approach to bilevel optimization, a type of mathematical programming in which the solution to a parameterized optimization problem (the "lower" problem) is itself to be optimized (in the "upper" problem) as a function of the parameters. Many existing approaches to bilevel optimization employ first-order sensitivity analysis, based on the implicit function theorem (IFT), for the lower problem to derive a gradient of the lower problem solution with respect to its parameters; this IFT gradient is then used in a first-order optimization method for the upper problem. This paper extends this sensitivity analysis to provide second-order derivative information of the lower problem (which we call the IFT Hessian), enabling the usage of faster-converging second-order optimization methods at the upper level. Our analysis shows that (i) much of the computation already used to produce the IFT gradient can be reused for the IFT Hessian, (ii) errors bounds derived for the IFT gradient readily apply to the IFT Hessian, (iii) computing IFT Hessians can significantly reduce overall computation by extracting more information from each lower level solve. We corroborate our findings and demonstrate the broad range of applications of our method by applying it to problem instances of least squares hyperparameter auto-tuning, multi-class SVM auto-tuning, and inverse optimal control.