Robust Nonlinear Reduced-Order Model Predictive Control

Real-world systems are often characterized by high-dimensional nonlinear dynamics, making them challenging to control in real time. While reduced-order models (ROMs) are frequently employed in model-based control schemes, dimensionality reduction introduces model uncertainty which can potentially compromise the stability and safety of the original high-dimensional system. In this work, we propose a novel reduced-order model predictive control (ROMPC) scheme to solve constrained optimal control problems for nonlinear, high-dimensional systems. To address the challenges of using ROMs in predictive control schemes, we derive an error bounding system that dynamically accounts for model reduction error. Using these bounds, we design a robust MPC scheme that ensures robust constraint satisfaction, recursive feasibility, and asymptotic stability. We demonstrate the effectiveness of our proposed method in simulations on a high-dimensional soft robot with nearly 10,000 states.

Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots

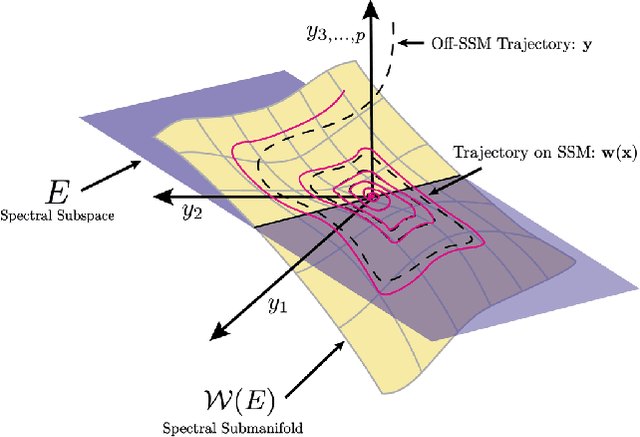
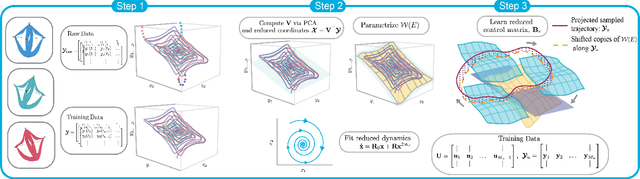
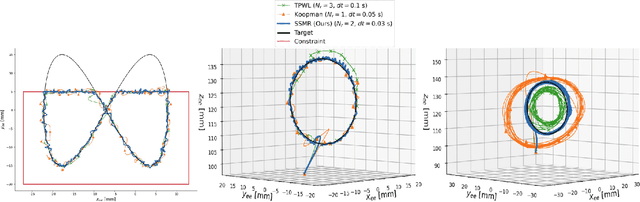
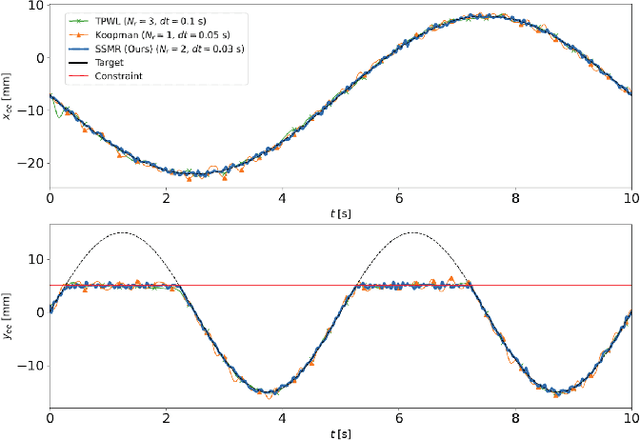
Modeling and control of high-dimensional, nonlinear robotic systems remains a challenging task. While various model- and learning-based approaches have been proposed to address these challenges, they broadly lack generalizability to different control tasks and rarely preserve the structure of the dynamics. In this work, we propose a new, data-driven approach for extracting low-dimensional models from data using Spectral Submanifold Reduction (SSMR). In contrast to other data-driven methods which fit dynamical models to training trajectories, we identify the dynamics on generic, low-dimensional attractors embedded in the full phase space of the robotic system. This allows us to obtain computationally-tractable models for control which preserve the system's dominant dynamics and better track trajectories radically different from the training data. We demonstrate the superior performance and generalizability of SSMR in dynamic trajectory tracking tasks vis-a-vis the state of the art, including Koopman operator-based approaches.

Using Spectral Submanifolds for Nonlinear Periodic Control

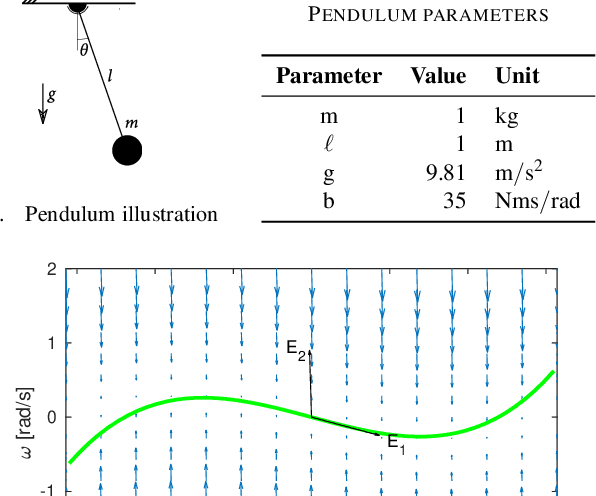
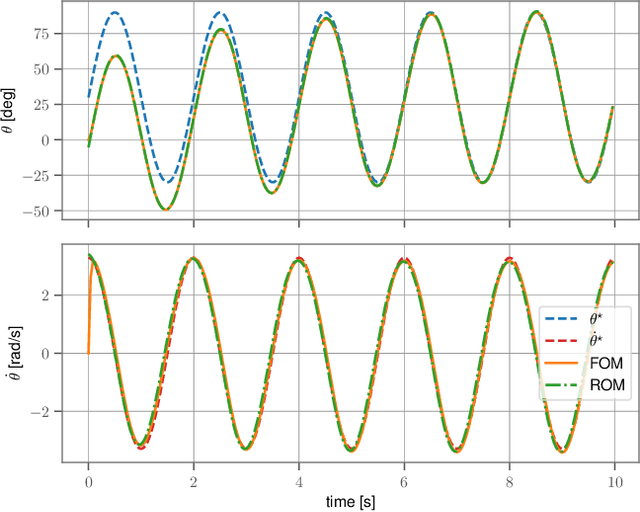
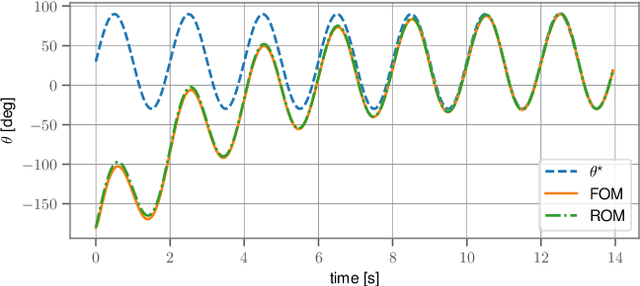
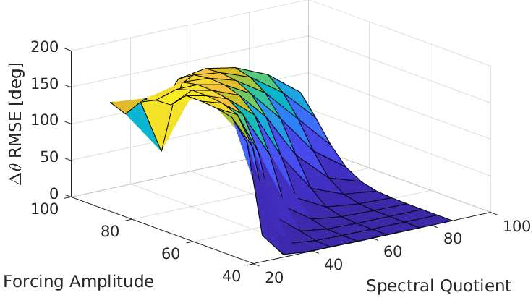
Very high dimensional nonlinear systems arise in many engineering problems due to semi-discretization of the governing partial differential equations, e.g. through finite element methods. The complexity of these systems present computational challenges for direct application to automatic control. While model reduction has seen ubiquitous applications in control, the use of nonlinear model reduction methods in this setting remains difficult. The problem lies in preserving the structure of the nonlinear dynamics in the reduced order model for high-fidelity control. In this work, we leverage recent advances in Spectral Submanifold (SSM) theory to enable model reduction under well-defined assumptions for the purpose of efficiently synthesizing feedback controllers.