Kimi K2: Open Agentic Intelligence

We introduce Kimi K2, a Mixture-of-Experts (MoE) large language model with 32 billion activated parameters and 1 trillion total parameters. We propose the MuonClip optimizer, which improves upon Muon with a novel QK-clip technique to address training instability while enjoying the advanced token efficiency of Muon. Based on MuonClip, K2 was pre-trained on 15.5 trillion tokens with zero loss spike. During post-training, K2 undergoes a multi-stage post-training process, highlighted by a large-scale agentic data synthesis pipeline and a joint reinforcement learning (RL) stage, where the model improves its capabilities through interactions with real and synthetic environments. Kimi K2 achieves state-of-the-art performance among open-source non-thinking models, with strengths in agentic capabilities. Notably, K2 obtains 66.1 on Tau2-Bench, 76.5 on ACEBench (En), 65.8 on SWE-Bench Verified, and 47.3 on SWE-Bench Multilingual -- surpassing most open and closed-sourced baselines in non-thinking settings. It also exhibits strong capabilities in coding, mathematics, and reasoning tasks, with a score of 53.7 on LiveCodeBench v6, 49.5 on AIME 2025, 75.1 on GPQA-Diamond, and 27.1 on OJBench, all without extended thinking. These results position Kimi K2 as one of the most capable open-source large language models to date, particularly in software engineering and agentic tasks. We release our base and post-trained model checkpoints to facilitate future research and applications of agentic intelligence.

Data Mixing Can Induce Phase Transitions in Knowledge Acquisition

Large Language Models (LLMs) are typically trained on data mixtures: most data come from web scrapes, while a small portion is curated from high-quality sources with dense domain-specific knowledge. In this paper, we show that when training LLMs on such data mixtures, knowledge acquisition from knowledge-dense datasets, unlike training exclusively on knowledge-dense data (arXiv:2404.05405), does not always follow a smooth scaling law but can exhibit phase transitions with respect to the mixing ratio and model size. Through controlled experiments on a synthetic biography dataset mixed with web-scraped data, we demonstrate that: (1) as we increase the model size to a critical value, the model suddenly transitions from memorizing very few to most of the biographies; (2) below a critical mixing ratio, the model memorizes almost nothing even with extensive training, but beyond this threshold, it rapidly memorizes more biographies. We attribute these phase transitions to a capacity allocation phenomenon: a model with bounded capacity must act like a knapsack problem solver to minimize the overall test loss, and the optimal allocation across datasets can change discontinuously as the model size or mixing ratio varies. We formalize this intuition in an information-theoretic framework and reveal that these phase transitions are predictable, with the critical mixing ratio following a power-law relationship with the model size. Our findings highlight a concrete case where a good mixing recipe for large models may not be optimal for small models, and vice versa.

Keeping LLMs Aligned After Fine-tuning: The Crucial Role of Prompt Templates

Public LLMs such as the Llama 2-Chat have driven huge activity in LLM research. These models underwent alignment training and were considered safe. Recently Qi et al. (2023) reported that even benign fine-tuning (e.g., on seemingly safe datasets) can give rise to unsafe behaviors in the models. The current paper is about methods and best practices to mitigate such loss of alignment. Through extensive experiments on several chat models (Meta's Llama 2-Chat, Mistral AI's Mistral 7B Instruct v0.2, and OpenAI's GPT-3.5 Turbo), this paper uncovers that the prompt templates used during fine-tuning and inference play a crucial role in preserving safety alignment, and proposes the "Pure Tuning, Safe Testing" (PTST) principle -- fine-tune models without a safety prompt, but include it at test time. Fine-tuning experiments on GSM8K, ChatDoctor, and OpenOrca show that PTST significantly reduces the rise of unsafe behaviors, and even almost eliminates them in some cases.

A Quadratic Synchronization Rule for Distributed Deep Learning

In distributed deep learning with data parallelism, synchronizing gradients at each training step can cause a huge communication overhead, especially when many nodes work together to train large models. Local gradient methods, such as Local SGD, address this issue by allowing workers to compute locally for $H$ steps without synchronizing with others, hence reducing communication frequency. While $H$ has been viewed as a hyperparameter to trade optimization efficiency for communication cost, recent research indicates that setting a proper $H$ value can lead to generalization improvement. Yet, selecting a proper $H$ is elusive. This work proposes a theory-grounded method for determining $H$, named the Quadratic Synchronization Rule (QSR), which recommends dynamically setting $H$ in proportion to $\frac{1}{\eta^2}$ as the learning rate $\eta$ decays over time. Extensive ImageNet experiments on ResNet and ViT show that local gradient methods with QSR consistently improve the test accuracy over other synchronization strategies. Compared with the standard data parallel training, QSR enables Local AdamW on ViT-B to cut the training time on 16 or 64 GPUs down from 26.7 to 20.2 hours or from 8.6 to 5.5 hours and, at the same time, achieves $1.16\%$ or $0.84\%$ higher top-1 validation accuracy.

Why does Local SGD Generalize Better than SGD?

Local SGD is a communication-efficient variant of SGD for large-scale training, where multiple GPUs perform SGD independently and average the model parameters periodically. It has been recently observed that Local SGD can not only achieve the design goal of reducing the communication overhead but also lead to higher test accuracy than the corresponding SGD baseline (Lin et al., 2020b), though the training regimes for this to happen are still in debate (Ortiz et al., 2021). This paper aims to understand why (and when) Local SGD generalizes better based on Stochastic Differential Equation (SDE) approximation. The main contributions of this paper include (i) the derivation of an SDE that captures the long-term behavior of Local SGD in the small learning rate regime, showing how noise drives the iterate to drift and diffuse after it has reached close to the manifold of local minima, (ii) a comparison between the SDEs of Local SGD and SGD, showing that Local SGD induces a stronger drift term that can result in a stronger effect of regularization, e.g., a faster reduction of sharpness, and (iii) empirical evidence validating that having a small learning rate and long enough training time enables the generalization improvement over SGD but removing either of the two conditions leads to no improvement.

Fast Federated Learning in the Presence of Arbitrary Device Unavailability

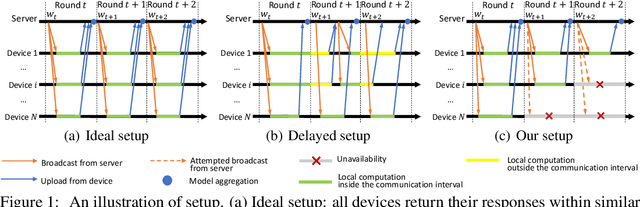
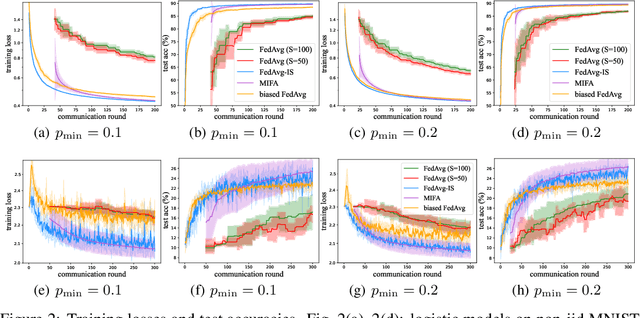
Federated Learning (FL) coordinates with numerous heterogeneous devices to collaboratively train a shared model while preserving user privacy. Despite its multiple advantages, FL faces new challenges. One challenge arises when devices drop out of the training process beyond the control of the central server. In this case, the convergence of popular FL algorithms such as FedAvg is severely influenced by the straggling devices. To tackle this challenge, we study federated learning algorithms under arbitrary device unavailability and propose an algorithm named Memory-augmented Impatient Federated Averaging (MIFA). Our algorithm efficiently avoids excessive latency induced by inactive devices, and corrects the gradient bias using the memorized latest updates from the devices. We prove that MIFA achieves minimax optimal convergence rates on non-i.i.d. data for both strongly convex and non-convex smooth functions. We also provide an explicit characterization of the improvement over baseline algorithms through a case study, and validate the results by numerical experiments on real-world datasets.