Why Does Sharpness-Aware Minimization Generalize Better Than SGD?

The challenge of overfitting, in which the model memorizes the training data and fails to generalize to test data, has become increasingly significant in the training of large neural networks. To tackle this challenge, Sharpness-Aware Minimization (SAM) has emerged as a promising training method, which can improve the generalization of neural networks even in the presence of label noise. However, a deep understanding of how SAM works, especially in the setting of nonlinear neural networks and classification tasks, remains largely missing. This paper fills this gap by demonstrating why SAM generalizes better than Stochastic Gradient Descent (SGD) for a certain data model and two-layer convolutional ReLU networks. The loss landscape of our studied problem is nonsmooth, thus current explanations for the success of SAM based on the Hessian information are insufficient. Our result explains the benefits of SAM, particularly its ability to prevent noise learning in the early stages, thereby facilitating more effective learning of features. Experiments on both synthetic and real data corroborate our theory.

Understanding Transferable Representation Learning and Zero-shot Transfer in CLIP

Multi-modal learning has become increasingly popular due to its ability to leverage information from different data sources (e.g., text and images) to improve the model performance. Recently, CLIP has emerged as an effective approach that employs vision-language contrastive pretraining to learn joint image and text representations and exhibits remarkable performance in zero-shot learning and text-guided natural image generation. Despite the huge practical success of CLIP, its theoretical understanding remains elusive. In this paper, we formally study transferrable representation learning underlying CLIP and demonstrate how features from different modalities get aligned. We also analyze its zero-shot transfer performance on the downstream tasks. Inspired by our analysis, we propose a new CLIP-type approach, which achieves better performance than CLIP and other state-of-the-art methods on benchmark datasets.

Benign Overfitting for Two-layer ReLU Networks

Modern deep learning models with great expressive power can be trained to overfit the training data but still generalize well. This phenomenon is referred to as benign overfitting. Recently, a few studies have attempted to theoretically understand benign overfitting in neural networks. However, these works are either limited to neural networks with smooth activation functions or to the neural tangent kernel regime. How and when benign overfitting can occur in ReLU neural networks remains an open problem. In this work, we seek to answer this question by establishing algorithm-dependent risk bounds for learning two-layer ReLU convolutional neural networks with label-flipping noise. We show that, under mild conditions, the neural network trained by gradient descent can achieve near-zero training loss and Bayes optimal test risk. Our result also reveals a sharp transition between benign and harmful overfitting under different conditions on data distribution in terms of test risk. Experiments on synthetic data back up our theory.

Learning High-Dimensional Single-Neuron ReLU Networks with Finite Samples

This paper considers the problem of learning a single ReLU neuron with squared loss (a.k.a., ReLU regression) in the overparameterized regime, where the input dimension can exceed the number of samples. We analyze a Perceptron-type algorithm called GLM-tron (Kakade et al., 2011), and provide its dimension-free risk upper bounds for high-dimensional ReLU regression in both well-specified and misspecified settings. Our risk bounds recover several existing results as special cases. Moreover, in the well-specified setting, we also provide an instance-wise matching risk lower bound for GLM-tron. Our upper and lower risk bounds provide a sharp characterization of the high-dimensional ReLU regression problems that can be learned via GLM-tron. On the other hand, we provide some negative results for stochastic gradient descent (SGD) for ReLU regression with symmetric Bernoulli data: if the model is well-specified, the excess risk of SGD is provably no better than that of GLM-tron ignoring constant factors, for each problem instance; and in the noiseless case, GLM-tron can achieve a small risk while SGD unavoidably suffers from a constant risk in expectation. These results together suggest that GLM-tron might be preferable than SGD for high-dimensional ReLU regression.

ISA-Net: Improved spatial attention network for PET-CT tumor segmentation

Achieving accurate and automated tumor segmentation plays an important role in both clinical practice and radiomics research. Segmentation in medicine is now often performed manually by experts, which is a laborious, expensive and error-prone task. Manual annotation relies heavily on the experience and knowledge of these experts. In addition, there is much intra- and interobserver variation. Therefore, it is of great significance to develop a method that can automatically segment tumor target regions. In this paper, we propose a deep learning segmentation method based on multimodal positron emission tomography-computed tomography (PET-CT), which combines the high sensitivity of PET and the precise anatomical information of CT. We design an improved spatial attention network(ISA-Net) to increase the accuracy of PET or CT in detecting tumors, which uses multi-scale convolution operation to extract feature information and can highlight the tumor region location information and suppress the non-tumor region location information. In addition, our network uses dual-channel inputs in the coding stage and fuses them in the decoding stage, which can take advantage of the differences and complementarities between PET and CT. We validated the proposed ISA-Net method on two clinical datasets, a soft tissue sarcoma(STS) and a head and neck tumor(HECKTOR) dataset, and compared with other attention methods for tumor segmentation. The DSC score of 0.8378 on STS dataset and 0.8076 on HECKTOR dataset show that ISA-Net method achieves better segmentation performance and has better generalization. Conclusions: The method proposed in this paper is based on multi-modal medical image tumor segmentation, which can effectively utilize the difference and complementarity of different modes. The method can also be applied to other multi-modal data or single-modal data by proper adjustment.

A General Framework for Sample-Efficient Function Approximation in Reinforcement Learning

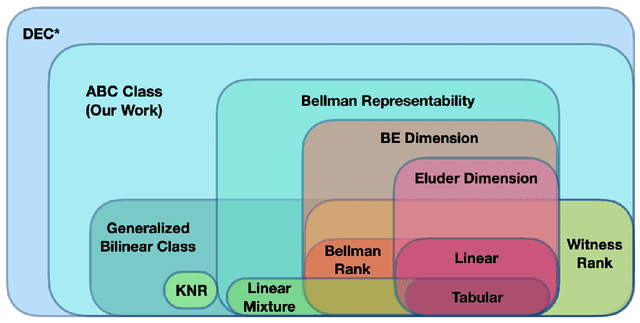
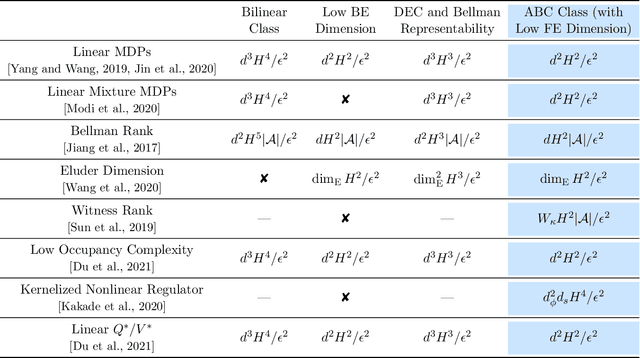
With the increasing need for handling large state and action spaces, general function approximation has become a key technique in reinforcement learning (RL). In this paper, we propose a general framework that unifies model-based and model-free RL, and an Admissible Bellman Characterization (ABC) class that subsumes nearly all Markov Decision Process (MDP) models in the literature for tractable RL. We propose a novel estimation function with decomposable structural properties for optimization-based exploration and the functional eluder dimension as a complexity measure of the ABC class. Under our framework, a new sample-efficient algorithm namely OPtimization-based ExploRation with Approximation (OPERA) is proposed, achieving regret bounds that match or improve over the best-known results for a variety of MDP models. In particular, for MDPs with low Witness rank, under a slightly stronger assumption, OPERA improves the state-of-the-art sample complexity results by a factor of $dH$. Our framework provides a generic interface to design and analyze new RL models and algorithms.

Towards Understanding Mixture of Experts in Deep Learning

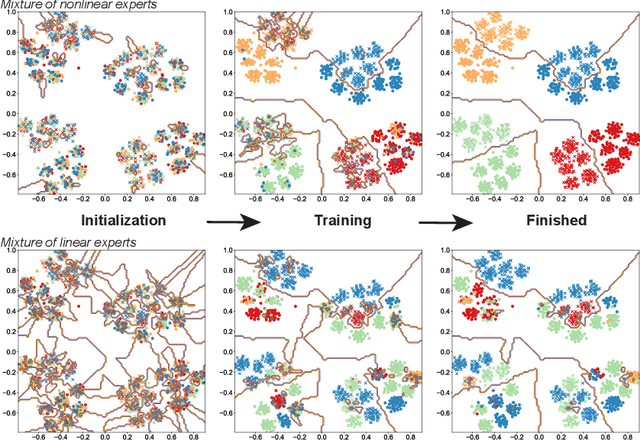
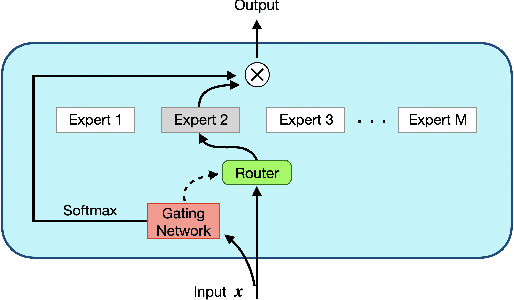
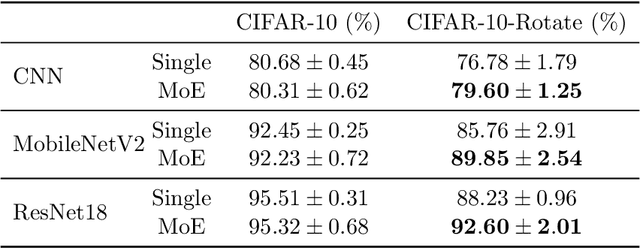
The Mixture-of-Experts (MoE) layer, a sparsely-activated model controlled by a router, has achieved great success in deep learning. However, the understanding of such architecture remains elusive. In this paper, we formally study how the MoE layer improves the performance of neural network learning and why the mixture model will not collapse into a single model. Our empirical results suggest that the cluster structure of the underlying problem and the non-linearity of the expert are pivotal to the success of MoE. To further understand this, we consider a challenging classification problem with intrinsic cluster structures, which is hard to learn using a single expert. Yet with the MoE layer, by choosing the experts as two-layer nonlinear convolutional neural networks (CNNs), we show that the problem can be learned successfully. Furthermore, our theory shows that the router can learn the cluster-center features, which helps divide the input complex problem into simpler linear classification sub-problems that individual experts can conquer. To our knowledge, this is the first result towards formally understanding the mechanism of the MoE layer for deep learning.

Benign Overfitting in Two-layer Convolutional Neural Networks

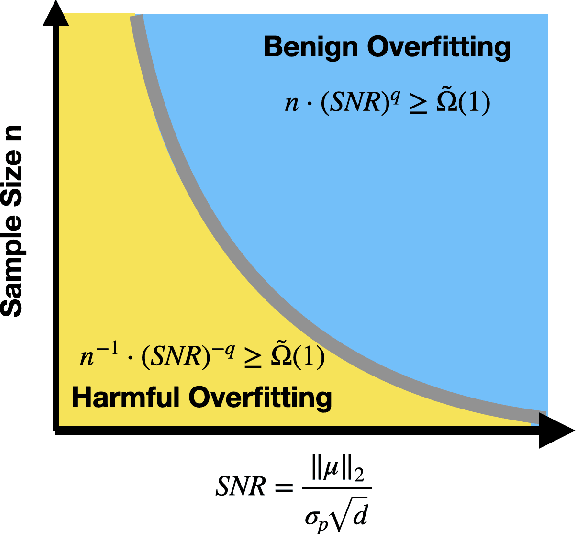
Modern neural networks often have great expressive power and can be trained to overfit the training data, while still achieving a good test performance. This phenomenon is referred to as "benign overfitting". Recently, there emerges a line of works studying "benign overfitting" from the theoretical perspective. However, they are limited to linear models or kernel/random feature models, and there is still a lack of theoretical understanding about when and how benign overfitting occurs in neural networks. In this paper, we study the benign overfitting phenomenon in training a two-layer convolutional neural network (CNN). We show that when the signal-to-noise ratio satisfies a certain condition, a two-layer CNN trained by gradient descent can achieve arbitrarily small training and test loss. On the other hand, when this condition does not hold, overfitting becomes harmful and the obtained CNN can only achieve constant level test loss. These together demonstrate a sharp phase transition between benign overfitting and harmful overfitting, driven by the signal-to-noise ratio. To the best of our knowledge, this is the first work that precisely characterizes the conditions under which benign overfitting can occur in training convolutional neural networks.

Faster Perturbed Stochastic Gradient Methods for Finding Local Minima

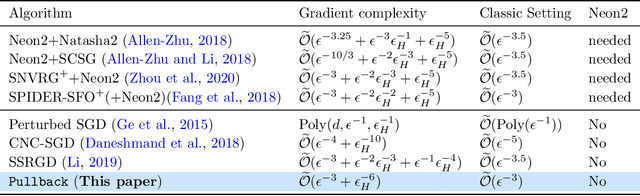
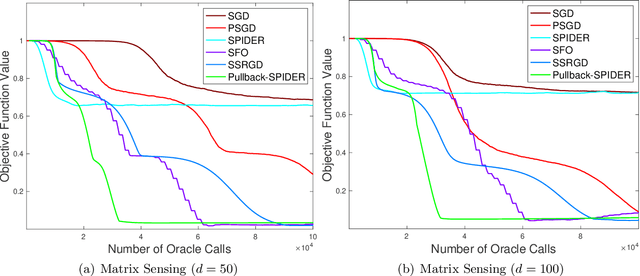
Escaping from saddle points and finding local minima is a central problem in nonconvex optimization. Perturbed gradient methods are perhaps the simplest approach for this problem. However, to find $(\epsilon, \sqrt{\epsilon})$-approximate local minima, the existing best stochastic gradient complexity for this type of algorithms is $\tilde O(\epsilon^{-3.5})$, which is not optimal. In this paper, we propose \texttt{Pullback}, a faster perturbed stochastic gradient framework for finding local minima. We show that Pullback with stochastic gradient estimators such as SARAH/SPIDER and STORM can find $(\epsilon, \epsilon_{H})$-approximate local minima within $\tilde O(\epsilon^{-3} + \epsilon_{H}^{-6})$ stochastic gradient evaluations (or $\tilde O(\epsilon^{-3})$ when $\epsilon_H = \sqrt{\epsilon}$). The core idea of our framework is a step-size ``pullback'' scheme to control the average movement of the iterates, which leads to faster convergence to the local minima. Experiments on matrix factorization problems corroborate our theory.

Self-training Converts Weak Learners to Strong Learners in Mixture Models

We consider a binary classification problem when the data comes from a mixture of two isotropic distributions satisfying concentration and anti-concentration properties enjoyed by log-concave distributions among others. We show that there exists a universal constant $C_{\mathrm{err}}>0$ such that if a pseudolabeler $\boldsymbol{\beta}_{\mathrm{pl}}$ can achieve classification error at most $C_{\mathrm{err}}$, then for any $\varepsilon>0$, an iterative self-training algorithm initialized at $\boldsymbol{\beta}_0 := \boldsymbol{\beta}_{\mathrm{pl}}$ using pseudolabels $\hat y = \mathrm{sgn}(\langle \boldsymbol{\beta}_t, \mathbf{x}\rangle)$ and using at most $\tilde O(d/\varepsilon^2)$ unlabeled examples suffices to learn the Bayes-optimal classifier up to $\varepsilon$ error, where $d$ is the ambient dimension. That is, self-training converts weak learners to strong learners using only unlabeled examples. We additionally show that by running gradient descent on the logistic loss one can obtain a pseudolabeler $\boldsymbol{\beta}_{\mathrm{pl}}$ with classification error $C_{\mathrm{err}}$ using only $O(d)$ labeled examples (i.e., independent of $\varepsilon$). Together our results imply that mixture models can be learned to within $\varepsilon$ of the Bayes-optimal accuracy using at most $O(d)$ labeled examples and $\tilde O(d/\varepsilon^2)$ unlabeled examples by way of a semi-supervised self-training algorithm.