Online Learning with Limited Information in the Sliding Window Model

Motivated by recent work on the experts problem in the streaming model, we consider the experts problem in the sliding window model. The sliding window model is a well-studied model that captures applications such as traffic monitoring, epidemic tracking, and automated trading, where recent information is more valuable than older data. Formally, we have $n$ experts, $T$ days, the ability to query the predictions of $q$ experts on each day, a limited amount of memory, and should achieve the (near-)optimal regret $\sqrt{nW}\text{polylog}(nT)$ regret over any window of the last $W$ days. While it is impossible to achieve such regret with $1$ query, we show that with $2$ queries we can achieve such regret and with only $\text{polylog}(nT)$ bits of memory. Not only are our algorithms optimal for sliding windows, but we also show for every interval $\mathcal{I}$ of days that we achieve $\sqrt{n|\mathcal{I}|}\text{polylog}(nT)$ regret with $2$ queries and only $\text{polylog}(nT)$ bits of memory, providing an exponential improvement on the memory of previous interval regret algorithms. Building upon these techniques, we address the bandit problem in data streams, where $q=1$, achieving $n T^{2/3}\text{polylog}(T)$ regret with $\text{polylog}(nT)$ memory, which is the first sublinear regret in the streaming model in the bandit setting with polylogarithmic memory; this can be further improved to the optimal $\mathcal{O}(\sqrt{nT})$ regret if the best expert's losses are in a random order.

Support Basis: Fast Attention Beyond Bounded Entries

The quadratic complexity of softmax attention remains a central bottleneck in scaling large language models (LLMs). [Alman and Song, NeurIPS 2023] proposed a sub-quadratic attention approximation algorithm, but it works only under the restrictive bounded-entry assumption. Since this assumption rarely holds in practice, its applicability to modern LLMs is limited. In this paper, we introduce support-basis decomposition, a new framework for efficient attention approximation beyond bounded entries. We empirically demonstrate that the entries of the query and key matrices exhibit sub-Gaussian behavior. Our approach uses this property to split large and small entries, enabling exact computation on sparse components and polynomial approximation on dense components. We establish rigorous theoretical guarantees, proving a sub-quadratic runtime, and extend the method to a multi-threshold setting that eliminates all distributional assumptions. Furthermore, we provide the first theoretical justification for the empirical success of polynomial attention [Kacham, Mirrokni, and Zhong, ICML 2024], showing that softmax attention can be closely approximated by a combination of multiple polynomial attentions with sketching.

Learning-Augmented Hierarchical Clustering

Hierarchical clustering (HC) is an important data analysis technique in which the goal is to recursively partition a dataset into a tree-like structure while grouping together similar data points at each level of granularity. Unfortunately, for many of the proposed HC objectives, there exist strong barriers to approximation algorithms with the hardness of approximation. Thus, we consider the problem of hierarchical clustering given auxiliary information from natural oracles. Specifically, we focus on a *splitting oracle* which, when provided with a triplet of vertices $(u,v,w)$, answers (possibly erroneously) the pairs of vertices whose lowest common ancestor includes all three vertices in an optimal tree, i.e., identifying which vertex ``splits away'' from the others. Using such an oracle, we obtain the following results: - A polynomial-time algorithm that outputs a hierarchical clustering tree with $O(1)$-approximation to the Dasgupta objective (Dasgupta [STOC'16]). - A near-linear time algorithm that outputs a hierarchical clustering tree with $(1-o(1))$-approximation to the Moseley-Wang objective (Moseley and Wang [NeurIPS'17]). Under the plausible Small Set Expansion Hypothesis, no polynomial-time algorithm can achieve any constant approximation for Dasgupta's objective or $(1-C)$-approximation for the Moseley-Wang objective for some constant $C>0$. As such, our results demonstrate that the splitting oracle enables algorithms to outperform standard HC approaches and overcome hardness constraints. Furthermore, our approaches extend to sublinear settings, in which we show new streaming and PRAM algorithms for HC with improved guarantees.

AutoL2S: Auto Long-Short Reasoning for Efficient Large Language Models

The reasoning-capable large language models (LLMs) demonstrate strong performance on complex reasoning tasks but often suffer from overthinking, generating unnecessarily long chain-of-thought (CoT) reasoning paths for easy reasoning questions, thereby increasing inference cost and latency. Recent approaches attempt to address this challenge by manually deciding when to apply long or short reasoning. However, they lack the flexibility to adapt CoT length dynamically based on question complexity. In this paper, we propose Auto Long-Short Reasoning (AutoL2S), a dynamic and model-agnostic framework that enables LLMs to dynamically compress their generated reasoning path based on the complexity of the reasoning question. AutoL2S enables a learned paradigm, in which LLMs themselves can decide when longer reasoning is necessary and when shorter reasoning suffices, by training on data annotated with our proposed method, which includes both long and short CoT paths and a special <EASY> token. We then use <EASY> token to indicate when the model can skip generating lengthy CoT reasoning. This proposed annotation strategy can enhance the LLMs' ability to generate shorter CoT reasoning paths with improved quality after training. Extensive evaluation results show that AutoL2S reduces the length of reasoning generation by up to 57% without compromising performance, demonstrating the effectiveness of AutoL2S for scalable and efficient LLM reasoning.

Memory-Statistics Tradeoff in Continual Learning with Structural Regularization

We study the statistical performance of a continual learning problem with two linear regression tasks in a well-specified random design setting. We consider a structural regularization algorithm that incorporates a generalized $\ell_2$-regularization tailored to the Hessian of the previous task for mitigating catastrophic forgetting. We establish upper and lower bounds on the joint excess risk for this algorithm. Our analysis reveals a fundamental trade-off between memory complexity and statistical efficiency, where memory complexity is measured by the number of vectors needed to define the structural regularization. Specifically, increasing the number of vectors in structural regularization leads to a worse memory complexity but an improved excess risk, and vice versa. Furthermore, our theory suggests that naive continual learning without regularization suffers from catastrophic forgetting, while structural regularization mitigates this issue. Notably, structural regularization achieves comparable performance to joint training with access to both tasks simultaneously. These results highlight the critical role of curvature-aware regularization for continual learning.

I3S: Importance Sampling Subspace Selection for Low-Rank Optimization in LLM Pretraining

Low-rank optimization has emerged as a promising approach to enabling memory-efficient training of large language models (LLMs). Existing low-rank optimization methods typically project gradients onto a low-rank subspace, reducing the memory cost of storing optimizer states. A key challenge in these methods is identifying suitable subspaces to ensure an effective optimization trajectory. Most existing approaches select the dominant subspace to preserve gradient information, as this intuitively provides the best approximation. However, we find that in practice, the dominant subspace stops changing during pretraining, thereby constraining weight updates to similar subspaces. In this paper, we propose importance sampling subspace selection (I3S) for low-rank optimization, which theoretically offers a comparable convergence rate to the dominant subspace approach. Empirically, we demonstrate that I3S significantly outperforms previous methods in LLM pretraining tasks.

Confident or Seek Stronger: Exploring Uncertainty-Based On-device LLM Routing From Benchmarking to Generalization

Large language models (LLMs) are increasingly deployed and democratized on edge devices. To improve the efficiency of on-device deployment, small language models (SLMs) are often adopted due to their efficient decoding latency and reduced energy consumption. However, these SLMs often generate inaccurate responses when handling complex queries. One promising solution is uncertainty-based SLM routing, offloading high-stakes queries to stronger LLMs when resulting in low-confidence responses on SLM. This follows the principle of "If you lack confidence, seek stronger support" to enhance reliability. Relying on more powerful LLMs is yet effective but increases invocation costs. Therefore, striking a routing balance between efficiency and efficacy remains a critical challenge. Additionally, efficiently generalizing the routing strategy to new datasets remains under-explored. In this paper, we conduct a comprehensive investigation into benchmarking and generalization of uncertainty-driven routing strategies from SLMs to LLMs over 1500+ settings. Our findings highlight: First, uncertainty-correctness alignment in different uncertainty quantification (UQ) methods significantly impacts routing performance. Second, uncertainty distributions depend more on both the specific SLM and the chosen UQ method, rather than downstream data. Building on the insight, we propose a calibration data construction instruction pipeline and open-source a constructed hold-out set to enhance routing generalization on new downstream scenarios. The experimental results indicate calibration data effectively bootstraps routing performance without any new data.

Towards Fair Medical AI: Adversarial Debiasing of 3D CT Foundation Embeddings

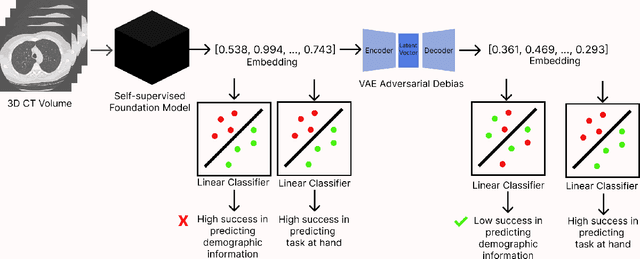
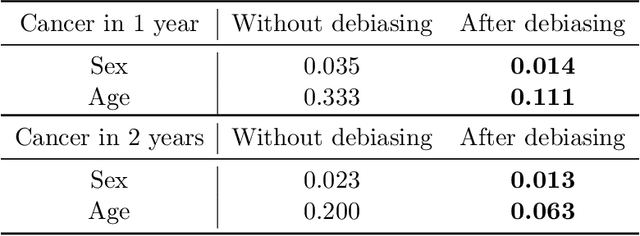
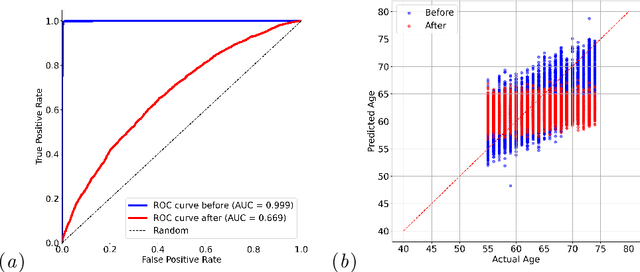
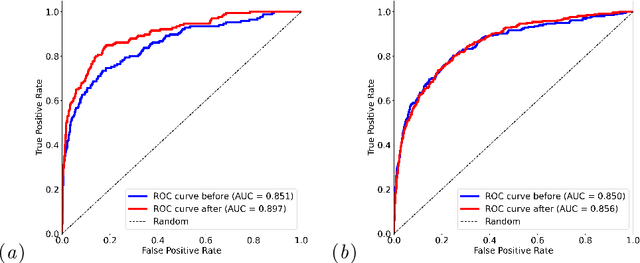
Self-supervised learning has revolutionized medical imaging by enabling efficient and generalizable feature extraction from large-scale unlabeled datasets. Recently, self-supervised foundation models have been extended to three-dimensional (3D) computed tomography (CT) data, generating compact, information-rich embeddings with 1408 features that achieve state-of-the-art performance on downstream tasks such as intracranial hemorrhage detection and lung cancer risk forecasting. However, these embeddings have been shown to encode demographic information, such as age, sex, and race, which poses a significant risk to the fairness of clinical applications. In this work, we propose a Variation Autoencoder (VAE) based adversarial debiasing framework to transform these embeddings into a new latent space where demographic information is no longer encoded, while maintaining the performance of critical downstream tasks. We validated our approach on the NLST lung cancer screening dataset, demonstrating that the debiased embeddings effectively eliminate multiple encoded demographic information and improve fairness without compromising predictive accuracy for lung cancer risk at 1-year and 2-year intervals. Additionally, our approach ensures the embeddings are robust against adversarial bias attacks. These results highlight the potential of adversarial debiasing techniques to ensure fairness and equity in clinical applications of self-supervised 3D CT embeddings, paving the way for their broader adoption in unbiased medical decision-making.

Fully Dynamic Adversarially Robust Correlation Clustering in Polylogarithmic Update Time

We study the dynamic correlation clustering problem with $\textit{adaptive}$ edge label flips. In correlation clustering, we are given a $n$-vertex complete graph whose edges are labeled either $(+)$ or $(-)$, and the goal is to minimize the total number of $(+)$ edges between clusters and the number of $(-)$ edges within clusters. We consider the dynamic setting with adversarial robustness, in which the $\textit{adaptive}$ adversary could flip the label of an edge based on the current output of the algorithm. Our main result is a randomized algorithm that always maintains an $O(1)$-approximation to the optimal correlation clustering with $O(\log^{2}{n})$ amortized update time. Prior to our work, no algorithm with $O(1)$-approximation and $\text{polylog}{(n)}$ update time for the adversarially robust setting was known. We further validate our theoretical results with experiments on synthetic and real-world datasets with competitive empirical performances. Our main technical ingredient is an algorithm that maintains $\textit{sparse-dense decomposition}$ with $\text{polylog}{(n)}$ update time, which could be of independent interest.

Federated Learning Clients Clustering with Adaptation to Data Drifts

Federated Learning (FL) enables deep learning model training across edge devices and protects user privacy by retaining raw data locally. Data heterogeneity in client distributions slows model convergence and leads to plateauing with reduced precision. Clustered FL solutions address this by grouping clients with statistically similar data and training models for each cluster. However, maintaining consistent client similarity within each group becomes challenging when data drifts occur, significantly impacting model accuracy. In this paper, we introduce Fielding, a clustered FL framework that handles data drifts promptly with low overheads. Fielding detects drifts on all clients and performs selective label distribution-based re-clustering to balance cluster optimality and model performance, remaining robust to malicious clients and varied heterogeneity degrees. Our evaluations show that Fielding improves model final accuracy by 1.9%-5.9% and reaches target accuracies 1.16x-2.61x faster.