Humanizing the Machine: Proxy Attacks to Mislead LLM Detectors

The advent of large language models (LLMs) has revolutionized the field of text generation, producing outputs that closely mimic human-like writing. Although academic and industrial institutions have developed detectors to prevent the malicious usage of LLM-generated texts, other research has doubt about the robustness of these systems. To stress test these detectors, we introduce a proxy-attack strategy that effortlessly compromises LLMs, causing them to produce outputs that align with human-written text and mislead detection systems. Our method attacks the source model by leveraging a reinforcement learning (RL) fine-tuned humanized small language model (SLM) in the decoding phase. Through an in-depth analysis, we demonstrate that our attack strategy is capable of generating responses that are indistinguishable to detectors, preventing them from differentiating between machine-generated and human-written text. We conduct systematic evaluations on extensive datasets using proxy-attacked open-source models, including Llama2-13B, Llama3-70B, and Mixtral-8*7B in both white- and black-box settings. Our findings show that the proxy-attack strategy effectively deceives the leading detectors, resulting in an average AUROC drop of 70.4% across multiple datasets, with a maximum drop of 90.3% on a single dataset. Furthermore, in cross-discipline scenarios, our strategy also bypasses these detectors, leading to a significant relative decrease of up to 90.9%, while in cross-language scenario, the drop reaches 91.3%. Despite our proxy-attack strategy successfully bypassing the detectors with such significant relative drops, we find that the generation quality of the attacked models remains preserved, even within a modest utility budget, when compared to the text produced by the original, unattacked source model.

Physics-Informed Regularization for Domain-Agnostic Dynamical System Modeling

Learning complex physical dynamics purely from data is challenging due to the intrinsic properties of systems to be satisfied. Incorporating physics-informed priors, such as in Hamiltonian Neural Networks (HNNs), achieves high-precision modeling for energy-conservative systems. However, real-world systems often deviate from strict energy conservation and follow different physical priors. To address this, we present a framework that achieves high-precision modeling for a wide range of dynamical systems from the numerical aspect, by enforcing Time-Reversal Symmetry (TRS) via a novel regularization term. It helps preserve energies for conservative systems while serving as a strong inductive bias for non-conservative, reversible systems. While TRS is a domain-specific physical prior, we present the first theoretical proof that TRS loss can universally improve modeling accuracy by minimizing higher-order Taylor terms in ODE integration, which is numerically beneficial to various systems regardless of their properties, even for irreversible systems. By integrating the TRS loss within neural ordinary differential equation models, the proposed model TREAT demonstrates superior performance on diverse physical systems. It achieves a significant 11.5% MSE improvement in a challenging chaotic triple-pendulum scenario, underscoring TREAT's broad applicability and effectiveness.

Improving Logits-based Detector without Logits from Black-box LLMs

The advent of Large Language Models (LLMs) has revolutionized text generation, producing outputs that closely mimic human writing. This blurring of lines between machine- and human-written text presents new challenges in distinguishing one from the other a task further complicated by the frequent updates and closed nature of leading proprietary LLMs. Traditional logits-based detection methods leverage surrogate models for identifying LLM-generated content when the exact logits are unavailable from black-box LLMs. However, these methods grapple with the misalignment between the distributions of the surrogate and the often undisclosed target models, leading to performance degradation, particularly with the introduction of new, closed-source models. Furthermore, while current methodologies are generally effective when the source model is identified, they falter in scenarios where the model version remains unknown, or the test set comprises outputs from various source models. To address these limitations, we present Distribution-Aligned LLMs Detection (DALD), an innovative framework that redefines the state-of-the-art performance in black-box text detection even without logits from source LLMs. DALD is designed to align the surrogate model's distribution with that of unknown target LLMs, ensuring enhanced detection capability and resilience against rapid model iterations with minimal training investment. By leveraging corpus samples from publicly accessible outputs of advanced models such as ChatGPT, GPT-4 and Claude-3, DALD fine-tunes surrogate models to synchronize with unknown source model distributions effectively.

TANGO: Time-Reversal Latent GraphODE for Multi-Agent Dynamical Systems

Learning complex multi-agent system dynamics from data is crucial across many domains, such as in physical simulations and material modeling. Extended from purely data-driven approaches, existing physics-informed approaches such as Hamiltonian Neural Network strictly follow energy conservation law to introduce inductive bias, making their learning more sample efficiently. However, many real-world systems do not strictly conserve energy, such as spring systems with frictions. Recognizing this, we turn our attention to a broader physical principle: Time-Reversal Symmetry, which depicts that the dynamics of a system shall remain invariant when traversed back over time. It still helps to preserve energies for conservative systems and in the meanwhile, serves as a strong inductive bias for non-conservative, reversible systems. To inject such inductive bias, in this paper, we propose a simple-yet-effective self-supervised regularization term as a soft constraint that aligns the forward and backward trajectories predicted by a continuous graph neural network-based ordinary differential equation (GraphODE). It effectively imposes time-reversal symmetry to enable more accurate model predictions across a wider range of dynamical systems under classical mechanics. In addition, we further provide theoretical analysis to show that our regularization essentially minimizes higher-order Taylor expansion terms during the ODE integration steps, which enables our model to be more noise-tolerant and even applicable to irreversible systems. Experimental results on a variety of physical systems demonstrate the effectiveness of our proposed method. Particularly, it achieves an MSE improvement of 11.5 % on a challenging chaotic triple-pendulum systems.

Benign Overfitting for Two-layer ReLU Networks

Modern deep learning models with great expressive power can be trained to overfit the training data but still generalize well. This phenomenon is referred to as benign overfitting. Recently, a few studies have attempted to theoretically understand benign overfitting in neural networks. However, these works are either limited to neural networks with smooth activation functions or to the neural tangent kernel regime. How and when benign overfitting can occur in ReLU neural networks remains an open problem. In this work, we seek to answer this question by establishing algorithm-dependent risk bounds for learning two-layer ReLU convolutional neural networks with label-flipping noise. We show that, under mild conditions, the neural network trained by gradient descent can achieve near-zero training loss and Bayes optimal test risk. Our result also reveals a sharp transition between benign and harmful overfitting under different conditions on data distribution in terms of test risk. Experiments on synthetic data back up our theory.

Monocular Visual Analysis for Electronic Line Calling of Tennis Games

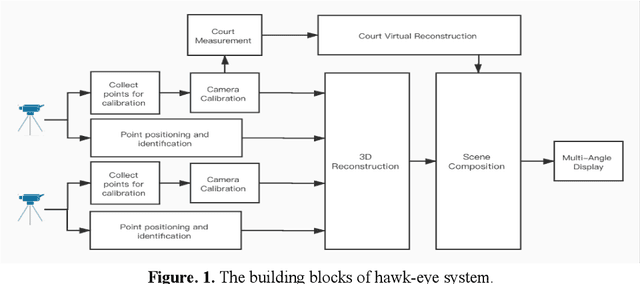
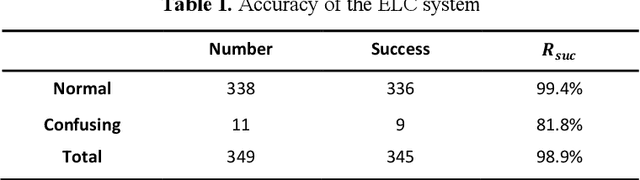
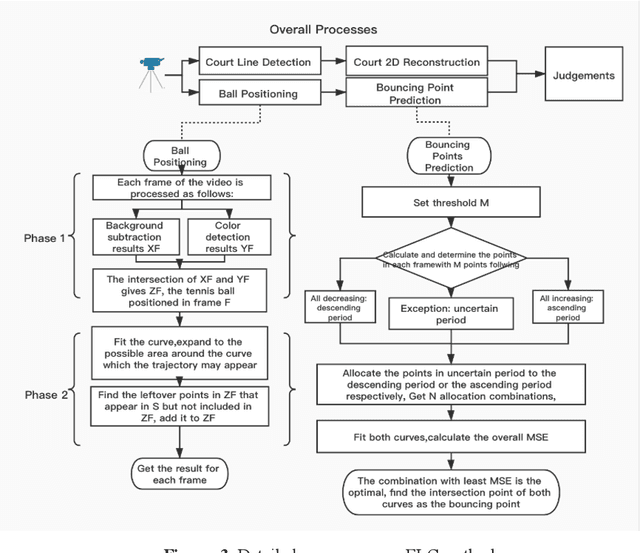
Electronic Line Calling is an auxiliary referee system used for tennis matches based on binocular vision technology. While ELC has been widely used, there are still many problems, such as complex installation and maintenance, high cost and etc. We propose a monocular vision technology based ELC method. The method has the following steps. First, locate the tennis ball's trajectory. We propose a multistage tennis ball positioning approach combining background subtraction and color area filtering. Then we propose a bouncing point prediction method by minimizing the fitting loss of the uncertain point. Finally, we find out whether the bouncing point of the ball is out of bounds or not according to the relative position between the bouncing point and the court side line in the two dimensional image. We collected and tagged 394 samples with an accuracy rate of 99.4%, and 81.8% of the 11 samples with bouncing points.The experimental results show that our method is feasible to judge if a ball is out of the court with monocular vision and significantly reduce complex installation and costs of ELC system with binocular vision.