Enhancing Stochastic Optimization for Statistical Efficiency Using ROOT-SGD with Diminishing Stepsize

In this paper, we revisit \textsf{ROOT-SGD}, an innovative method for stochastic optimization to bridge the gap between stochastic optimization and statistical efficiency. The proposed method enhances the performance and reliability of \textsf{ROOT-SGD} by integrating a carefully designed \emph{diminishing stepsize strategy}. This approach addresses key challenges in optimization, providing robust theoretical guarantees and practical benefits. Our analysis demonstrates that \textsf{ROOT-SGD} with diminishing achieves optimal convergence rates while maintaining computational efficiency. By dynamically adjusting the learning rate, \textsf{ROOT-SGD} ensures improved stability and precision throughout the optimization process. The findings of this study offer valuable insights for developing advanced optimization algorithms that are both efficient and statistically robust.

Fast Decentralized Gradient Tracking for Federated Minimax Optimization with Local Updates

Federated learning (FL) for minimax optimization has emerged as a powerful paradigm for training models across distributed nodes/clients while preserving data privacy and model robustness on data heterogeneity. In this work, we delve into the decentralized implementation of federated minimax optimization by proposing \texttt{K-GT-Minimax}, a novel decentralized minimax optimization algorithm that combines local updates and gradient tracking techniques. Our analysis showcases the algorithm's communication efficiency and convergence rate for nonconvex-strongly-concave (NC-SC) minimax optimization, demonstrating a superior convergence rate compared to existing methods. \texttt{K-GT-Minimax}'s ability to handle data heterogeneity and ensure robustness underscores its significance in advancing federated learning research and applications.

Accelerated Fully First-Order Methods for Bilevel and Minimax Optimization

This paper presents a new algorithm member for accelerating first-order methods for bilevel optimization, namely the \emph{(Perturbed) Restarted Accelerated Fully First-order methods for Bilevel Approximation}, abbreviated as \texttt{(P)RAF${}^2$BA}. The algorithm leverages \emph{fully} first-order oracles and seeks approximate stationary points in nonconvex-strongly-convex bilevel optimization, enhancing oracle complexity for efficient optimization. Theoretical guarantees for finding approximate first-order stationary points and second-order stationary points at the state-of-the-art query complexities are established, showcasing their effectiveness in solving complex optimization tasks. Empirical studies for real-world problems are provided to further validate the outperformance of our proposed algorithms. The significance of \texttt{(P)RAF${}^2$BA} in optimizing nonconvex-strongly-convex bilevel optimization problems is underscored by its state-of-the-art convergence rates and computational efficiency.

A General Continuous-Time Formulation of Stochastic ADMM and Its Variants

Stochastic versions of the alternating direction method of multiplier (ADMM) and its variants play a key role in many modern large-scale machine learning problems. In this work, we introduce a unified algorithmic framework called generalized stochastic ADMM and investigate their continuous-time analysis. The generalized framework widely includes many stochastic ADMM variants such as standard, linearized and gradient-based ADMM. Our continuous-time analysis provides us with new insights into stochastic ADMM and variants, and we rigorously prove that under some proper scaling, the trajectory of stochastic ADMM weakly converges to the solution of a stochastic differential equation with small noise. Our analysis also provides a theoretical explanation of why the relaxation parameter should be chosen between 0 and 2.

Accelerating Inexact HyperGradient Descent for Bilevel Optimization

We present a method for solving general nonconvex-strongly-convex bilevel optimization problems. Our method -- the \emph{Restarted Accelerated HyperGradient Descent} (\texttt{RAHGD}) method -- finds an $\epsilon$-first-order stationary point of the objective with $\tilde{\mathcal{O}}(\kappa^{3.25}\epsilon^{-1.75})$ oracle complexity, where $\kappa$ is the condition number of the lower-level objective and $\epsilon$ is the desired accuracy. We also propose a perturbed variant of \texttt{RAHGD} for finding an $\big(\epsilon,\mathcal{O}(\kappa^{2.5}\sqrt{\epsilon}\,)\big)$-second-order stationary point within the same order of oracle complexity. Our results achieve the best-known theoretical guarantees for finding stationary points in bilevel optimization and also improve upon the existing upper complexity bound for finding second-order stationary points in nonconvex-strongly-concave minimax optimization problems, setting a new state-of-the-art benchmark. Empirical studies are conducted to validate the theoretical results in this paper.

Nesterov Meets Optimism: Rate-Optimal Optimistic-Gradient-Based Method for Stochastic Bilinearly-Coupled Minimax Optimization

We provide a novel first-order optimization algorithm for bilinearly-coupled strongly-convex-concave minimax optimization called the AcceleratedGradient OptimisticGradient (AG-OG). The main idea of our algorithm is to leverage the structure of the considered minimax problem and operates Nesterov's acceleration on the individual part and optimistic gradient on the coupling part of the objective. We motivate our method by showing that its continuous-time dynamics corresponds to an organic combination of the dynamics of optimistic gradient and of Nesterov's acceleration. By discretizing the dynamics we conclude polynomial convergence behavior in discrete time. Further enhancement of AG-OG with proper restarting allows us to achieve rate-optimal (up to a constant) convergence rates with respect to the conditioning of the coupling and individual parts, which results in the first single-call algorithm achieving improved convergence in the deterministic setting and rate-optimality in the stochastic setting under bilinearly coupled minimax problem sets.

A General Framework for Sample-Efficient Function Approximation in Reinforcement Learning

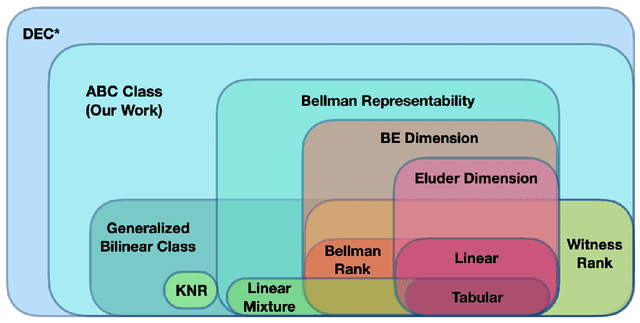
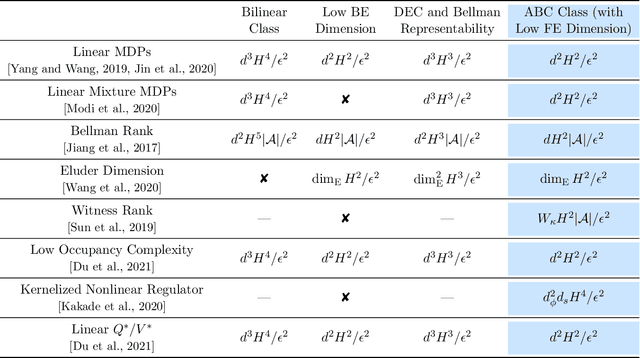
With the increasing need for handling large state and action spaces, general function approximation has become a key technique in reinforcement learning (RL). In this paper, we propose a general framework that unifies model-based and model-free RL, and an Admissible Bellman Characterization (ABC) class that subsumes nearly all Markov Decision Process (MDP) models in the literature for tractable RL. We propose a novel estimation function with decomposable structural properties for optimization-based exploration and the functional eluder dimension as a complexity measure of the ABC class. Under our framework, a new sample-efficient algorithm namely OPtimization-based ExploRation with Approximation (OPERA) is proposed, achieving regret bounds that match or improve over the best-known results for a variety of MDP models. In particular, for MDPs with low Witness rank, under a slightly stronger assumption, OPERA improves the state-of-the-art sample complexity results by a factor of $dH$. Our framework provides a generic interface to design and analyze new RL models and algorithms.

Learning Two-Player Mixture Markov Games: Kernel Function Approximation and Correlated Equilibrium

We consider learning Nash equilibria in two-player zero-sum Markov Games with nonlinear function approximation, where the action-value function is approximated by a function in a Reproducing Kernel Hilbert Space (RKHS). The key challenge is how to do exploration in the high-dimensional function space. We propose a novel online learning algorithm to find a Nash equilibrium by minimizing the duality gap. At the core of our algorithms are upper and lower confidence bounds that are derived based on the principle of optimism in the face of uncertainty. We prove that our algorithm is able to attain an $O(\sqrt{T})$ regret with polynomial computational complexity, under very mild assumptions on the reward function and the underlying dynamic of the Markov Games. We also propose several extensions of our algorithm, including an algorithm with Bernstein-type bonus that can achieve a tighter regret bound, and another algorithm for model misspecification that can be applied to neural function approximation.

Optimal Extragradient-Based Bilinearly-Coupled Saddle-Point Optimization

We consider the smooth convex-concave bilinearly-coupled saddle-point problem, $\min_{\mathbf{x}}\max_{\mathbf{y}}~F(\mathbf{x}) + H(\mathbf{x},\mathbf{y}) - G(\mathbf{y})$, where one has access to stochastic first-order oracles for $F$, $G$ as well as the bilinear coupling function $H$. Building upon standard stochastic extragradient analysis for variational inequalities, we present a stochastic \emph{accelerated gradient-extragradient (AG-EG)} descent-ascent algorithm that combines extragradient and Nesterov's acceleration in general stochastic settings. This algorithm leverages scheduled restarting to admit a fine-grained nonasymptotic convergence rate that matches known lower bounds by both \citet{ibrahim2020linear} and \citet{zhang2021lower} in their corresponding settings, plus an additional statistical error term for bounded stochastic noise that is optimal up to a constant prefactor. This is the first result that achieves such a relatively mature characterization of optimality in saddle-point optimization.

Nonconvex Stochastic Scaled-Gradient Descent and Generalized Eigenvector Problems

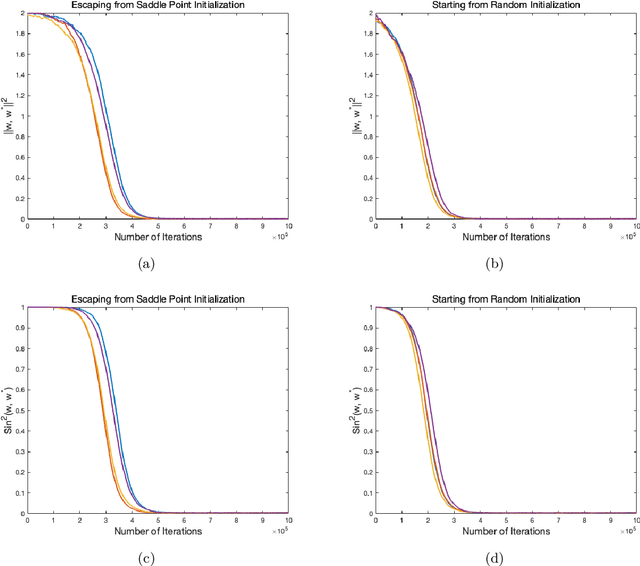
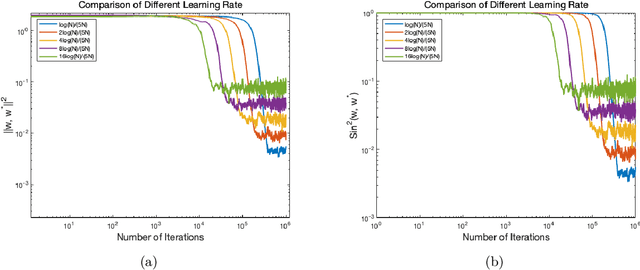
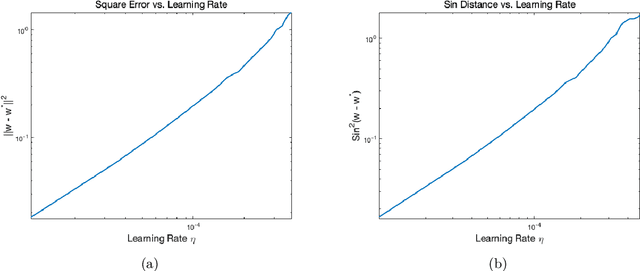
Motivated by the problem of online canonical correlation analysis, we propose the \emph{Stochastic Scaled-Gradient Descent} (SSGD) algorithm for minimizing the expectation of a stochastic function over a generic Riemannian manifold. SSGD generalizes the idea of projected stochastic gradient descent and allows the use of scaled stochastic gradients instead of stochastic gradients. In the special case of a spherical constraint, which arises in generalized eigenvector problems, we establish a nonasymptotic finite-sample bound of $\sqrt{1/T}$, and show that this rate is minimax optimal, up to a polylogarithmic factor of relevant parameters. On the asymptotic side, a novel trajectory-averaging argument allows us to achieve local asymptotic normality with a rate that matches that of Ruppert-Polyak-Juditsky averaging. We bring these ideas together in an application to online canonical correlation analysis, deriving, for the first time in the literature, an optimal one-time-scale algorithm with an explicit rate of local asymptotic convergence to normality. Numerical studies of canonical correlation analysis are also provided for synthetic data.