Differentiable Evolutionary Reinforcement Learning

The design of effective reward functions presents a central and often arduous challenge in reinforcement learning (RL), particularly when developing autonomous agents for complex reasoning tasks. While automated reward optimization approaches exist, they typically rely on derivative-free evolutionary heuristics that treat the reward function as a black box, failing to capture the causal relationship between reward structure and task performance. To bridge this gap, we propose Differentiable Evolutionary Reinforcement Learning (DERL), a bilevel framework that enables the autonomous discovery of optimal reward signals. In DERL, a Meta-Optimizer evolves a reward function (i.e., Meta-Reward) by composing structured atomic primitives, guiding the training of an inner-loop policy. Crucially, unlike previous evolution, DERL is differentiable in its metaoptimization: it treats the inner-loop validation performance as a signal to update the Meta-Optimizer via reinforcement learning. This allows DERL to approximate the "meta-gradient" of task success, progressively learning to generate denser and more actionable feedback. We validate DERL across three distinct domains: robotic agent (ALFWorld), scientific simulation (ScienceWorld), and mathematical reasoning (GSM8k, MATH). Experimental results show that DERL achieves state-of-the-art performance on ALFWorld and ScienceWorld, significantly outperforming methods relying on heuristic rewards, especially in out-of-distribution scenarios. Analysis of the evolutionary trajectory demonstrates that DERL successfully captures the intrinsic structure of tasks, enabling selfimproving agent alignment without human intervention.

Towards Theoretical Understanding of Transformer Test-Time Computing: Investigation on In-Context Linear Regression

Using more test-time computation during language model inference, such as generating more intermediate thoughts or sampling multiple candidate answers, has proven effective in significantly improving model performance. This paper takes an initial step toward bridging the gap between practical language model inference and theoretical transformer analysis by incorporating randomness and sampling. We focus on in-context linear regression with continuous/binary coefficients, where our framework simulates language model decoding through noise injection and binary coefficient sampling. Through this framework, we provide detailed analyses of widely adopted inference techniques. Supported by empirical results, our theoretical framework and analysis demonstrate the potential for offering new insights into understanding inference behaviors in real-world language models.

Self-Contradiction as Self-Improvement: Mitigating the Generation-Understanding Gap in MLLMs

Despite efforts to unify multimodal generation and understanding tasks in a single model, we show these MLLMs exhibit self-contradiction where generation produces images deemed misaligned with input prompts based on the model's own understanding. We define a Nonunified score that quantifies such self-contradiction. Our empirical results reveal that the self-contradiction mainly arises from weak generation that fails to align with prompts, rather than misunderstanding. This capability asymmetry indicates the potential of leveraging self-contradiction for self-improvement, where the stronger model understanding guides the weaker generation to mitigate the generation-understanding gap. Applying standard post-training methods (e.g., SFT, DPO) with such internal supervision successfully improves both generation and unification. We discover a co-improvement effect on both generation and understanding when only fine-tuning the generation branch, a phenomenon known in pre-training but underexplored in post-training. Our analysis shows improvements stem from better detection of false positives that are previously incorrectly identified as prompt-aligned. Theoretically, we show the aligned training dynamics between generation and understanding allow reduced prompt-misaligned generations to also improve mismatch detection in the understanding branch. Additionally, the framework reveals a potential risk of co-degradation under poor supervision-an overlooked phenomenon that is empirically validated in our experiments. Notably, we find intrinsic metrics like Nonunified score cannot distinguish co-degradation from co-improvement, which highlights the necessity of data quality check. Finally, we propose a curriculum-based strategy based on our findings that gradually introduces harder samples as the model improves, leading to better unification and improved MLLM generation and understanding.

On the Mechanism of Reasoning Pattern Selection in Reinforcement Learning for Language Models

Reinforcement learning (RL) has demonstrated remarkable success in enhancing model capabilities, including instruction-following, preference learning, and reasoning. Yet despite its empirical successes, the mechanisms by which RL improves reasoning abilities remain poorly understood. We present a systematic study of Reinforcement Learning with Verifiable Rewards (RLVR), showing that its primary benefit comes from optimizing the selection of existing reasoning patterns. Through extensive experiments, we demonstrate that RLVR-trained models preferentially adopt high-success-rate reasoning patterns while mostly maintaining stable performance on individual patterns. We further develop theoretical analyses on the convergence and training dynamics of RLVR based on a simplified question-reason-answer model. We study the gradient flow and show that RLVR can indeed find the solution that selects the reason pattern with the highest success rate. Besides, our theoretical results reveal two distinct regimes regarding the convergence of RLVR training: (1) rapid convergence for models with relatively strong initial reasoning capabilities versus (2) slower optimization dynamics for weaker models. Furthermore, we show that the slower optimization for weaker models can be mitigated by applying the supervised fine-tuning (SFT) before RLVR, when using a feasibly high-quality SFT dataset. We validate the theoretical findings through extensive experiments. This work advances our theoretical understanding of RL's role in LLM fine-tuning and offers insights for further enhancing reasoning capabilities.

Model Unlearning via Sparse Autoencoder Subspace Guided Projections

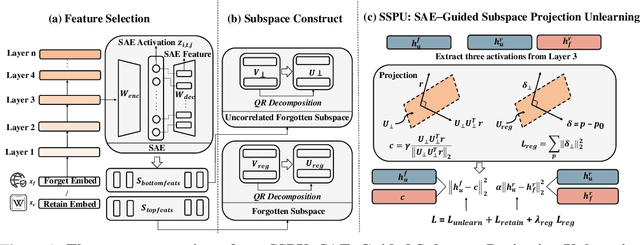
Large language models (LLMs) store vast amounts of information, making them powerful yet raising privacy and safety concerns when selective knowledge removal is required. Existing unlearning strategies, ranging from gradient-based fine-tuning and model editing to sparse autoencoder (SAE) steering, either lack interpretability or fail to provide a robust defense against adversarial prompts. We propose SAE-Guided Subspace Projection Unlearning (SSPU), a novel framework that leverages SAE features to drive targeted updates in the model's parameter space, enabling precise, interpretable, and robust unlearning. SSPU's three-stage pipeline performs data-driven layer and feature selection, subspace construction via QR decomposition, and constrained optimization that controls activations into an "irrelevant" subspace while preserving retained knowledge. Overall, we use SAE features to construct a subspace that supervises unlearning, refining the loss and adding a regularization term to guide interpretable parameter updates. In experiments on the WMDP-Cyber forget set and three utility benchmarks (MMLU, TruthfulQA, GSM8K), SSPU reduces harmful knowledge accuracy by 3.22% compared to the strongest baseline. It also improves adversarial robustness, lowering malicious accuracy under jailbreak prompts compared to baselines. Our findings expose the limitations of prior unlearning methods and demonstrate how interpretable subspace-guided optimization can achieve robust, controllable model behavior.

Physics-Informed Distillation of Diffusion Models for PDE-Constrained Generation

Modeling physical systems in a generative manner offers several advantages, including the ability to handle partial observations, generate diverse solutions, and address both forward and inverse problems. Recently, diffusion models have gained increasing attention in the modeling of physical systems, particularly those governed by partial differential equations (PDEs). However, diffusion models only access noisy data $\boldsymbol{x}_t$ at intermediate steps, making it infeasible to directly enforce constraints on the clean sample $\boldsymbol{x}_0$ at each noisy level. As a workaround, constraints are typically applied to the expectation of clean samples $\mathbb{E}[\boldsymbol{x}_0|\boldsymbol{x}_t]$, which is estimated using the learned score network. However, imposing PDE constraints on the expectation does not strictly represent the one on the true clean data, known as Jensen's Gap. This gap creates a trade-off: enforcing PDE constraints may come at the cost of reduced accuracy in generative modeling. To address this, we propose a simple yet effective post-hoc distillation approach, where PDE constraints are not injected directly into the diffusion process, but instead enforced during a post-hoc distillation stage. We term our method as Physics-Informed Distillation of Diffusion Models (PIDDM). This distillation not only facilitates single-step generation with improved PDE satisfaction, but also support both forward and inverse problem solving and reconstruction from randomly partial observation. Extensive experiments across various PDE benchmarks demonstrate that PIDDM significantly improves PDE satisfaction over several recent and competitive baselines, such as PIDM, DiffusionPDE, and ECI-sampling, with less computation overhead. Our approach can shed light on more efficient and effective strategies for incorporating physical constraints into diffusion models.

Almost Linear Convergence under Minimal Score Assumptions: Quantized Transition Diffusion

Continuous diffusion models have demonstrated remarkable performance in data generation across various domains, yet their efficiency remains constrained by two critical limitations: (1) the local adjacency structure of the forward Markov process, which restricts long-range transitions in the data space, and (2) inherent biases introduced during the simulation of time-inhomogeneous reverse denoising processes. To address these challenges, we propose Quantized Transition Diffusion (QTD), a novel approach that integrates data quantization with discrete diffusion dynamics. Our method first transforms the continuous data distribution $p_*$ into a discrete one $q_*$ via histogram approximation and binary encoding, enabling efficient representation in a structured discrete latent space. We then design a continuous-time Markov chain (CTMC) with Hamming distance-based transitions as the forward process, which inherently supports long-range movements in the original data space. For reverse-time sampling, we introduce a \textit{truncated uniformization} technique to simulate the reverse CTMC, which can provably provide unbiased generation from $q_*$ under minimal score assumptions. Through a novel KL dynamic analysis of the reverse CTMC, we prove that QTD can generate samples with $O(d\ln^2(d/\epsilon))$ score evaluations in expectation to approximate the $d$--dimensional target distribution $p_*$ within an $\epsilon$ error tolerance. Our method not only establishes state-of-the-art inference efficiency but also advances the theoretical foundations of diffusion-based generative modeling by unifying discrete and continuous diffusion paradigms.

Capturing Conditional Dependence via Auto-regressive Diffusion Models

Diffusion models have demonstrated appealing performance in both image and video generation. However, many works discover that they struggle to capture important, high-level relationships that are present in the real world. For example, they fail to learn physical laws from data, and even fail to understand that the objects in the world exist in a stable fashion. This is due to the fact that important conditional dependence structures are not adequately captured in the vanilla diffusion models. In this work, we initiate an in-depth study on strengthening the diffusion model to capture the conditional dependence structures in the data. In particular, we examine the efficacy of the auto-regressive (AR) diffusion models for such purpose and develop the first theoretical results on the sampling error of AR diffusion models under (possibly) the mildest data assumption. Our theoretical findings indicate that, compared with typical diffusion models, the AR variant produces samples with a reduced gap in approximating the data conditional distribution. On the other hand, the overall inference time of the AR-diffusion models is only moderately larger than that for the vanilla diffusion models, making them still practical for large scale applications. We also provide empirical results showing that when there is clear conditional dependence structure in the data, the AR diffusion models captures such structure, whereas vanilla DDPM fails to do so. On the other hand, when there is no obvious conditional dependence across patches of the data, AR diffusion does not outperform DDPM.

Gradient Descent Robustly Learns the Intrinsic Dimension of Data in Training Convolutional Neural Networks

Modern neural networks are usually highly over-parameterized. Behind the wide usage of over-parameterized networks is the belief that, if the data are simple, then the trained network will be automatically equivalent to a simple predictor. Following this intuition, many existing works have studied different notions of "ranks" of neural networks and their relation to the rank of data. In this work, we study the rank of convolutional neural networks (CNNs) trained by gradient descent, with a specific focus on the robustness of the rank to image background noises. Specifically, we point out that, when adding background noises to images, the rank of the CNN trained with gradient descent is affected far less compared with the rank of the data. We support our claim with a theoretical case study, where we consider a particular data model to characterize low-rank clean images with added background noises. We prove that CNNs trained by gradient descent can learn the intrinsic dimension of clean images, despite the presence of relatively large background noises. We also conduct experiments on synthetic and real datasets to further validate our claim.

STGAN: Spatial-temporal Graph Autoregression Network for Pavement Distress Deterioration Prediction

Pavement distress significantly compromises road integrity and poses risks to drivers. Accurate prediction of pavement distress deterioration is essential for effective road management, cost reduction in maintenance, and improvement of traffic safety. However, real-world data on pavement distress is usually collected irregularly, resulting in uneven, asynchronous, and sparse spatial-temporal datasets. This hinders the application of existing spatial-temporal models, such as DCRNN, since they are only applicable to regularly and synchronously collected data. To overcome these challenges, we propose the Spatial-Temporal Graph Autoregression Network (STGAN), a novel graph neural network model designed for accurately predicting irregular pavement distress deterioration using complex spatial-temporal data. Specifically, STGAN integrates the temporal domain into the spatial domain, creating a larger graph where nodes are represented by spatial-temporal tuples and edges are formed based on a similarity-based connection mechanism. Furthermore, based on the constructed spatiotemporal graph, we formulate pavement distress deterioration prediction as a graph autoregression task, i.e., the graph size increases incrementally and the prediction is performed sequentially. This is accomplished by a novel spatial-temporal attention mechanism deployed by STGAN. Utilizing the ConTrack dataset, which contains pavement distress records collected from different locations in Shanghai, we demonstrate the superior performance of STGAN in capturing spatial-temporal correlations and addressing the aforementioned challenges. Experimental results further show that STGAN outperforms baseline models, and ablation studies confirm the effectiveness of its novel modules. Our findings contribute to promoting proactive road maintenance decision-making and ultimately enhancing road safety and resilience.