MathCanvas: Intrinsic Visual Chain-of-Thought for Multimodal Mathematical Reasoning

While Large Language Models (LLMs) have excelled in textual reasoning, they struggle with mathematical domains like geometry that intrinsically rely on visual aids. Existing approaches to Visual Chain-of-Thought (VCoT) are often limited by rigid external tools or fail to generate the high-fidelity, strategically-timed diagrams necessary for complex problem-solving. To bridge this gap, we introduce MathCanvas, a comprehensive framework designed to endow unified Large Multimodal Models (LMMs) with intrinsic VCoT capabilities for mathematics. Our approach consists of two phases. First, a Visual Manipulation stage pre-trains the model on a novel 15.2M-pair corpus, comprising 10M caption-to-diagram pairs (MathCanvas-Imagen) and 5.2M step-by-step editing trajectories (MathCanvas-Edit), to master diagram generation and editing. Second, a Strategic Visual-Aided Reasoning stage fine-tunes the model on MathCanvas-Instruct, a new 219K-example dataset of interleaved visual-textual reasoning paths, teaching it when and how to leverage visual aids. To facilitate rigorous evaluation, we introduce MathCanvas-Bench, a challenging benchmark with 3K problems that require models to produce interleaved visual-textual solutions. Our model, BAGEL-Canvas, trained under this framework, achieves an 86% relative improvement over strong LMM baselines on MathCanvas-Bench, demonstrating excellent generalization to other public math benchmarks. Our work provides a complete toolkit-framework, datasets, and benchmark-to unlock complex, human-like visual-aided reasoning in LMMs. Project Page: https://mathcanvas.github.io/

VoiceAssistant-Eval: Benchmarking AI Assistants across Listening, Speaking, and Viewing

The growing capabilities of large language models and multimodal systems have spurred interest in voice-first AI assistants, yet existing benchmarks are inadequate for evaluating the full range of these systems' capabilities. We introduce VoiceAssistant-Eval, a comprehensive benchmark designed to assess AI assistants across listening, speaking, and viewing. VoiceAssistant-Eval comprises 10,497 curated examples spanning 13 task categories. These tasks include natural sounds, music, and spoken dialogue for listening; multi-turn dialogue, role-play imitation, and various scenarios for speaking; and highly heterogeneous images for viewing. To demonstrate its utility, we evaluate 21 open-source models and GPT-4o-Audio, measuring the quality of the response content and speech, as well as their consistency. The results reveal three key findings: (1) proprietary models do not universally outperform open-source models; (2) most models excel at speaking tasks but lag in audio understanding; and (3) well-designed smaller models can rival much larger ones. Notably, the mid-sized Step-Audio-2-mini (7B) achieves more than double the listening accuracy of LLaMA-Omni2-32B-Bilingual. However, challenges remain: multimodal (audio plus visual) input and role-play voice imitation tasks are difficult for current models, and significant gaps persist in robustness and safety alignment. VoiceAssistant-Eval identifies these gaps and establishes a rigorous framework for evaluating and guiding the development of next-generation AI assistants. Code and data will be released at https://mathllm.github.io/VoiceAssistantEval/ .

WebGen-Agent: Enhancing Interactive Website Generation with Multi-Level Feedback and Step-Level Reinforcement Learning

Agent systems powered by large language models (LLMs) have demonstrated impressive performance on repository-level code-generation tasks. However, for tasks such as website codebase generation, which depend heavily on visual effects and user-interaction feedback, current code agents rely only on simple code execution for feedback and verification. This approach fails to capture the actual quality of the generated code. In this paper, we propose WebGen-Agent, a novel website-generation agent that leverages comprehensive and multi-level visual feedback to iteratively generate and refine the website codebase. Detailed and expressive text descriptions and suggestions regarding the screenshots and GUI-agent testing of the websites are generated by a visual language model (VLM), together with scores that quantify their quality. The screenshot and GUI-agent scores are further integrated with a backtracking and select-best mechanism, enhancing the performance of the agent. Utilizing the accurate visual scores inherent in the WebGen-Agent workflow, we further introduce \textit{Step-GRPO with Screenshot and GUI-agent Feedback} to improve the ability of LLMs to act as the reasoning engine of WebGen-Agent. By using the screenshot and GUI-agent scores at each step as the reward in Step-GRPO, we provide a dense and reliable process supervision signal, which effectively improves the model's website-generation ability. On the WebGen-Bench dataset, WebGen-Agent increases the accuracy of Claude-3.5-Sonnet from 26.4% to 51.9% and its appearance score from 3.0 to 3.9, outperforming the previous state-of-the-art agent system. Additionally, our Step-GRPO training approach increases the accuracy of Qwen2.5-Coder-7B-Instruct from 38.9% to 45.4% and raises the appearance score from 3.4 to 3.7.

Alignment with Fill-In-the-Middle for Enhancing Code Generation

The code generation capabilities of Large Language Models (LLMs) have advanced applications like tool invocation and problem-solving. However, improving performance in code-related tasks remains challenging due to limited training data that is verifiable with accurate test cases. While Direct Preference Optimization (DPO) has shown promise, existing methods for generating test cases still face limitations. In this paper, we propose a novel approach that splits code snippets into smaller, granular blocks, creating more diverse DPO pairs from the same test cases. Additionally, we introduce the Abstract Syntax Tree (AST) splitting and curriculum training method to enhance the DPO training. Our approach demonstrates significant improvements in code generation tasks, as validated by experiments on benchmark datasets such as HumanEval (+), MBPP (+), APPS, LiveCodeBench, and BigCodeBench. Code and data are available at https://github.com/SenseLLM/StructureCoder.

Probability-Consistent Preference Optimization for Enhanced LLM Reasoning

Recent advances in preference optimization have demonstrated significant potential for improving mathematical reasoning capabilities in large language models (LLMs). While current approaches leverage high-quality pairwise preference data through outcome-based criteria like answer correctness or consistency, they fundamentally neglect the internal logical coherence of responses. To overcome this, we propose Probability-Consistent Preference Optimization (PCPO), a novel framework that establishes dual quantitative metrics for preference selection: (1) surface-level answer correctness and (2) intrinsic token-level probability consistency across responses. Extensive experiments show that our PCPO consistently outperforms existing outcome-only criterion approaches across a diverse range of LLMs and benchmarks. Our code is publicly available at https://github.com/YunqiaoYang/PCPO.

UI-Genie: A Self-Improving Approach for Iteratively Boosting MLLM-based Mobile GUI Agents

In this paper, we introduce UI-Genie, a self-improving framework addressing two key challenges in GUI agents: verification of trajectory outcome is challenging and high-quality training data are not scalable. These challenges are addressed by a reward model and a self-improving pipeline, respectively. The reward model, UI-Genie-RM, features an image-text interleaved architecture that efficiently pro- cesses historical context and unifies action-level and task-level rewards. To sup- port the training of UI-Genie-RM, we develop deliberately-designed data genera- tion strategies including rule-based verification, controlled trajectory corruption, and hard negative mining. To address the second challenge, a self-improvement pipeline progressively expands solvable complex GUI tasks by enhancing both the agent and reward models through reward-guided exploration and outcome verification in dynamic environments. For training the model, we generate UI- Genie-RM-517k and UI-Genie-Agent-16k, establishing the first reward-specific dataset for GUI agents while demonstrating high-quality synthetic trajectory gen- eration without manual annotation. Experimental results show that UI-Genie achieves state-of-the-art performance across multiple GUI agent benchmarks with three generations of data-model self-improvement. We open-source our complete framework implementation and generated datasets to facilitate further research in https://github.com/Euphoria16/UI-Genie.

MathCoder-VL: Bridging Vision and Code for Enhanced Multimodal Mathematical Reasoning

Natural language image-caption datasets, widely used for training Large Multimodal Models, mainly focus on natural scenarios and overlook the intricate details of mathematical figures that are critical for problem-solving, hindering the advancement of current LMMs in multimodal mathematical reasoning. To this end, we propose leveraging code as supervision for cross-modal alignment, since code inherently encodes all information needed to generate corresponding figures, establishing a precise connection between the two modalities. Specifically, we co-develop our image-to-code model and dataset with model-in-the-loop approach, resulting in an image-to-code model, FigCodifier and ImgCode-8.6M dataset, the largest image-code dataset to date. Furthermore, we utilize FigCodifier to synthesize novel mathematical figures and then construct MM-MathInstruct-3M, a high-quality multimodal math instruction fine-tuning dataset. Finally, we present MathCoder-VL, trained with ImgCode-8.6M for cross-modal alignment and subsequently fine-tuned on MM-MathInstruct-3M for multimodal math problem solving. Our model achieves a new open-source SOTA across all six metrics. Notably, it surpasses GPT-4o and Claude 3.5 Sonnet in the geometry problem-solving subset of MathVista, achieving improvements of 8.9% and 9.2%. The dataset and models will be released at https://github.com/mathllm/MathCoder.

WebGen-Bench: Evaluating LLMs on Generating Interactive and Functional Websites from Scratch

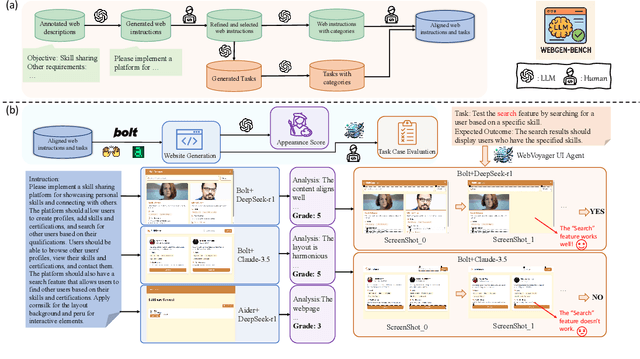
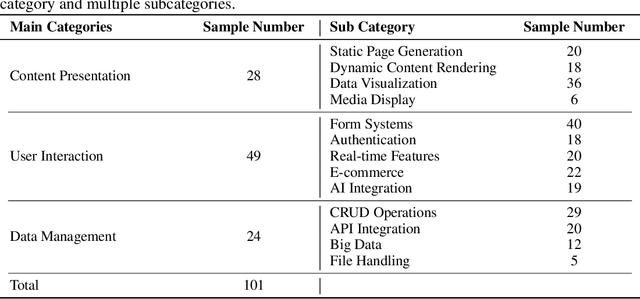
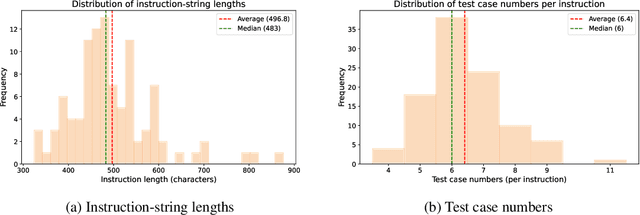
LLM-based agents have demonstrated great potential in generating and managing code within complex codebases. In this paper, we introduce WebGen-Bench, a novel benchmark designed to measure an LLM-based agent's ability to create multi-file website codebases from scratch. It contains diverse instructions for website generation, created through the combined efforts of human annotators and GPT-4o. These instructions span three major categories and thirteen minor categories, encompassing nearly all important types of web applications. To assess the quality of the generated websites, we use GPT-4o to generate test cases targeting each functionality described in the instructions, and then manually filter, adjust, and organize them to ensure accuracy, resulting in 647 test cases. Each test case specifies an operation to be performed on the website and the expected result after the operation. To automate testing and improve reproducibility, we employ a powerful web-navigation agent to execute tests on the generated websites and determine whether the observed responses align with the expected results. We evaluate three high-performance code-agent frameworks, Bolt.diy, OpenHands, and Aider, using multiple proprietary and open-source LLMs as engines. The best-performing combination, Bolt.diy powered by DeepSeek-R1, achieves only 27.8\% accuracy on the test cases, highlighting the challenging nature of our benchmark. Additionally, we construct WebGen-Instruct, a training set consisting of 6,667 website-generation instructions. Training Qwen2.5-Coder-32B-Instruct on Bolt.diy trajectories generated from a subset of this training set achieves an accuracy of 38.2\%, surpassing the performance of the best proprietary model.

MathCoder2: Better Math Reasoning from Continued Pretraining on Model-translated Mathematical Code

Code has been shown to be effective in enhancing the mathematical reasoning abilities of large language models due to its precision and accuracy. Previous works involving continued mathematical pretraining often include code that utilizes math-related packages, which are primarily designed for fields such as engineering, machine learning, signal processing, or module testing, rather than being directly focused on mathematical reasoning. In this paper, we introduce a novel method for generating mathematical code accompanied with corresponding reasoning steps for continued pretraining. Our approach begins with the construction of a high-quality mathematical continued pretraining dataset by incorporating math-related web data, code using mathematical packages, math textbooks, and synthetic data. Next, we construct reasoning steps by extracting LaTeX expressions, the conditions needed for the expressions, and the results of the expressions from the previously collected dataset. Based on this extracted information, we generate corresponding code to accurately capture the mathematical reasoning process. Appending the generated code to each reasoning step results in data consisting of paired natural language reasoning steps and their corresponding code. Combining this data with the original dataset results in a 19.2B-token high-performing mathematical pretraining corpus, which we name MathCode-Pile. Training several popular base models with this corpus significantly improves their mathematical abilities, leading to the creation of the MathCoder2 family of models. All of our data processing and training code is open-sourced, ensuring full transparency and easy reproducibility of the entire data collection and training pipeline. The code is released at https://github.com/mathllm/MathCoder2 .

Step-Controlled DPO: Leveraging Stepwise Error for Enhanced Mathematical Reasoning

Direct Preference Optimization (DPO) has proven effective at improving the performance of large language models (LLMs) on downstream tasks such as reasoning and alignment. In this work, we propose Step-Controlled DPO (SCDPO), a method for automatically providing stepwise error supervision by creating negative samples of mathematical reasoning rationales that start making errors at a specified step. By applying these samples in DPO training, SCDPO can better align the model to understand reasoning errors and output accurate reasoning steps. We apply SCDPO to both code-integrated and chain-of-thought solutions, empirically showing that it consistently improves the performance compared to naive DPO on three different SFT models, including one existing SFT model and two models we finetuned. Qualitative analysis of the credit assignment of SCDPO and DPO demonstrates the effectiveness of SCDPO at identifying errors in mathematical solutions. We then apply SCDPO to an InternLM2-20B model, resulting in a 20B model that achieves high scores of 88.5% on GSM8K and 58.1% on MATH, rivaling all other open-source LLMs, showing the great potential of our method.