Xiaolin Huang
Subspace Adversarial Training
Nov 24, 2021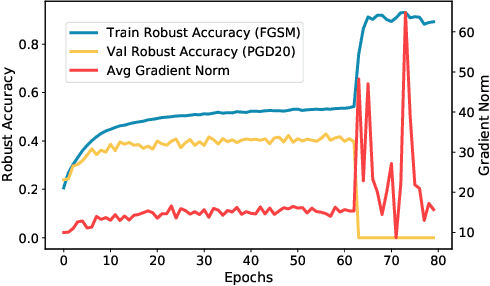
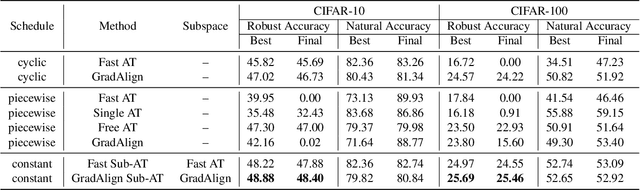
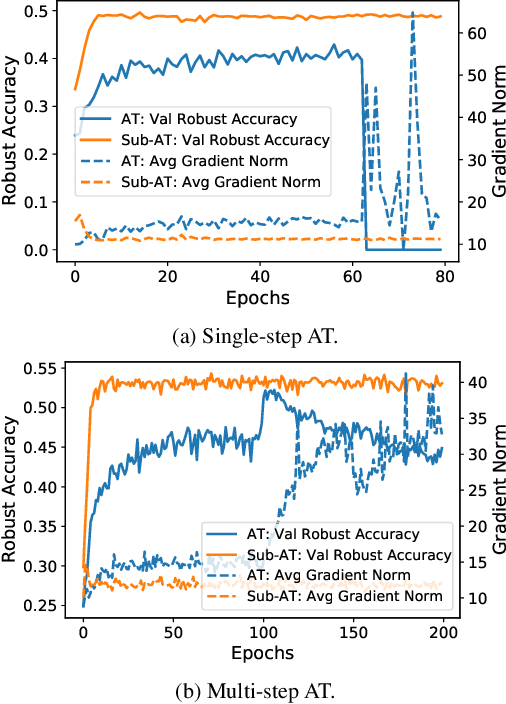
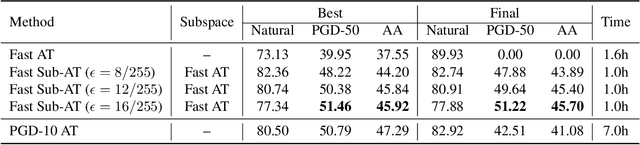
Abstract:Single-step adversarial training (AT) has received wide attention as it proved to be both efficient and robust. However, a serious problem of catastrophic overfitting exists, i.e., the robust accuracy against projected gradient descent (PGD) attack suddenly drops to $0\%$ during the training. In this paper, we understand this problem from a novel perspective of optimization and firstly reveal the close link between the fast-growing gradient of each sample and overfitting, which can also be applied to understand the robust overfitting phenomenon in multi-step AT. To control the growth of the gradient during the training, we propose a new AT method, subspace adversarial training (Sub-AT), which constrains the AT in a carefully extracted subspace. It successfully resolves both two kinds of overfitting and hence significantly boosts the robustness. In subspace, we also allow single-step AT with larger steps and larger radius, which further improves the robustness performance. As a result, we achieve the state-of-the-art single-step AT performance: our pure single-step AT can reach over $\mathbf{51}\%$ robust accuracy against strong PGD-50 attack with radius $8/255$ on CIFAR-10, even surpassing the standard multi-step PGD-10 AT with huge computational advantages. The code is released$\footnote{\url{https://github.com/nblt/Sub-AT}}$.
Semi-tensor Product-based TensorDecomposition for Neural Network Compression
Sep 30, 2021
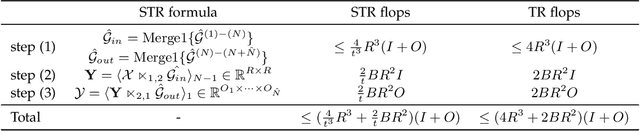
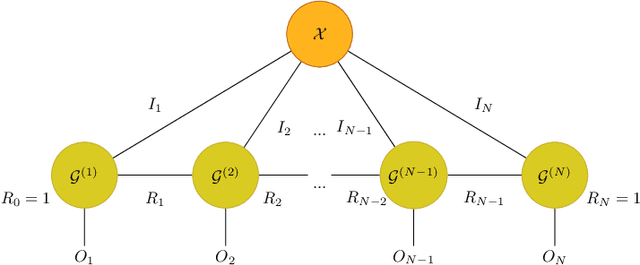

Abstract:The existing tensor networks adopt conventional matrix product for connection. The classical matrix product requires strict dimensionality consistency between factors, which can result in redundancy in data representation. In this paper, the semi-tensor product is used to generalize classical matrix product-based mode product to semi-tensor mode product. As it permits the connection of two factors with different dimensionality, more flexible and compact tensor decompositions can be obtained with smaller sizes of factors. Tucker decomposition, Tensor Train (TT) and Tensor Ring (TR) are common decomposition for low rank compression of deep neural networks. The semi-tensor product is applied to these tensor decompositions to obtained their generalized versions, i.e., semi-tensor Tucker decomposition (STTu), semi-tensor train(STT) and semi-tensor ring (STR). Experimental results show the STTu, STT and STR achieve higher compression factors than the conventional tensor decompositions with the same accuracy but less training times in ResNet and WideResNetcompression. With 2% accuracy degradation, the TT-RN (rank = 14) and the TR-WRN (rank = 16) only obtain 3 times and99t times compression factors while the STT-RN (rank = 14) and the STR-WRN (rank = 16) achieve 9 times and 179 times compression factors, respectively.
A Generalized Framework for Edge-preserving and Structure-preserving Image Smoothing
Aug 04, 2021
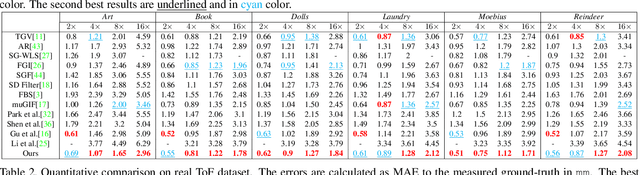
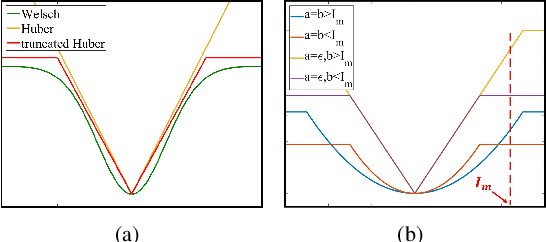

Abstract:Image smoothing is a fundamental procedure in applications of both computer vision and graphics. The required smoothing properties can be different or even contradictive among different tasks. Nevertheless, the inherent smoothing nature of one smoothing operator is usually fixed and thus cannot meet the various requirements of different applications. In this paper, we first introduce the truncated Huber penalty function which shows strong flexibility under different parameter settings. A generalized framework is then proposed with the introduced truncated Huber penalty function. When combined with its strong flexibility, our framework is able to achieve diverse smoothing natures where contradictive smoothing behaviors can even be achieved. It can also yield the smoothing behavior that can seldom be achieved by previous methods, and superior performance is thus achieved in challenging cases. These together enable our framework capable of a range of applications and able to outperform the state-of-the-art approaches in several tasks, such as image detail enhancement, clip-art compression artifacts removal, guided depth map restoration, image texture removal, etc. In addition, an efficient numerical solution is provided and its convergence is theoretically guaranteed even the optimization framework is non-convex and non-smooth. A simple yet effective approach is further proposed to reduce the computational cost of our method while maintaining its performance. The effectiveness and superior performance of our approach are validated through comprehensive experiments in a range of applications. Our code is available at https://github.com/wliusjtu/Generalized-Smoothing-Framework.
Adaptive Feature Alignment for Adversarial Training
Jun 16, 2021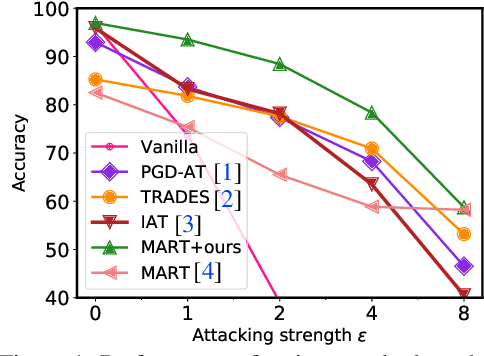
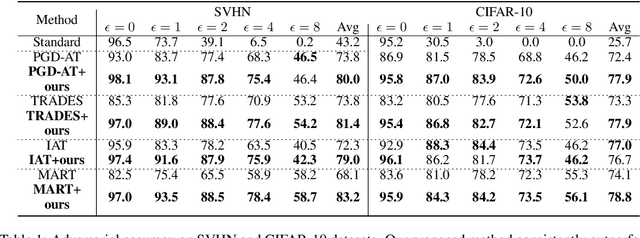
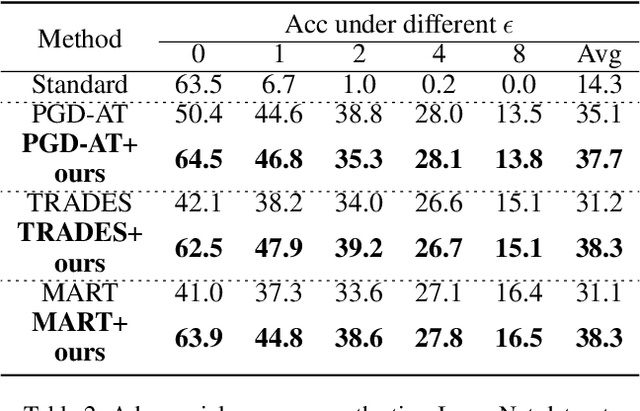
Abstract:Recent studies reveal that Convolutional Neural Networks (CNNs) are typically vulnerable to adversarial attacks, which pose a threat to security-sensitive applications. Many adversarial defense methods improve robustness at the cost of accuracy, raising the contradiction between standard and adversarial accuracies. In this paper, we observe an interesting phenomenon that feature statistics change monotonically and smoothly w.r.t the rising of attacking strength. Based on this observation, we propose the adaptive feature alignment (AFA) to generate features of arbitrary attacking strengths. Our method is trained to automatically align features of arbitrary attacking strength. This is done by predicting a fusing weight in a dual-BN architecture. Unlike previous works that need to either retrain the model or manually tune a hyper-parameters for different attacking strengths, our method can deal with arbitrary attacking strengths with a single model without introducing any hyper-parameter. Importantly, our method improves the model robustness against adversarial samples without incurring much loss in standard accuracy. Experiments on CIFAR-10, SVHN, and tiny-ImageNet datasets demonstrate that our method outperforms the state-of-the-art under a wide range of attacking strengths.
Dominant Patterns: Critical Features Hidden in Deep Neural Networks
May 31, 2021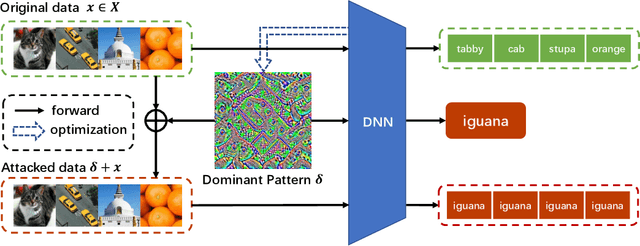
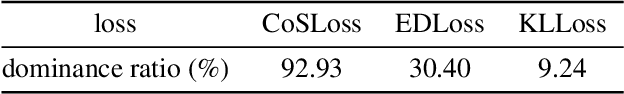

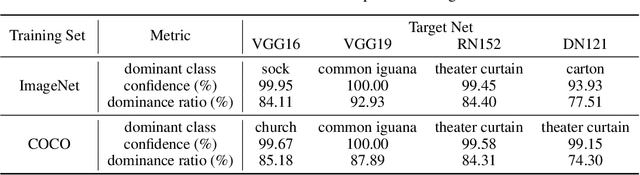
Abstract:In this paper, we find the existence of critical features hidden in Deep NeuralNetworks (DNNs), which are imperceptible but can actually dominate the outputof DNNs. We call these features dominant patterns. As the name suggests, for a natural image, if we add the dominant pattern of a DNN to it, the output of this DNN is determined by the dominant pattern instead of the original image, i.e., DNN's prediction is the same with the dominant pattern's. We design an algorithm to find such patterns by pursuing the insensitivity in the feature space. A direct application of the dominant patterns is the Universal Adversarial Perturbations(UAPs). Numerical experiments show that the found dominant patterns defeat state-of-the-art UAP methods, especially in label-free settings. In addition, dominant patterns are proved to have the potential to attack downstream tasks in which DNNs share the same backbone. We claim that DNN-specific dominant patterns reveal some essential properties of a DNN and are of great importance for its feature analysis and robustness enhancement.
QueryNet: An Efficient Attack Framework with Surrogates Carrying Multiple Identities
May 31, 2021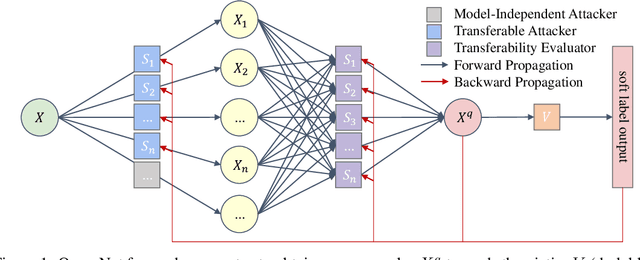
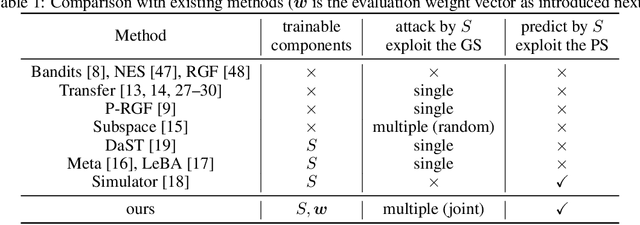

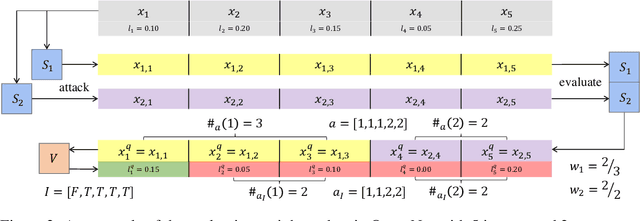
Abstract:Deep Neural Networks (DNNs) are acknowledged as vulnerable to adversarial attacks, while the existing black-box attacks require extensive queries on the victim DNN to achieve high success rates. For query-efficiency, surrogate models of the victim are adopted as transferable attackers in consideration of their Gradient Similarity (GS), i.e., surrogates' attack gradients are similar to the victim's ones to some extent. However, it is generally neglected to exploit their similarity on outputs, namely the Prediction Similarity (PS), to filter out inefficient queries. To jointly utilize and also optimize surrogates' GS and PS, we develop QueryNet, an efficient attack network that can significantly reduce queries. QueryNet crafts several transferable Adversarial Examples (AEs) by surrogates, and then decides also by surrogates on the most promising AE, which is then sent to query the victim. That is to say, in QueryNet, surrogates are not only exploited as transferable attackers, but also as transferability evaluators for AEs. The AEs are generated using surrogates' GS and evaluated based on their FS, and therefore, the query results could be back-propagated to optimize surrogates' parameters and also their architectures, enhancing both the GS and the FS. QueryNet has significant query-efficiency, i.e., reduces queries by averagely about an order of magnitude compared to recent SOTA methods according to our comprehensive and real-world experiments: 11 victims (including 2 commercial models) on MNIST/CIFAR10/ImageNet, allowing only 8-bit image queries, and no access to the victim's training data.
Residual Enhanced Multi-Hypergraph Neural Network
May 02, 2021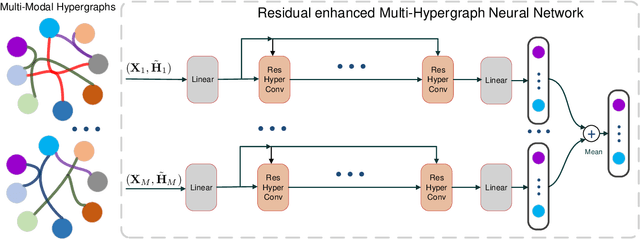

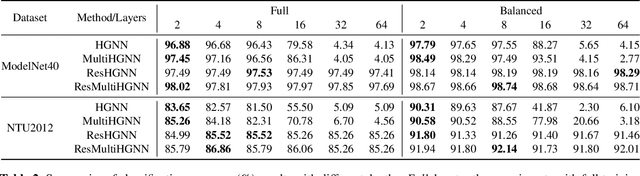
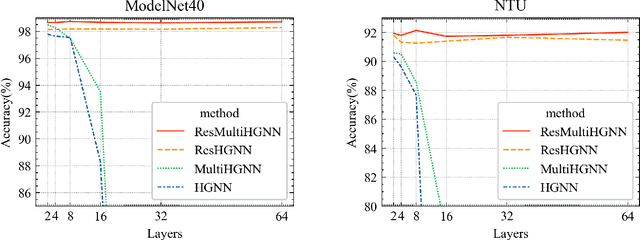
Abstract:Hypergraphs are a generalized data structure of graphs to model higher-order correlations among entities, which have been successfully adopted into various research domains. Meanwhile, HyperGraph Neural Network (HGNN) is currently the de-facto method for hypergraph representation learning. However, HGNN aims at single hypergraph learning and uses a pre-concatenation approach when confronting multi-modal datasets, which leads to sub-optimal exploitation of the inter-correlations of multi-modal hypergraphs. HGNN also suffers the over-smoothing issue, that is, its performance drops significantly when layers are stacked up. To resolve these issues, we propose the Residual enhanced Multi-Hypergraph Neural Network, which can not only fuse multi-modal information from each hypergraph effectively, but also circumvent the over-smoothing issue associated with HGNN. We conduct experiments on two 3D benchmarks, the NTU and the ModelNet40 datasets, and compare against multiple state-of-the-art methods. Experimental results demonstrate that both the residual hypergraph convolutions and the multi-fusion architecture can improve the performance of the base model and the combined model achieves a new state-of-the-art. Code is available at \url{https://github.com/OneForward/ResMHGNN}.
Towards Unbiased Random Features with Lower Variance For Stationary Indefinite Kernels
Apr 14, 2021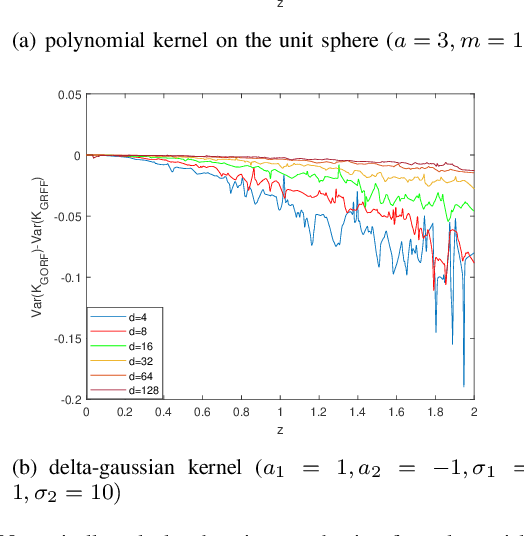
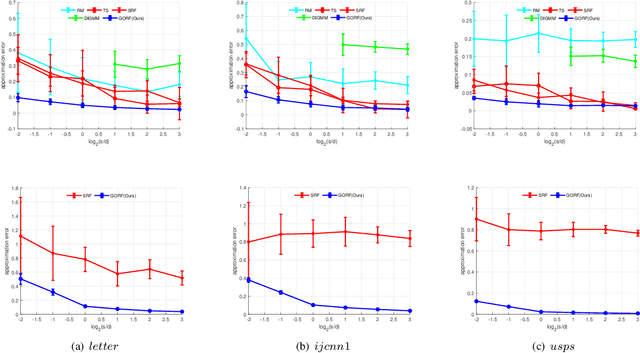
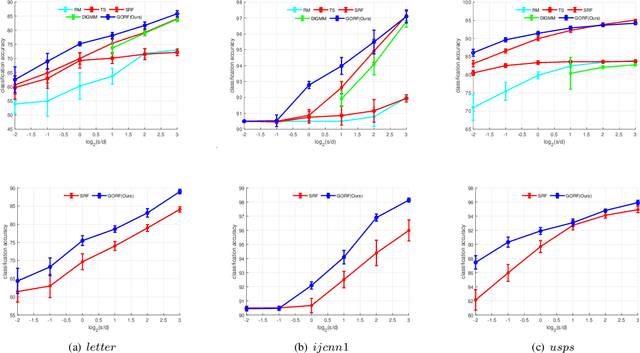
Abstract:Random Fourier Features (RFF) demonstrate wellappreciated performance in kernel approximation for largescale situations but restrict kernels to be stationary and positive definite. And for non-stationary kernels, the corresponding RFF could be converted to that for stationary indefinite kernels when the inputs are restricted to the unit sphere. Numerous methods provide accessible ways to approximate stationary but indefinite kernels. However, they are either biased or possess large variance. In this article, we propose the generalized orthogonal random features, an unbiased estimation with lower variance.Experimental results on various datasets and kernels verify that our algorithm achieves lower variance and approximation error compared with the existing kernel approximation methods. With better approximation to the originally selected kernels, improved classification accuracy and regression ability is obtained with our approximation algorithm in the framework of support vector machine and regression.
Weighted Neural Tangent Kernel: A Generalized and Improved Network-Induced Kernel
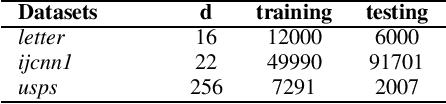
Mar 22, 2021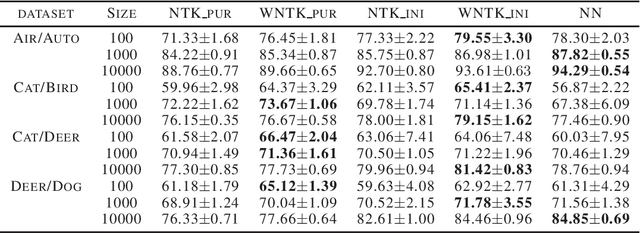
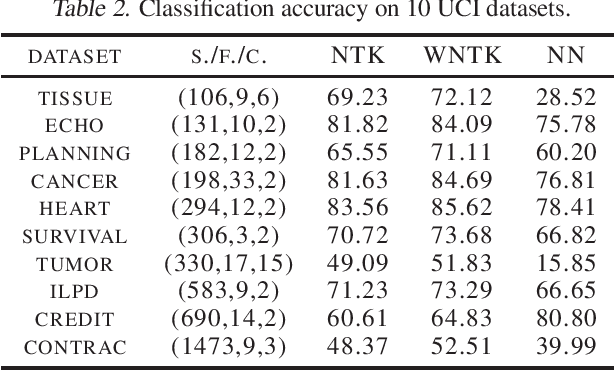
Abstract:The Neural Tangent Kernel (NTK) has recently attracted intense study, as it describes the evolution of an over-parameterized Neural Network (NN) trained by gradient descent. However, it is now well-known that gradient descent is not always a good optimizer for NNs, which can partially explain the unsatisfactory practical performance of the NTK regression estimator. In this paper, we introduce the Weighted Neural Tangent Kernel (WNTK), a generalized and improved tool, which can capture an over-parameterized NN's training dynamics under different optimizers. Theoretically, in the infinite-width limit, we prove: i) the stability of the WNTK at initialization and during training, and ii) the equivalence between the WNTK regression estimator and the corresponding NN estimator with different learning rates on different parameters. With the proposed weight update algorithm, both empirical and analytical WNTKs outperform the corresponding NTKs in numerical experiments.
Train Deep Neural Networks in 40-D Subspaces
Mar 20, 2021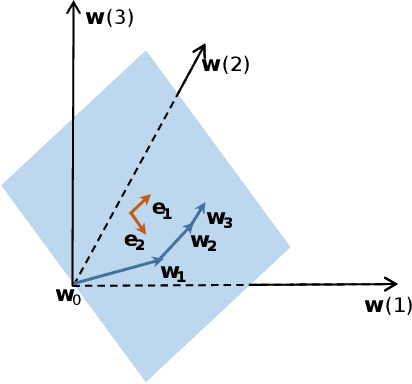
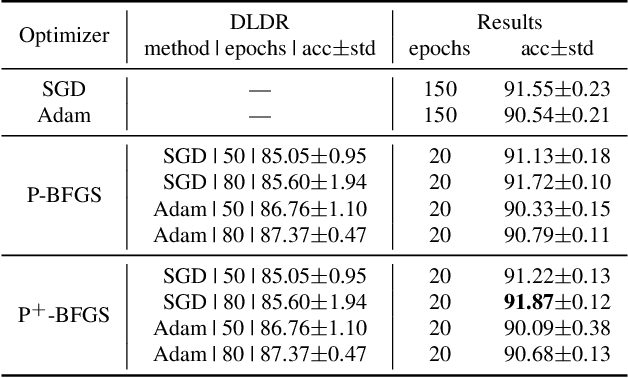
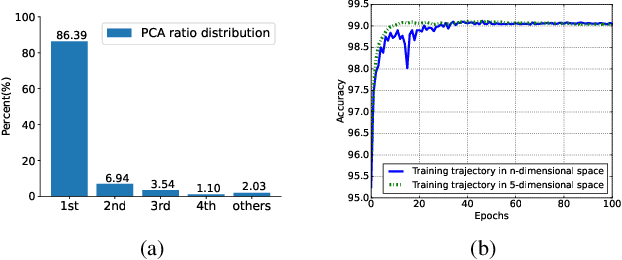
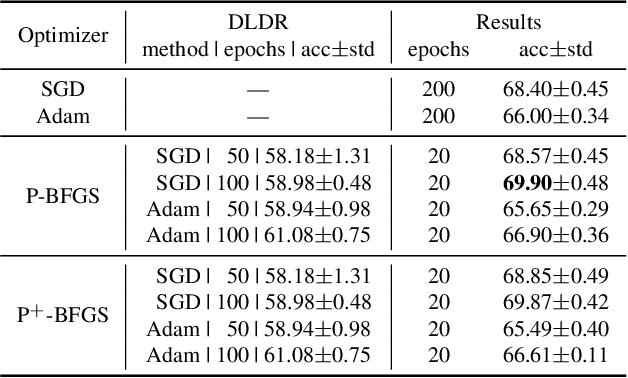
Abstract:Although there are massive parameters in deep neural networks, the training can actually proceed in a rather low-dimensional space. By investigating such low-dimensional properties of the training trajectory, we propose a Dynamic Linear Dimensionality Reduction (DLDR), which dramatically reduces the parameter space to a variable subspace of significantly lower dimension. Since there are only a few variables to optimize, second-order methods become applicable. Following this idea, we develop a quasi-Newton-based algorithm to train these variables obtained by DLDR, rather than the original parameters of neural networks. The experimental results strongly support the dimensionality reduction performance: for many standard neural networks, optimizing over only 40 variables, one can achieve comparable performance against the regular training over thousands or even millions of parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge