DAPE V2: Process Attention Score as Feature Map for Length Extrapolation

The attention mechanism is a fundamental component of the Transformer model, contributing to interactions among distinct tokens, in contrast to earlier feed-forward neural networks. In general, the attention scores are determined simply by the key-query products. However, this work's occasional trial (combining DAPE and NoPE) of including additional MLPs on attention scores without position encoding indicates that the classical key-query multiplication may limit the performance of Transformers. In this work, we conceptualize attention as a feature map and apply the convolution operator (for neighboring attention scores across different heads) to mimic the processing methods in computer vision. Specifically, the main contribution of this paper is identifying and interpreting the Transformer length extrapolation problem as a result of the limited expressiveness of the naive query and key dot product, and we successfully translate the length extrapolation issue into a well-understood feature map processing problem. The novel insight, which can be adapted to various attention-related models, reveals that the current Transformer architecture has the potential for further evolution. Extensive experiments demonstrate that treating attention as a feature map and applying convolution as a processing method significantly enhances Transformer performance.

CAPE: Context-Adaptive Positional Encoding for Length Extrapolation

Positional encoding plays a crucial role in transformers, significantly impacting model performance and length generalization. Prior research has introduced absolute positional encoding (APE) and relative positional encoding (RPE) to distinguish token positions in given sequences. However, both APE and RPE remain fixed after model training regardless of input data, limiting their adaptability and flexibility. Hence, we expect that the desired positional encoding should be context-adaptive and can be dynamically adjusted with the given attention. In this paper, we propose a Context-Adaptive Positional Encoding (CAPE) method, which dynamically and semantically adjusts based on input context and learned fixed priors. Experimental validation on real-world datasets (Arxiv, Books3, and CHE) demonstrates that CAPE enhances model performances in terms of trained length and length generalization, where the improvements are statistically significant. The model visualization suggests that our model can keep both local and anti-local information. Finally, we successfully train the model on sequence length 128 and achieve better performance at evaluation sequence length 8192, compared with other static positional encoding methods, revealing the benefit of the adaptive positional encoding method.

Stability and Generalization of Hypergraph Collaborative Networks

Graph neural networks have been shown to be very effective in utilizing pairwise relationships across samples. Recently, there have been several successful proposals to generalize graph neural networks to hypergraph neural networks to exploit more complex relationships. In particular, the hypergraph collaborative networks yield superior results compared to other hypergraph neural networks for various semi-supervised learning tasks. The collaborative network can provide high quality vertex embeddings and hyperedge embeddings together by formulating them as a joint optimization problem and by using their consistency in reconstructing the given hypergraph. In this paper, we aim to establish the algorithmic stability of the core layer of the collaborative network and provide generalization guarantees. The analysis sheds light on the design of hypergraph filters in collaborative networks, for instance, how the data and hypergraph filters should be scaled to achieve uniform stability of the learning process. Some experimental results on real-world datasets are presented to illustrate the theory.

A Generalized Framework for Edge-preserving and Structure-preserving Image Smoothing

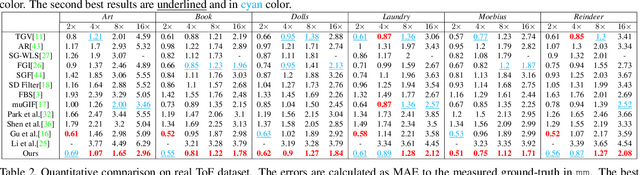
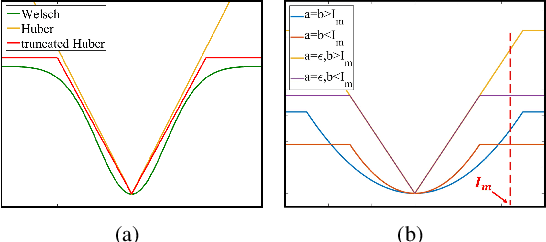
Image smoothing is a fundamental procedure in applications of both computer vision and graphics. The required smoothing properties can be different or even contradictive among different tasks. Nevertheless, the inherent smoothing nature of one smoothing operator is usually fixed and thus cannot meet the various requirements of different applications. In this paper, we first introduce the truncated Huber penalty function which shows strong flexibility under different parameter settings. A generalized framework is then proposed with the introduced truncated Huber penalty function. When combined with its strong flexibility, our framework is able to achieve diverse smoothing natures where contradictive smoothing behaviors can even be achieved. It can also yield the smoothing behavior that can seldom be achieved by previous methods, and superior performance is thus achieved in challenging cases. These together enable our framework capable of a range of applications and able to outperform the state-of-the-art approaches in several tasks, such as image detail enhancement, clip-art compression artifacts removal, guided depth map restoration, image texture removal, etc. In addition, an efficient numerical solution is provided and its convergence is theoretically guaranteed even the optimization framework is non-convex and non-smooth. A simple yet effective approach is further proposed to reduce the computational cost of our method while maintaining its performance. The effectiveness and superior performance of our approach are validated through comprehensive experiments in a range of applications. Our code is available at https://github.com/wliusjtu/Generalized-Smoothing-Framework.

Tucker Decomposition Network: Expressive Power and Comparison

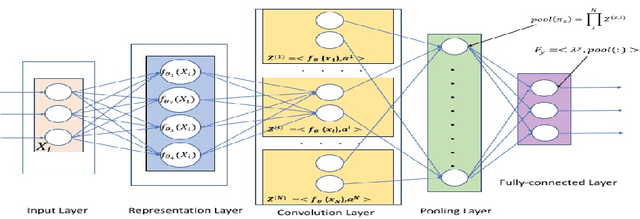
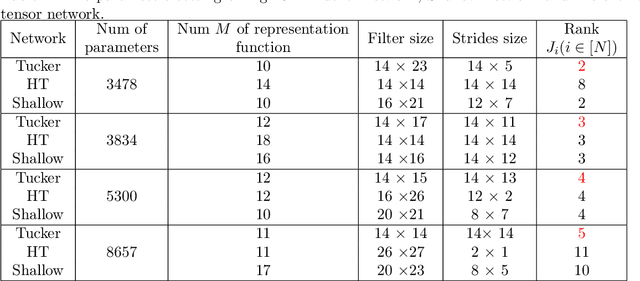
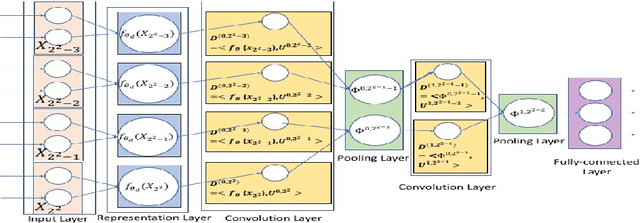
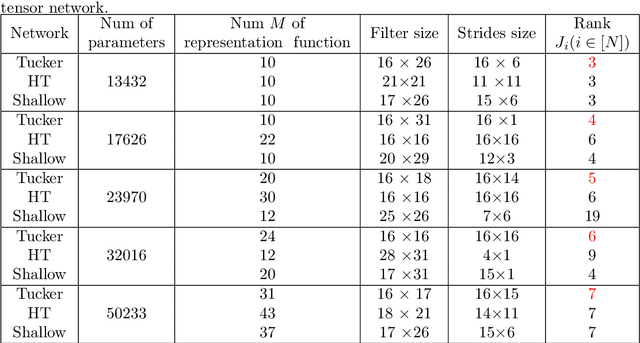
Deep neural networks have achieved a great success in solving many machine learning and computer vision problems. The main contribution of this paper is to develop a deep network based on Tucker tensor decomposition, and analyze its expressive power. It is shown that the expressiveness of Tucker network is more powerful than that of shallow network. In general, it is required to use an exponential number of nodes in a shallow network in order to represent a Tucker network. Experimental results are also given to compare the performance of the proposed Tucker network with hierarchical tensor network and shallow network, and demonstrate the usefulness of Tucker network in image classification problems.

Deep Plug-and-play Prior for Low-rank Tensor Completion

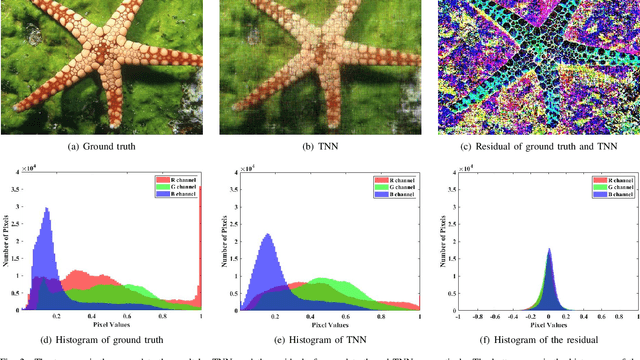
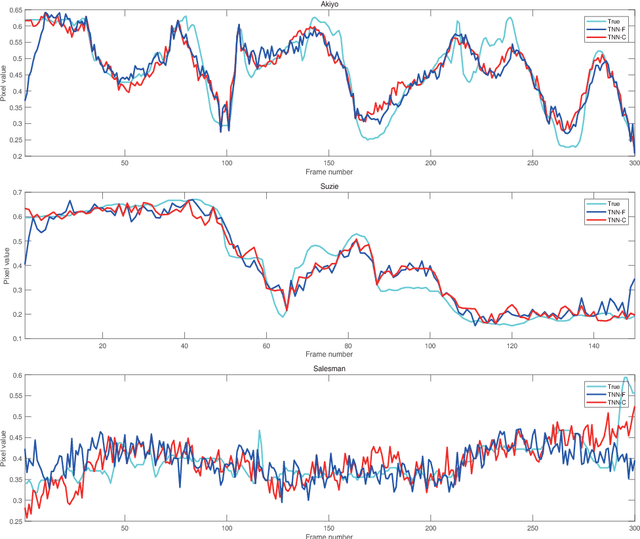
Tensor image data sets such as color images and multispectral images are highly correlated and they contain a lot of image details. The main aim of this paper is to propose and develop a regularized tensor completion model for tensor image data completion. In the objective function, we adopt the newly emerged tensor nuclear norm (TNN) to characterize the global structure of such tensor image data sets. Also, we formulate an implicit regularizer to plug in the convolutional neural network (CNN) denoiser, which is convinced to express the image prior learned from a large amount of natural images. The resulting model can be solved efficiently via an alternating directional method of multipliers algorithm. Experimental results (on color images, videos, and multispectral images) are presented to show that both image global structure and details can be recovered very well, and to illustrate that the performance of the proposed method is better than that of testing methods in terms of PSNR and SSIM.

A Fast Algorithm for Cosine Transform Based Tensor Singular Value Decomposition

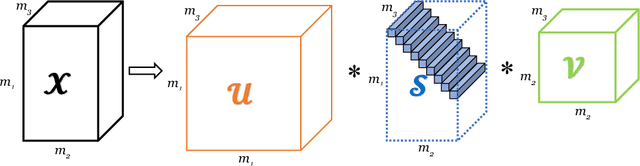
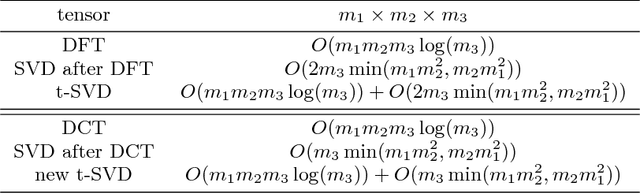
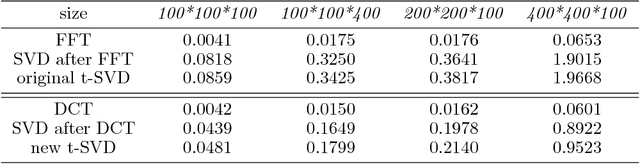
Recently, there has been a lot of research into tensor singular value decomposition (t-SVD) by using discrete Fourier transform (DFT) matrix. The main aims of this paper are to propose and study tensor singular value decomposition based on the discrete cosine transform (DCT) matrix. The advantages of using DCT are that (i) the complex arithmetic is not involved in the cosine transform based tensor singular value decomposition, so the computational cost required can be saved; (ii) the intrinsic reflexive boundary condition along the tubes in the third dimension of tensors is employed, so its performance would be better than that by using the periodic boundary condition in DFT. We demonstrate that the tensor product between two tensors by using DCT can be equivalent to the multiplication between a block Toeplitz-plus-Hankel matrix and a block vector. Numerical examples of low-rank tensor completion are further given to illustrate that the efficiency by using DCT is two times faster than that by using DFT and also the errors of video and multispectral image completion by using DCT are smaller than those by using DFT.

3D Point Cloud Denoising using Graph Laplacian Regularization of a Low Dimensional Manifold Model

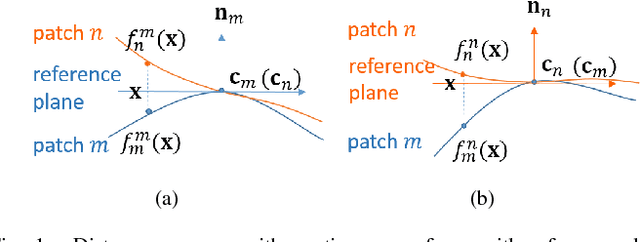
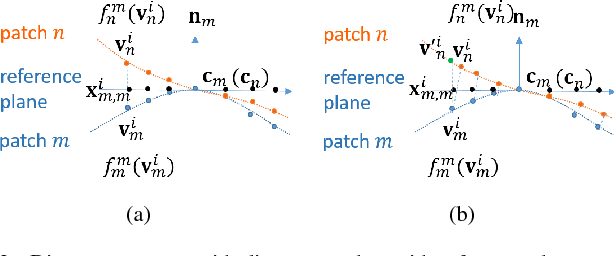
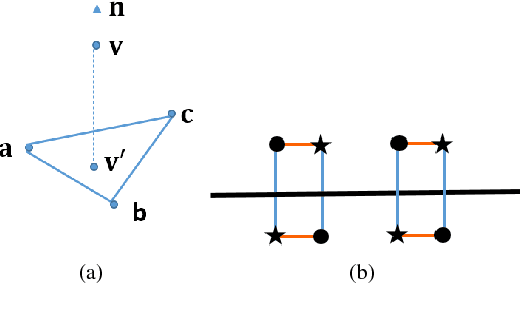
3D point cloud - a new signal representation of volumetric objects - is a discrete collection of triples marking exterior object surface locations in 3D space. Conventional imperfect acquisition processes of 3D point cloud - e.g., stereo-matching from multiple viewpoint images or depth data acquired directly from active light sensors - imply non-negligible noise in the data. In this paper, we adopt a previously proposed low-dimensional manifold model for the surface patches in the point cloud and seek self-similar patches to denoise them simultaneously using the patch manifold prior. Due to discrete observations of the patches on the manifold, we approximate the manifold dimension computation defined in the continuous domain with a patch-based graph Laplacian regularizer and propose a new discrete patch distance measure to quantify the similarity between two same-sized surface patches for graph construction that is robust to noise. We show that our graph Laplacian regularizer has a natural graph spectral interpretation, and has desirable numerical stability properties via eigenanalysis. Extensive simulation results show that our proposed denoising scheme can outperform state-of-the-art methods in objective metrics and can better preserve visually salient structural features like edges.