Safety Filters for Black-Box Dynamical Systems by Learning Discriminating Hyperplanes

Learning-based approaches are emerging as an effective approach for safety filters for black-box dynamical systems. Existing methods have relied on certificate functions like Control Barrier Functions (CBFs) and Hamilton-Jacobi (HJ) reachability value functions. The primary motivation for our work is the recognition that ultimately, enforcing the safety constraint as a control input constraint at each state is what matters. By focusing on this constraint, we can eliminate dependence on any specific certificate function-based design. To achieve this, we define a discriminating hyperplane that shapes the half-space constraint on control input at each state, serving as a sufficient condition for safety. This concept not only generalizes over traditional safety methods but also simplifies safety filter design by eliminating dependence on specific certificate functions. We present two strategies to learn the discriminating hyperplane: (a) a supervised learning approach, using pre-verified control invariant sets for labeling, and (b) a reinforcement learning (RL) approach, which does not require such labels. The main advantage of our method, unlike conventional safe RL approaches, is the separation of performance and safety. This offers a reusable safety filter for learning new tasks, avoiding the need to retrain from scratch. As such, we believe that the new notion of the discriminating hyperplane offers a more generalizable direction towards designing safety filters, encompassing and extending existing certificate-function-based or safe RL methodologies.

Constraint-Guided Online Data Selection for Scalable Data-Driven Safety Filters in Uncertain Robotic Systems

As the use of autonomous robotic systems expands in tasks that are complex and challenging to model, the demand for robust data-driven control methods that can certify safety and stability in uncertain conditions is increasing. However, the practical implementation of these methods often faces scalability issues due to the growing amount of data points with system complexity, and a significant reliance on high-quality training data. In response to these challenges, this study presents a scalable data-driven controller that efficiently identifies and infers from the most informative data points for implementing data-driven safety filters. Our approach is grounded in the integration of a model-based certificate function-based method and Gaussian Process (GP) regression, reinforced by a novel online data selection algorithm that reduces time complexity from quadratic to linear relative to dataset size. Empirical evidence, gathered from successful real-world cart-pole swing-up experiments and simulated locomotion of a five-link bipedal robot, demonstrates the efficacy of our approach. Our findings reveal that our efficient online data selection algorithm, which strategically selects key data points, enhances the practicality and efficiency of data-driven certifying filters in complex robotic systems, significantly mitigating scalability concerns inherent in nonparametric learning-based control methods.

Out of Distribution Detection via Domain-Informed Gaussian Process State Space Models

In order for robots to safely navigate in unseen scenarios using learning-based methods, it is important to accurately detect out-of-training-distribution (OoD) situations online. Recently, Gaussian process state-space models (GPSSMs) have proven useful to discriminate unexpected observations by comparing them against probabilistic predictions. However, the capability for the model to correctly distinguish between in- and out-of-training distribution observations hinges on the accuracy of these predictions, primarily affected by the class of functions the GPSSM kernel can represent. In this paper, we propose (i) a novel approach to embed existing domain knowledge in the kernel and (ii) an OoD online runtime monitor, based on receding-horizon predictions. Domain knowledge is provided in the form of a dataset, collected either in simulation or by using a nominal model. Numerical results show that the informed kernel yields better regression quality with smaller datasets, as compared to standard kernel choices. We demonstrate the effectiveness of the OoD monitor on a real quadruped navigating an indoor setting, which reliably classifies previously unseen terrains.

Stranding Risk for Underactuated Vessels in Complex Ocean Currents: Analysis and Controllers

Low-propulsion vessels can take advantage of powerful ocean currents to navigate towards a destination. Recent results demonstrated that vessels can reach their destination with high probability despite forecast errors. However, these results do not consider the critical aspect of safety of such vessels: because of their low propulsion which is much smaller than the magnitude of currents, they might end up in currents that inevitably push them into unsafe areas such as shallow areas, garbage patches, and shipping lanes. In this work, we first investigate the risk of stranding for free-floating vessels in the Northeast Pacific. We find that at least 5.04% would strand within 90 days. Next, we encode the unsafe sets as hard constraints into Hamilton-Jacobi Multi-Time Reachability (HJ-MTR) to synthesize a feedback policy that is equivalent to re-planning at each time step at low computational cost. While applying this policy closed-loop guarantees safe operation when the currents are known, in realistic situations only imperfect forecasts are available. We demonstrate the safety of our approach in such realistic situations empirically with large-scale simulations of a vessel navigating in high-risk regions in the Northeast Pacific. We find that applying our policy closed-loop with daily re-planning on new forecasts can ensure safety with high probability even under forecast errors that exceed the maximal propulsion. Our method significantly improves safety over the baselines and still achieves a timely arrival of the vessel at the destination.

Maximizing Seaweed Growth on Autonomous Farms: A Dynamic Programming Approach for Underactuated Systems Navigating on Uncertain Ocean Currents

Seaweed biomass offers significant potential for climate mitigation, but large-scale, autonomous open-ocean farms are required to fully exploit it. Such farms typically have low propulsion and are heavily influenced by ocean currents. We want to design a controller that maximizes seaweed growth over months by taking advantage of the non-linear time-varying ocean currents for reaching high-growth regions. The complex dynamics and underactuation make this challenging even when the currents are known. This is even harder when only short-term imperfect forecasts with increasing uncertainty are available. We propose a dynamic programming-based method to efficiently solve for the optimal growth value function when true currents are known. We additionally present three extensions when as in reality only forecasts are known: (1) our methods resulting value function can be used as feedback policy to obtain the growth-optimal control for all states and times, allowing closed-loop control equivalent to re-planning at every time step hence mitigating forecast errors, (2) a feedback policy for long-term optimal growth beyond forecast horizons using seasonal average current data as terminal reward, and (3) a discounted finite-time Dynamic Programming (DP) formulation to account for increasing ocean current estimate uncertainty. We evaluate our approach through 30-day simulations of floating seaweed farms in realistic Pacific Ocean current scenarios. Our method demonstrates an achievement of 95.8% of the best possible growth using only 5-day forecasts. This confirms the feasibility of using low-power propulsion and optimal control for enhanced seaweed growth on floating farms under real-world conditions.

Learning Players' Objectives in Continuous Dynamic Games from Partial State Observations

Robots deployed to the real world must be able to interact with other agents in their environment. Dynamic game theory provides a powerful mathematical framework for modeling scenarios in which agents have individual objectives and interactions evolve over time. However, a key limitation of such techniques is that they require a-priori knowledge of all players' objectives. In this work, we address this issue by proposing a novel method for learning players' objectives in continuous dynamic games from noise-corrupted, partial state observations. Our approach learns objectives by coupling the estimation of unknown cost parameters of each player with inference of unobserved states and inputs through Nash equilibrium constraints. By coupling past state estimates with future state predictions, our approach is amenable to simultaneous online learning and prediction in receding horizon fashion. We demonstrate our method in several simulated traffic scenarios in which we recover players' preferences for, e.g., desired travel speed and collision-avoidance behavior. Results show that our method reliably estimates game-theoretic models from noise-corrupted data that closely matches ground-truth objectives, consistently outperforming state-of-the-art approaches.

Generalized Optimality Guarantees for Solving Continuous Observation POMDPs through Particle Belief MDP Approximation

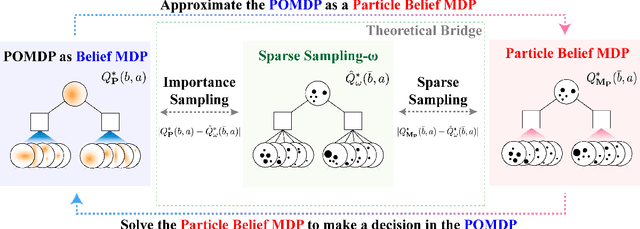
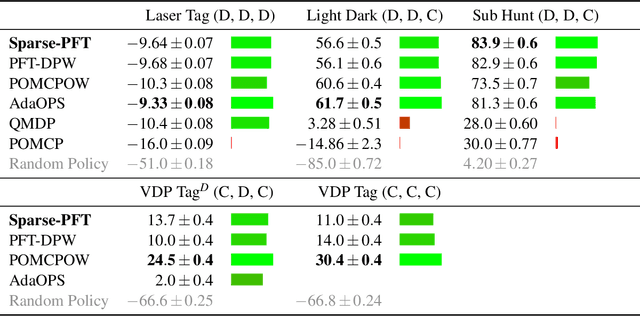
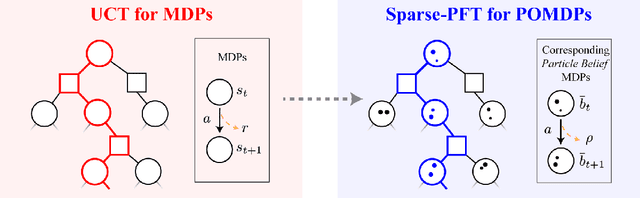
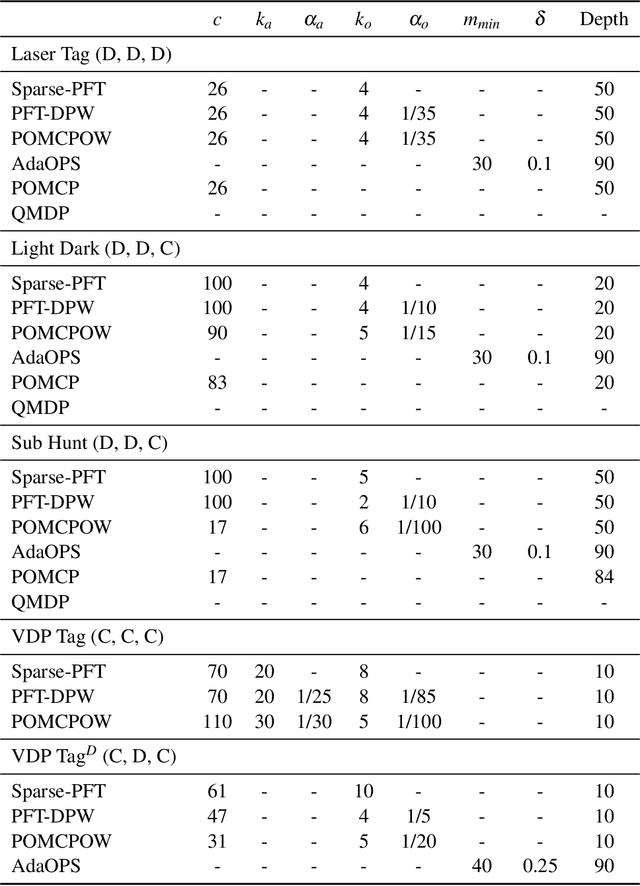
Partially observable Markov decision processes (POMDPs) provide a flexible representation for real-world decision and control problems. However, POMDPs are notoriously difficult to solve, especially when the state and observation spaces are continuous or hybrid, which is often the case for physical systems. While recent online sampling-based POMDP algorithms that plan with observation likelihood weighting have shown practical effectiveness, a general theory bounding the approximation error of the particle filtering techniques that these algorithms use has not previously been proposed. Our main contribution is to formally justify that optimality guarantees in a finite sample particle belief MDP (PB-MDP) approximation of a POMDP/belief MDP yields optimality guarantees in the original POMDP as well. This fundamental bridge between PB-MDPs and POMDPs allows us to adapt any sampling-based MDP algorithm of choice to a POMDP by solving the corresponding particle belief MDP approximation and preserve the convergence guarantees in the POMDP. Practically, this means additionally assuming access to the observation density model, and simply swapping out the state transition generative model with a particle filtering-based model, which only increases the computational complexity by a factor of $\mathcal{O}(C)$, with $C$ the number of particles in a particle belief state. In addition to our theoretical contribution, we perform five numerical experiments on benchmark POMDPs to demonstrate that a simple MDP algorithm adapted using PB-MDP approximation, Sparse-PFT, achieves performance competitive with other leading continuous observation POMDP solvers.

Probabilistic Safe Online Learning with Control Barrier Functions

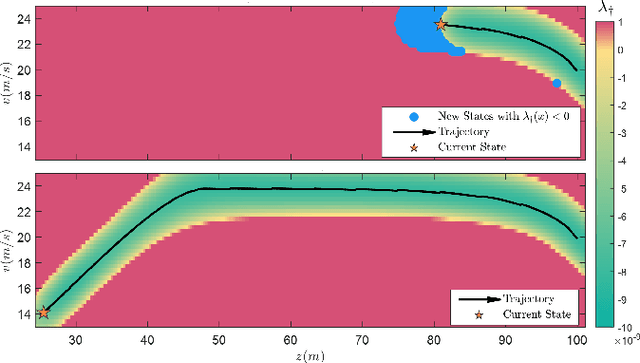
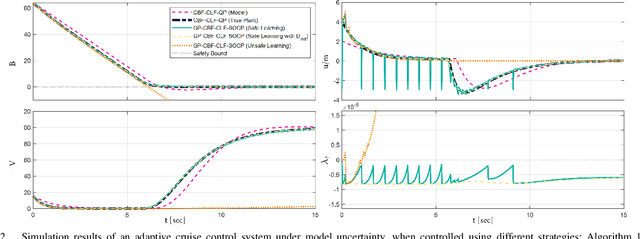
Learning-based control schemes have recently shown great efficacy performing complex tasks. However, in order to deploy them in real systems, it is of vital importance to guarantee that the system will remain safe during online training and execution. We therefore need safe online learning frameworks able to autonomously reason about whether the current information at their disposal is enough to ensure safety or, in contrast, new measurements are required. In this paper, we present a framework consisting of two parts: first, an out-of-distribution detection mechanism actively collecting measurements when needed to guarantee that at least one safety backup direction is always available for use; and second, a Gaussian Process-based probabilistic safety-critical controller that ensures the system stays safe at all times with high probability. Our method exploits model knowledge through the use of Control Barrier Functions, and collects measurements from the stream of online data in an event-triggered fashion to guarantee recursive feasibility of the learned safety-critical controller. This, in turn, allows us to provide formal results of forward invariance of a safe set with high probability, even in a priori unexplored regions. Finally, we validate the proposed framework in numerical simulations of an adaptive cruise control system.

Infinite-Horizon Reach-Avoid Zero-Sum Games via Deep Reinforcement Learning

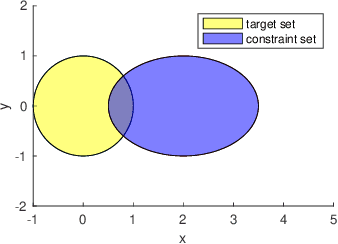
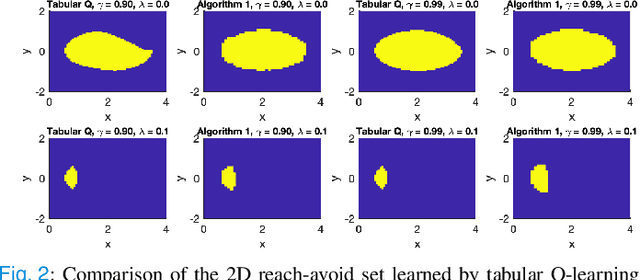
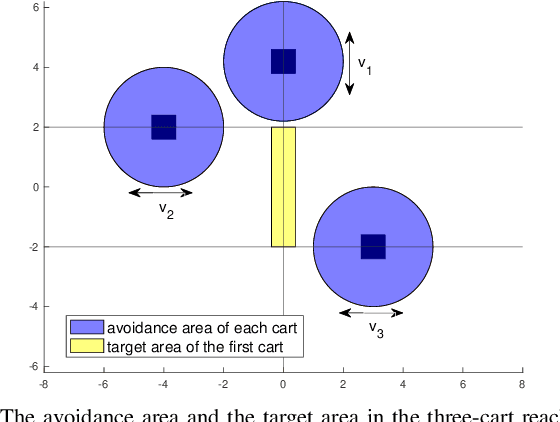
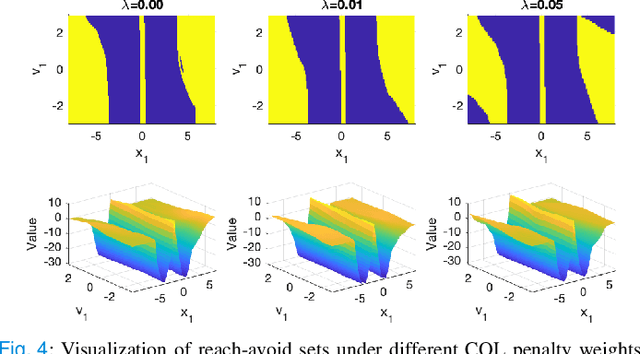
In this paper, we consider the infinite-horizon reach-avoid zero-sum game problem, where the goal is to find a set in the state space, referred to as the reach-avoid set, such that the system starting at a state therein could be controlled to reach a given target set without violating constraints under the worst-case disturbance. We address this problem by designing a new value function with a contracting Bellman backup, where the super-zero level set, i.e., the set of states where the value function is evaluated to be non-negative, recovers the reach-avoid set. Building upon this, we prove that the proposed method can be adapted to compute the viability kernel, or the set of states which could be controlled to satisfy given constraints, and the backward reachable set, or the set of states that could be driven towards a given target set. Finally, we propose to alleviate the curse of dimensionality issue in high-dimensional problems by extending Conservative Q-Learning, a deep reinforcement learning technique, to learn a value function such that the super-zero level set of the learned value function serves as a (conservative) approximation to the reach-avoid set. Our theoretical and empirical results suggest that the proposed method could learn reliably the reach-avoid set and the optimal control policy even with neural network approximation.

Computation of Regions of Attraction for Hybrid Limit Cycles Using Reachability: An Application to Walking Robots

Contact-rich robotic systems, such as legged robots and manipulators, are often represented as hybrid systems. However, the stability analysis and region-of-attraction computation for these systems are often challenging because of the discontinuous state changes upon contact (also referred to as state resets). In this work, we cast the computation of region-ofattraction as a Hamilton-Jacobi (HJ) reachability problem. This enables us to leverage HJ reachability tools that are compatible with general nonlinear system dynamics, and can formally deal with state and input constraints as well as bounded disturbances. Our main contribution is the generalization of HJ reachability framework to account for the discontinuous state changes originating from state resets, which has remained a challenge until now. We apply our approach for computing region-of-attractions for several underactuated walking robots and demonstrate that the proposed approach can (a) recover a bigger region-of-attraction than state-of-the-art approaches, (b) handle state resets, nonlinear dynamics, external disturbances, and input constraints, and (c) also provides a stabilizing controller for the system that can leverage the state resets for enhancing system stability.