OpenAI GPT-5 System Card

This is the system card published alongside the OpenAI GPT-5 launch, August 2025. GPT-5 is a unified system with a smart and fast model that answers most questions, a deeper reasoning model for harder problems, and a real-time router that quickly decides which model to use based on conversation type, complexity, tool needs, and explicit intent (for example, if you say 'think hard about this' in the prompt). The router is continuously trained on real signals, including when users switch models, preference rates for responses, and measured correctness, improving over time. Once usage limits are reached, a mini version of each model handles remaining queries. This system card focuses primarily on gpt-5-thinking and gpt-5-main, while evaluations for other models are available in the appendix. The GPT-5 system not only outperforms previous models on benchmarks and answers questions more quickly, but -- more importantly -- is more useful for real-world queries. We've made significant advances in reducing hallucinations, improving instruction following, and minimizing sycophancy, and have leveled up GPT-5's performance in three of ChatGPT's most common uses: writing, coding, and health. All of the GPT-5 models additionally feature safe-completions, our latest approach to safety training to prevent disallowed content. Similarly to ChatGPT agent, we have decided to treat gpt-5-thinking as High capability in the Biological and Chemical domain under our Preparedness Framework, activating the associated safeguards. While we do not have definitive evidence that this model could meaningfully help a novice to create severe biological harm -- our defined threshold for High capability -- we have chosen to take a precautionary approach.

Generative Data Mining with Longtail-Guided Diffusion

It is difficult to anticipate the myriad challenges that a predictive model will encounter once deployed. Common practice entails a reactive, cyclical approach: model deployment, data mining, and retraining. We instead develop a proactive longtail discovery process by imagining additional data during training. In particular, we develop general model-based longtail signals, including a differentiable, single forward pass formulation of epistemic uncertainty that does not impact model parameters or predictive performance but can flag rare or hard inputs. We leverage these signals as guidance to generate additional training data from a latent diffusion model in a process we call Longtail Guidance (LTG). Crucially, we can perform LTG without retraining the diffusion model or the predictive model, and we do not need to expose the predictive model to intermediate diffusion states. Data generated by LTG exhibit semantically meaningful variation, yield significant generalization improvements on image classification benchmarks, and can be analyzed to proactively discover, explain, and address conceptual gaps in a predictive model.

OpenAI o1 System Card

The o1 model series is trained with large-scale reinforcement learning to reason using chain of thought. These advanced reasoning capabilities provide new avenues for improving the safety and robustness of our models. In particular, our models can reason about our safety policies in context when responding to potentially unsafe prompts, through deliberative alignment. This leads to state-of-the-art performance on certain benchmarks for risks such as generating illicit advice, choosing stereotyped responses, and succumbing to known jailbreaks. Training models to incorporate a chain of thought before answering has the potential to unlock substantial benefits, while also increasing potential risks that stem from heightened intelligence. Our results underscore the need for building robust alignment methods, extensively stress-testing their efficacy, and maintaining meticulous risk management protocols. This report outlines the safety work carried out for the OpenAI o1 and OpenAI o1-mini models, including safety evaluations, external red teaming, and Preparedness Framework evaluations.

Key Algorithms for Keyphrase Generation: Instruction-Based LLMs for Russian Scientific Keyphrases

Keyphrase selection is a challenging task in natural language processing that has a wide range of applications. Adapting existing supervised and unsupervised solutions for the Russian language faces several limitations due to the rich morphology of Russian and the limited number of training datasets available. Recent studies conducted on English texts show that large language models (LLMs) successfully address the task of generating keyphrases. LLMs allow achieving impressive results without task-specific fine-tuning, using text prompts instead. In this work, we access the performance of prompt-based methods for generating keyphrases for Russian scientific abstracts. First, we compare the performance of zero-shot and few-shot prompt-based methods, fine-tuned models, and unsupervised methods. Then we assess strategies for selecting keyphrase examples in a few-shot setting. We present the outcomes of human evaluation of the generated keyphrases and analyze the strengths and weaknesses of the models through expert assessment. Our results suggest that prompt-based methods can outperform common baselines even using simple text prompts.

Compositional Sculpting of Iterative Generative Processes

High training costs of generative models and the need to fine-tune them for specific tasks have created a strong interest in model reuse and composition. A key challenge in composing iterative generative processes, such as GFlowNets and diffusion models, is that to realize the desired target distribution, all steps of the generative process need to be coordinated, and satisfy delicate balance conditions. In this work, we propose Compositional Sculpting: a general approach for defining compositions of iterative generative processes. We then introduce a method for sampling from these compositions built on classifier guidance. We showcase ways to accomplish compositional sculpting in both GFlowNets and diffusion models. We highlight two binary operations $\unicode{x2014}$ the harmonic mean ($p_1 \otimes p_2$) and the contrast ($p_1 \unicode{x25D1}\,p_2$) between pairs, and the generalization of these operations to multiple component distributions. We offer empirical results on image and molecular generation tasks.

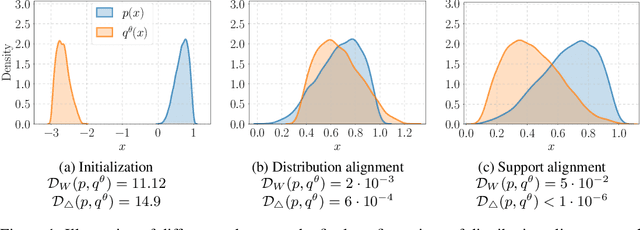
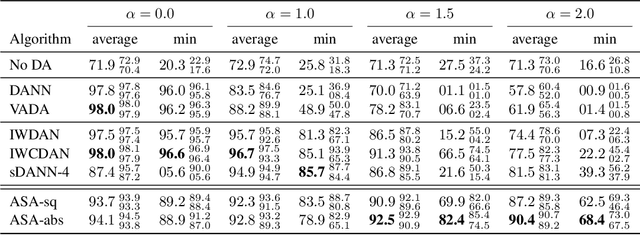
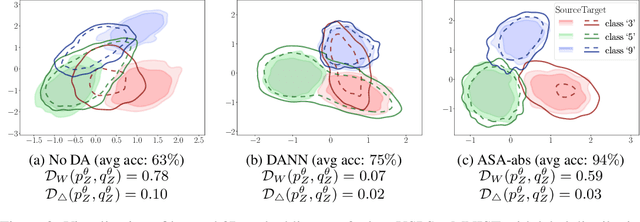
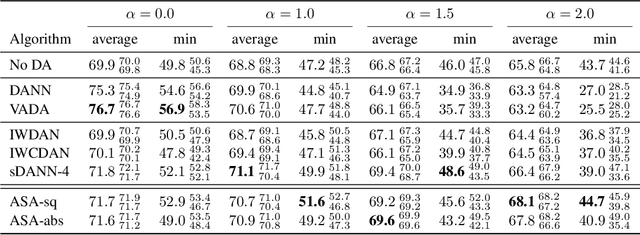
Adversarial Support Alignment

We study the problem of aligning the supports of distributions. Compared to the existing work on distribution alignment, support alignment does not require the densities to be matched. We propose symmetric support difference as a divergence measure to quantify the mismatch between supports. We show that select discriminators (e.g. discriminator trained for Jensen-Shannon divergence) are able to map support differences as support differences in their one-dimensional output space. Following this result, our method aligns supports by minimizing a symmetrized relaxed optimal transport cost in the discriminator 1D space via an adversarial process. Furthermore, we show that our approach can be viewed as a limit of existing notions of alignment by increasing transportation assignment tolerance. We quantitatively evaluate the method across domain adaptation tasks with shifts in label distributions. Our experiments show that the proposed method is more robust against these shifts than other alignment-based baselines.

The Benefits of Pairwise Discriminators for Adversarial Training

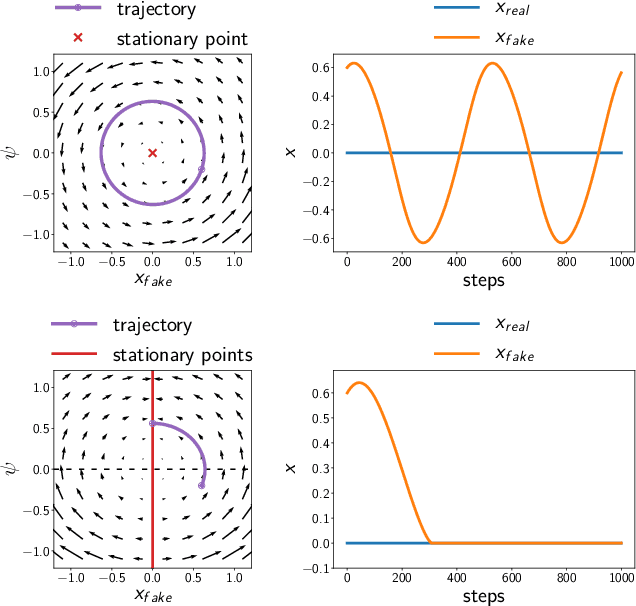
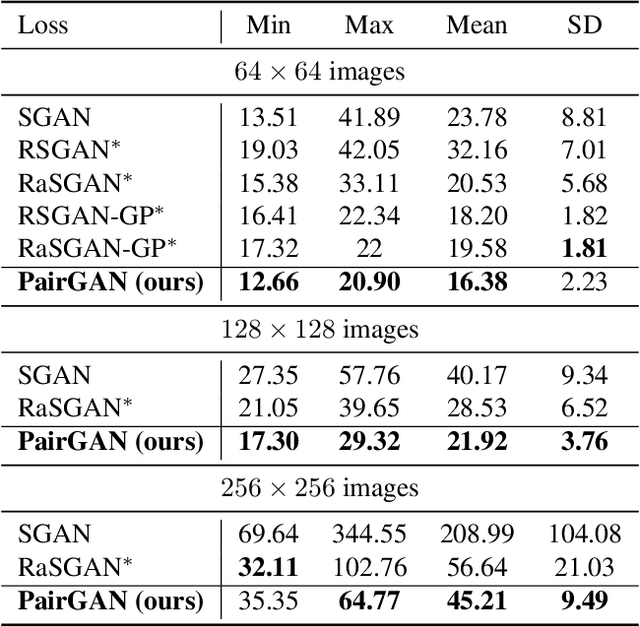
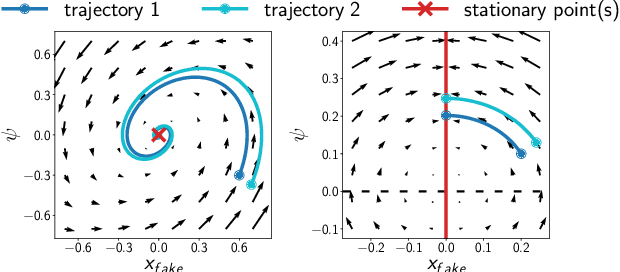
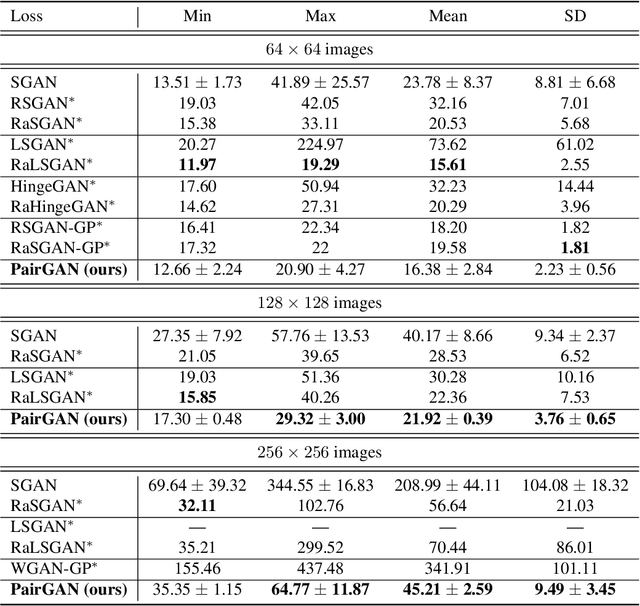
Adversarial training methods typically align distributions by solving two-player games. However, in most current formulations, even if the generator aligns perfectly with data, a sub-optimal discriminator can still drive the two apart. Absent additional regularization, the instability can manifest itself as a never-ending game. In this paper, we introduce a family of objectives by leveraging pairwise discriminators, and show that only the generator needs to converge. The alignment, if achieved, would be preserved with any discriminator. We provide sufficient conditions for local convergence; characterize the capacity balance that should guide the discriminator and generator choices; and construct examples of minimally sufficient discriminators. Empirically, we illustrate the theory and the effectiveness of our approach on synthetic examples. Moreover, we show that practical methods derived from our approach can better generate higher-resolution images.

MLRG Deep Curvature

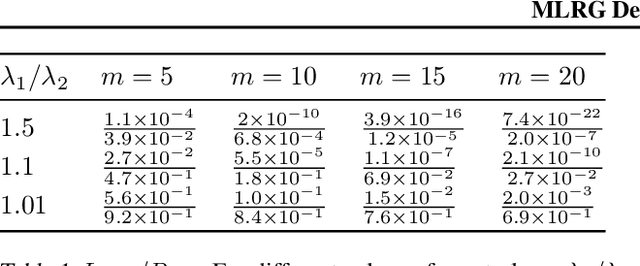
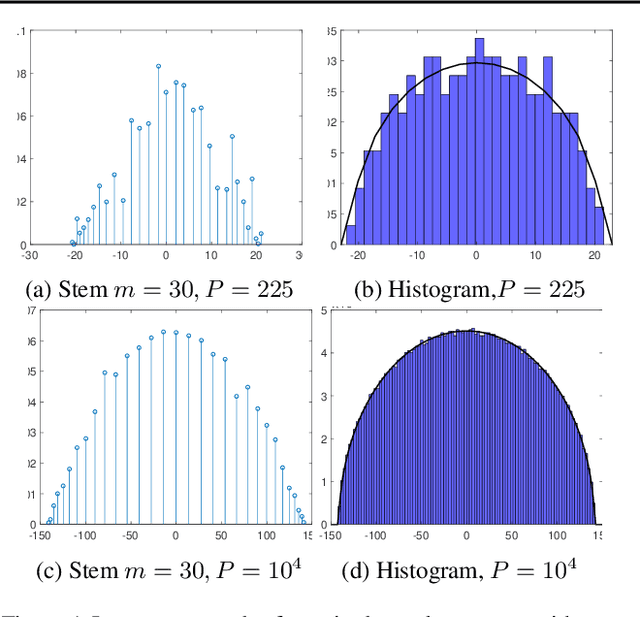
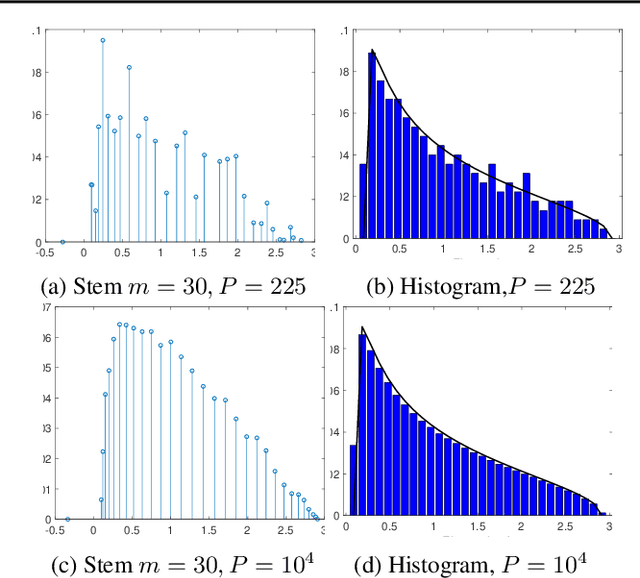
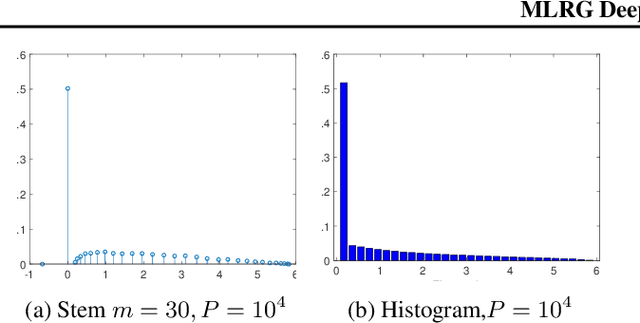
We present MLRG Deep Curvature suite, a PyTorch-based, open-source package for analysis and visualisation of neural network curvature and loss landscape. Despite of providing rich information into properties of neural network and useful for a various designed tasks, curvature information is still not made sufficient use for various reasons, and our method aims to bridge this gap. We present a primer, including its main practical desiderata and common misconceptions, of \textit{Lanczos algorithm}, the theoretical backbone of our package, and present a series of examples based on synthetic toy examples and realistic modern neural networks tested on CIFAR datasets, and show the superiority of our package against existing competing approaches for the similar purposes.

Subspace Inference for Bayesian Deep Learning

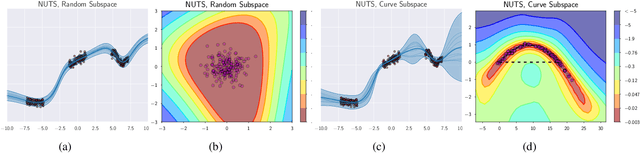
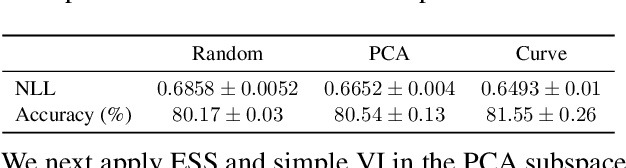
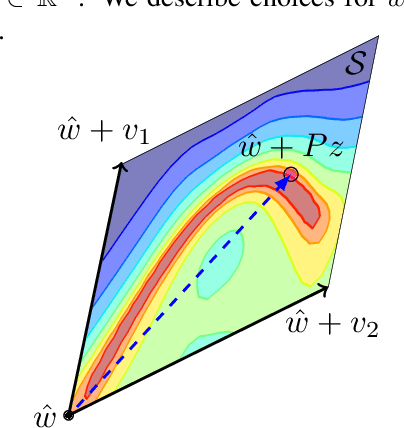
Bayesian inference was once a gold standard for learning with neural networks, providing accurate full predictive distributions and well calibrated uncertainty. However, scaling Bayesian inference techniques to deep neural networks is challenging due to the high dimensionality of the parameter space. In this paper, we construct low-dimensional subspaces of parameter space, such as the first principal components of the stochastic gradient descent (SGD) trajectory, which contain diverse sets of high performing models. In these subspaces, we are able to apply elliptical slice sampling and variational inference, which struggle in the full parameter space. We show that Bayesian model averaging over the induced posterior in these subspaces produces accurate predictions and well calibrated predictive uncertainty for both regression and image classification.

A Simple Baseline for Bayesian Uncertainty in Deep Learning

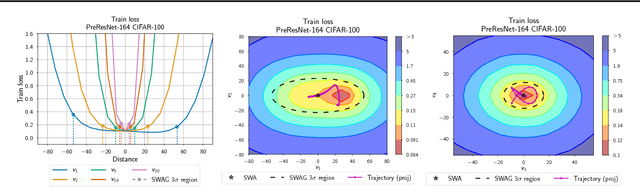
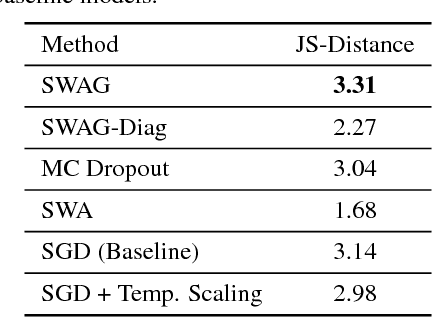
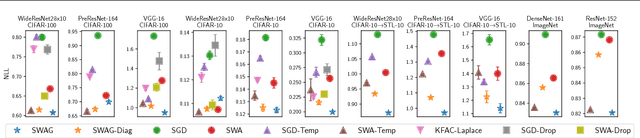
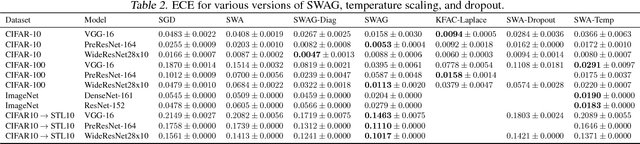
We propose SWA-Gaussian (SWAG), a simple, scalable, and general purpose approach for uncertainty representation and calibration in deep learning. Stochastic Weight Averaging (SWA), which computes the first moment of stochastic gradient descent (SGD) iterates with a modified learning rate schedule, has recently been shown to improve generalization in deep learning. With SWAG, we fit a Gaussian using the SWA solution as the first moment and a low rank plus diagonal covariance also derived from the SGD iterates, forming an approximate posterior distribution over neural network weights; we then sample from this Gaussian distribution to perform Bayesian model averaging. We empirically find that SWAG approximates the shape of the true posterior, in accordance with results describing the stationary distribution of SGD iterates. Moreover, we demonstrate that SWAG performs well on a wide variety of computer vision tasks, including out of sample detection, calibration, and transfer learning, in comparison to many popular alternatives including MC dropout, KFAC Laplace, and temperature scaling.