From Entropy to Epiplexity: Rethinking Information for Computationally Bounded Intelligence

Can we learn more from data than existed in the generating process itself? Can new and useful information be constructed from merely applying deterministic transformations to existing data? Can the learnable content in data be evaluated without considering a downstream task? On these questions, Shannon information and Kolmogorov complexity come up nearly empty-handed, in part because they assume observers with unlimited computational capacity and fail to target the useful information content. In this work, we identify and exemplify three seeming paradoxes in information theory: (1) information cannot be increased by deterministic transformations; (2) information is independent of the order of data; (3) likelihood modeling is merely distribution matching. To shed light on the tension between these results and modern practice, and to quantify the value of data, we introduce epiplexity, a formalization of information capturing what computationally bounded observers can learn from data. Epiplexity captures the structural content in data while excluding time-bounded entropy, the random unpredictable content exemplified by pseudorandom number generators and chaotic dynamical systems. With these concepts, we demonstrate how information can be created with computation, how it depends on the ordering of the data, and how likelihood modeling can produce more complex programs than present in the data generating process itself. We also present practical procedures to estimate epiplexity which we show capture differences across data sources, track with downstream performance, and highlight dataset interventions that improve out-of-distribution generalization. In contrast to principles of model selection, epiplexity provides a theoretical foundation for data selection, guiding how to select, generate, or transform data for learning systems.

A Unification of Discrete, Gaussian, and Simplicial Diffusion

To model discrete sequences such as DNA, proteins, and language using diffusion, practitioners must choose between three major methods: diffusion in discrete space, Gaussian diffusion in Euclidean space, or diffusion on the simplex. Despite their shared goal, these models have disparate algorithms, theoretical structures, and tradeoffs: discrete diffusion has the most natural domain, Gaussian diffusion has more mature algorithms, and diffusion on the simplex in principle combines the strengths of the other two but in practice suffers from a numerically unstable stochastic processes. Ideally we could see each of these models as instances of the same underlying framework, and enable practitioners to switch between models for downstream applications. However previous theories have only considered connections in special cases. Here we build a theory unifying all three methods of discrete diffusion as different parameterizations of the same underlying process: the Wright-Fisher population genetics model. In particular, we find simplicial and Gaussian diffusion as two large-population limits. Our theory formally connects the likelihoods and hyperparameters of these models and leverages decades of mathematical genetics literature to unlock stable simplicial diffusion. Finally, we relieve the practitioner of balancing model trade-offs by demonstrating it is possible to train a single model that can perform diffusion in any of these three domains at test time. Our experiments show that Wright-Fisher simplicial diffusion is more stable and outperforms previous simplicial diffusion models on conditional DNA generation. We also show that we can train models on multiple domains at once that are competitive with models trained on any individual domain.

The Forecast Critic: Leveraging Large Language Models for Poor Forecast Identification

Monitoring forecasting systems is critical for customer satisfaction, profitability, and operational efficiency in large-scale retail businesses. We propose The Forecast Critic, a system that leverages Large Language Models (LLMs) for automated forecast monitoring, taking advantage of their broad world knowledge and strong ``reasoning'' capabilities. As a prerequisite for this, we systematically evaluate the ability of LLMs to assess time series forecast quality, focusing on three key questions. (1) Can LLMs be deployed to perform forecast monitoring and identify obviously unreasonable forecasts? (2) Can LLMs effectively incorporate unstructured exogenous features to assess what a reasonable forecast looks like? (3) How does performance vary across model sizes and reasoning capabilities, measured across state-of-the-art LLMs? We present three experiments, including on both synthetic and real-world forecasting data. Our results show that LLMs can reliably detect and critique poor forecasts, such as those plagued by temporal misalignment, trend inconsistencies, and spike errors. The best-performing model we evaluated achieves an F1 score of 0.88, somewhat below human-level performance (F1 score: 0.97). We also demonstrate that multi-modal LLMs can effectively incorporate unstructured contextual signals to refine their assessment of the forecast. Models correctly identify missing or spurious promotional spikes when provided with historical context about past promotions (F1 score: 0.84). Lastly, we demonstrate that these techniques succeed in identifying inaccurate forecasts on the real-world M5 time series dataset, with unreasonable forecasts having an sCRPS at least 10% higher than that of reasonable forecasts. These findings suggest that LLMs, even without domain-specific fine-tuning, may provide a viable and scalable option for automated forecast monitoring and evaluation.

A Diffusion Model to Shrink Proteins While Maintaining Their Function

Many proteins useful in modern medicine or bioengineering are challenging to make in the lab, fuse with other proteins in cells, or deliver to tissues in the body, because their sequences are too long. Shortening these sequences typically involves costly, time-consuming experimental campaigns. Ideally, we could instead use modern models of massive databases of sequences from nature to learn how to propose shrunken proteins that resemble sequences found in nature. Unfortunately, these models struggle to efficiently search the combinatorial space of all deletions, and are not trained with inductive biases to learn how to delete. To address this gap, we propose SCISOR, a novel discrete diffusion model that deletes letters from sequences to generate protein samples that resemble those found in nature. To do so, SCISOR trains a de-noiser to reverse a forward noising process that adds random insertions to natural sequences. As a generative model, SCISOR fits evolutionary sequence data competitively with previous large models. In evaluation, SCISOR achieves state-of-the-art predictions of the functional effects of deletions on ProteinGym. Finally, we use the SCISOR de-noiser to shrink long protein sequences, and show that its suggested deletions result in significantly more realistic proteins and more often preserve functional motifs than previous models of evolutionary sequences.

Understanding the Implicit Biases of Design Choices for Time Series Foundation Models

Time series foundation models (TSFMs) are a class of potentially powerful, general-purpose tools for time series forecasting and related temporal tasks, but their behavior is strongly shaped by subtle inductive biases in their design. Rather than developing a new model and claiming that it is better than existing TSFMs, e.g., by winning on existing well-established benchmarks, our objective is to understand how the various ``knobs'' of the training process affect model quality. Using a mix of theory and controlled empirical evaluation, we identify several design choices (patch size, embedding choice, training objective, etc.) and show how they lead to implicit biases in fundamental model properties (temporal behavior, geometric structure, how aggressively or not the model regresses to the mean, etc.); and we show how these biases can be intuitive or very counterintuitive, depending on properties of the model and data. We also illustrate in a case study on outlier handling how multiple biases can interact in complex ways; and we discuss implications of our results for learning the bitter lesson and building TSFMs.

Efficiently Generating Correlated Sample Paths from Multi-step Time Series Foundation Models

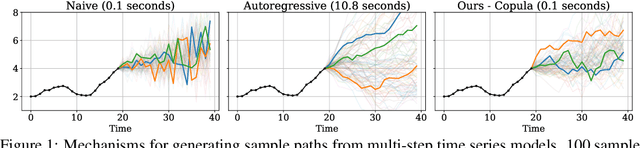
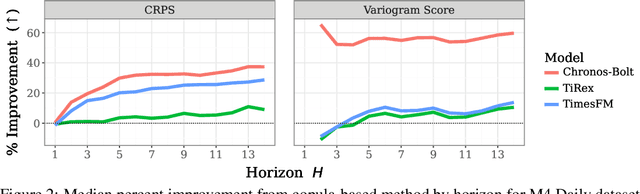
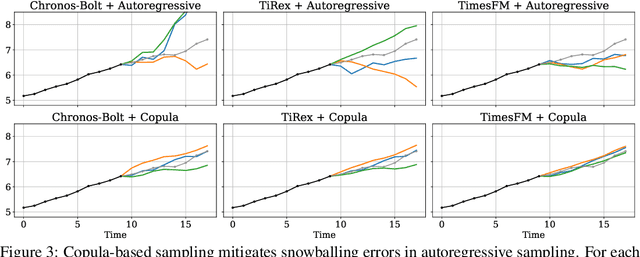
Many time series applications require access to multi-step forecast trajectories in the form of sample paths. Recently, time series foundation models have leveraged multi-step lookahead predictions to improve the quality and efficiency of multi-step forecasts. However, these models only predict independent marginal distributions for each time step, rather than a full joint predictive distribution. To generate forecast sample paths with realistic correlation structures, one typically resorts to autoregressive sampling, which can be extremely expensive. In this paper, we present a copula-based approach to efficiently generate accurate, correlated sample paths from existing multi-step time series foundation models in one forward pass. Our copula-based approach generates correlated sample paths orders of magnitude faster than autoregressive sampling, and it yields improved sample path quality by mitigating the snowballing error phenomenon.

Customizing the Inductive Biases of Softmax Attention using Structured Matrices

The core component of attention is the scoring function, which transforms the inputs into low-dimensional queries and keys and takes the dot product of each pair. While the low-dimensional projection improves efficiency, it causes information loss for certain tasks that have intrinsically high-dimensional inputs. Additionally, attention uses the same scoring function for all input pairs, without imposing a distance-dependent compute bias for neighboring tokens in the sequence. In this work, we address these shortcomings by proposing new scoring functions based on computationally efficient structured matrices with high ranks, including Block Tensor-Train (BTT) and Multi-Level Low Rank (MLR) matrices. On in-context regression tasks with high-dimensional inputs, our proposed scoring functions outperform standard attention for any fixed compute budget. On language modeling, a task that exhibits locality patterns, our MLR-based attention method achieves improved scaling laws compared to both standard attention and variants of sliding window attention. Additionally, we show that both BTT and MLR fall under a broader family of efficient structured matrices capable of encoding either full-rank or distance-dependent compute biases, thereby addressing significant shortcomings of standard attention. Finally, we show that MLR attention has promising results for long-range time-series forecasting.

Small Batch Size Training for Language Models: When Vanilla SGD Works, and Why Gradient Accumulation Is Wasteful

Conventional wisdom dictates that small batch sizes make language model pretraining and fine-tuning unstable, motivating gradient accumulation, which trades off the number of optimizer steps for a proportional increase in batch size. While it is common to decrease the learning rate for smaller batch sizes, other hyperparameters are often held fixed. In this work, we revisit small batch sizes all the way down to batch size one, and we propose a rule for scaling Adam hyperparameters to small batch sizes. We find that small batch sizes (1) train stably, (2) are consistently more robust to hyperparameter choices, (3) achieve equal or better per-FLOP performance than larger batch sizes, and (4) notably enable stable language model training with vanilla SGD, even without momentum, despite storing no optimizer state. Building on these results, we provide practical recommendations for selecting a batch size and setting optimizer hyperparameters. We further recommend against gradient accumulation unless training on multiple devices with multiple model replicas, bottlenecked by inter-device bandwidth.

Scaling Collapse Reveals Universal Dynamics in Compute-Optimally Trained Neural Networks

What scaling limits govern neural network training dynamics when model size and training time grow in tandem? We show that despite the complex interactions between architecture, training algorithms, and data, compute-optimally trained models exhibit a remarkably precise universality. Specifically, loss curves from models of varying sizes collapse onto a single universal curve when training compute and loss are normalized to unity at the end of training. With learning rate decay, the collapse becomes so tight that differences in the normalized curves across models fall below the noise floor of individual loss curves across random seeds, a phenomenon we term supercollapse. We observe supercollapse across learning rate schedules, datasets, and architectures, including transformers trained on next-token prediction, and find it breaks down when hyperparameters are scaled suboptimally, providing a precise and practical indicator of good scaling. We explain these phenomena by connecting collapse to the power-law structure in typical neural scaling laws, and analyzing a simple yet surprisingly effective model of SGD noise dynamics that accurately predicts loss curves across various learning rate schedules and quantitatively explains the origin of supercollapse.

Out-of-Distribution Detection Methods Answer the Wrong Questions

To detect distribution shifts and improve model safety, many out-of-distribution (OOD) detection methods rely on the predictive uncertainty or features of supervised models trained on in-distribution data. In this paper, we critically re-examine this popular family of OOD detection procedures, and we argue that these methods are fundamentally answering the wrong questions for OOD detection. There is no simple fix to this misalignment, since a classifier trained only on in-distribution classes cannot be expected to identify OOD points; for instance, a cat-dog classifier may confidently misclassify an airplane if it contains features that distinguish cats from dogs, despite generally appearing nothing alike. We find that uncertainty-based methods incorrectly conflate high uncertainty with being OOD, while feature-based methods incorrectly conflate far feature-space distance with being OOD. We show how these pathologies manifest as irreducible errors in OOD detection and identify common settings where these methods are ineffective. Additionally, interventions to improve OOD detection such as feature-logit hybrid methods, scaling of model and data size, epistemic uncertainty representation, and outlier exposure also fail to address this fundamental misalignment in objectives. We additionally consider unsupervised density estimation and generative models for OOD detection, which we show have their own fundamental limitations.